Converting Between Denary & Hexadecimal (OCR GCSE Computer Science)

Denary to Hexadecimal Conversion

What is hexadecimal?

• Hexadecimal is a number system that is made up of 16 digits, 10 numbers (0-9) and 6 letters (A-F)

• Hexadecimal is referred to as a Base-16 number system

• Each digit has a weight factor of 16 raised to a power, the rightmost digit is 1s (16^0), the next digit to the left 16s (16^1)

• In GCSE you are required to work with up to and including 2 digit hexadecimal values

• A quick comparison table demonstrates a relationship between hexadecimal and a binary nibble 

• One hexadecimal digit can represent four bits of binary data

Why is hexadecimal used?

• In Computer Science hexadecimal is often preferred when working with large values

• It takes fewer digits to represent a given value in hexadecimal than in binary

• It is beneficial to use hexadecimal over binary because:

  • The more bits there are in a binary number, the harder it is to read

  • Numbers with more bits are more prone to errors when being copied

• Examples of where hexadecimal can be seen:

  • MAC addresses

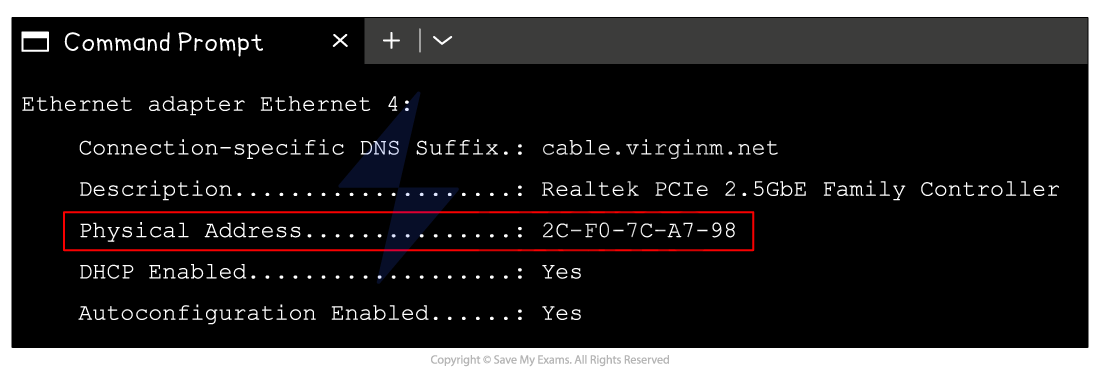
• Colour values

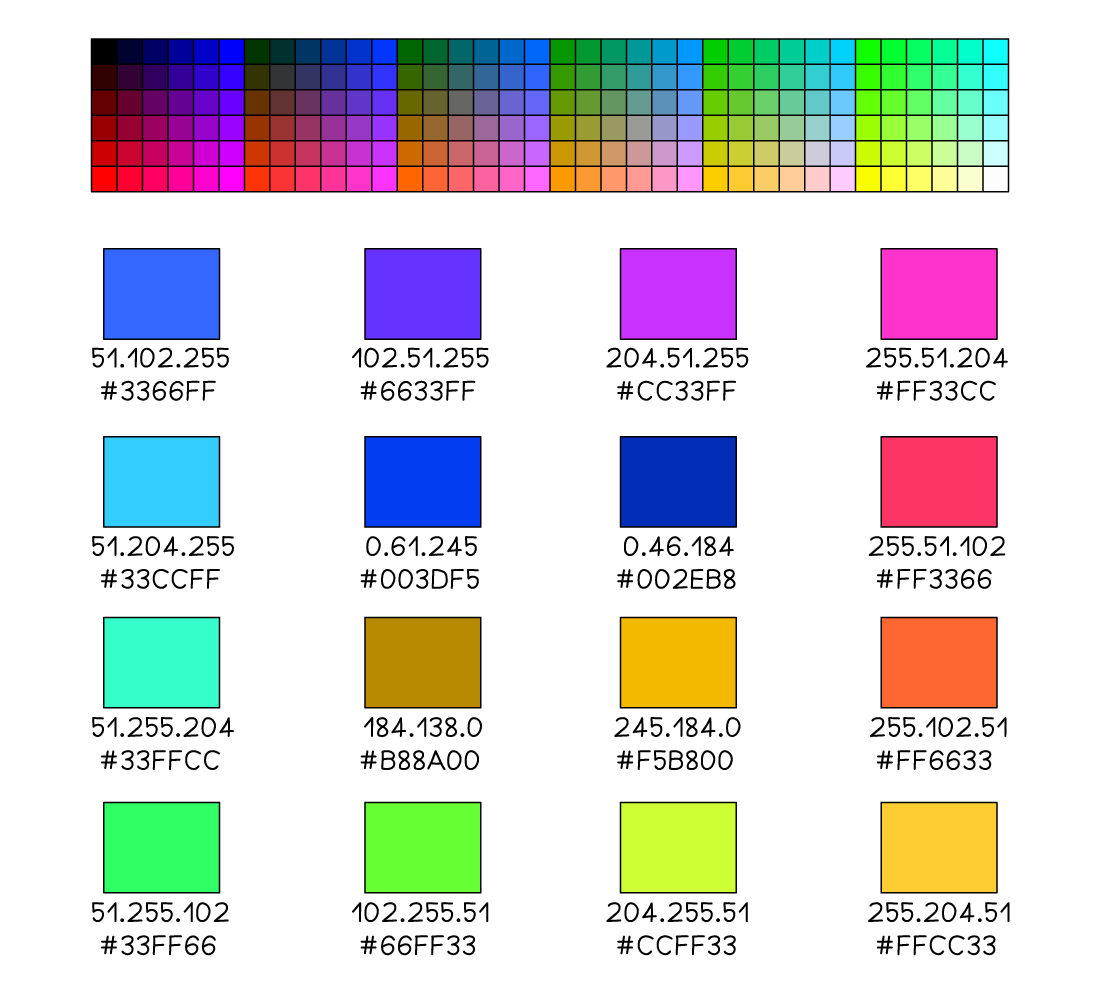
How do you convert denary to hexadecimal?

Method 1 (denary to binary to hexadecimal) 

• To convert the denary number 28 to hexadecimal, start by converting the denary number to binary

• Split the 8 bit binary number into two nibbles as shown below

• Convert each nibble to its denary value

• 0001 = 1 and 1100 = 12

• Using the comparison table, the denary value 1 is also 1 in hexadecimal whereas denary value 12 is represented in hexadecimal as C

• Denary 28 is 1C in hexadecimal

Method 2 (divide by 16)

• To convert the denary number 163 to hexadecimal, start by dividing the denary value by 16 and recording the whole times the number goes in and the remainder

• 163 16 = 10 remainder 3

• In hexadecimal the whole number = digit 1 and the remainder = digit 2

• Digit 1 = 10 (A)

• Digit 2 = 3

• Denary 163 is A3 in hexadecimal

Hexadecimal to Denary Conversion

How do you convert hexadecimal to denary?

Method 1 (hexadecimal to binary to denary)

• To convert the hexadecimal number B9 to denary, take each hexadecimal value and convert it as denary to 4 bit binary

• Join the two nibbles to make an 8 bit number (byte)

• Convert from binary to denary

• (1 x 128) + (1 x 32) + (1 x 16) + (1 x 8) + (1 x 1) = 185

• Hexadecimal B9 is 185 in denary

Method 2 (multiply by 16)

• To convert the hexadecimal number 79 to denary, start by multiplying the first hexadecimal digit by 16

• 7 16 = 112

• Add digit 2 to the result

• 112 + 9 = 121

• Hexadecimal 79 is 121 in denary