Converting Between Hexadecimal & Binary (Edexcel GCSE Computer Science): Revision Note
Exam code: 1CP2
The Use of Hexadecimal in Computing
Why is hexadecimal used?
In Computer Science hexadecimal is often preferred when working with large values
It takes fewer digits to represent a given value in hexadecimal than in binary
1 hexadecimal digit corresponds 4 bits (one nibble) and can represent 16 unique values (0-F)
It is beneficial to use hexadecimal over binary because:
The more bits there are in a binary number, the harder it makes for a human to read
Numbers with more bits are more prone to errors when being copied
Examples of where hexadecimal can be seen:
MAC addresses
Colour values
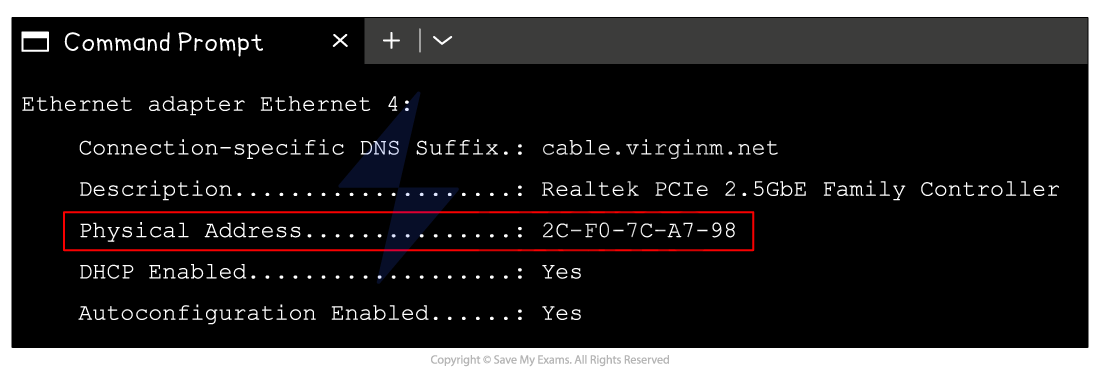
A typical MAC address consists of 12 hexadecimal digits, equivalent to 48 digits in in binary
AA:BB:CC:DD:EE:FF
10101010:10111011:11001100:11011101:11101110:11111111
Writing down or performing calculations with 48 binary digits makes it very easy to make a mistake
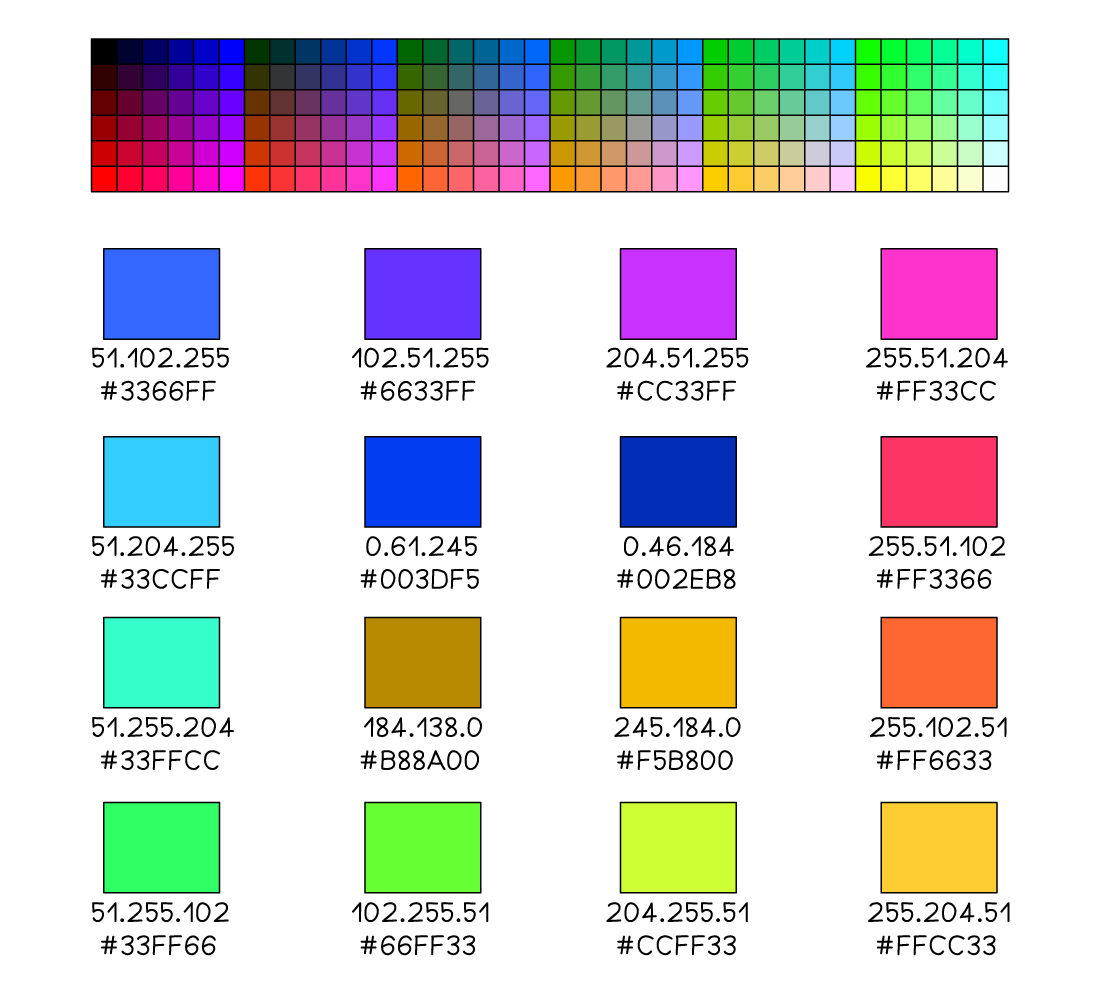
A typical hexadecimal colour code consists of 6 hexadecimal digits, equivalent to 24 digits in binary
#66FF33 (green)
01000010:11111111:00110011
Hexadecimal to Binary Conversion
How do you convert from hexadecimal to binary?
Example 1
To convert the hexadecimal number 5F to binary, first split the digits apart and convert each to a binary nibble (4 bits)
8 | 4 | 2 | 1 |
|
|---|---|---|---|---|
0 | 1 | 0 | 1 | = 5 |
8 | 4 | 2 | 1 |
|
|---|---|---|---|---|
1 | 1 | 1 | 1 | = 15 (F) |
Join the 2 binary nibbles together to create an 8 bit binary number
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
Hexadecimal 5F is 01011111 in binary
Example 2
To convert the hexadecimal number 26 to binary, first split the digits apart and convert each to a binary nibble (4 bits)
8 | 4 | 2 | 1 |
|
|---|---|---|---|---|
0 | 0 | 1 | 0 | = 2 |
8 | 4 | 2 | 1 |
|
|---|---|---|---|---|
0 | 1 | 1 | 0 | = 6 |
Join the 2 binary nibbles together to create an 8 bit binary number
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
Hexadecimal 26 is 00100110 in binary
Binary to Hexadecimal Conversion
How do you convert from binary to hexadecimal?
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Example 1
To convert the binary number 10110111 to hexadecimal, first split the 8 bit number into 2 binary nibbles
8 | 4 | 2 | 1 |
| 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
For each nibble, convert the binary to it’s denary value
(1 x 8) + (1 x 2) + (1 x 1) = 11 (B)
(1 x 4) + (1 x 2) + (1 x 1) = 7
Join them together to make a 2 digit hexadecimal number
Binary 10110111 is B7 in hexadecimal
Example 2
To convert the binary number 00111001 to hexadecimal, first split the 8 bit number into 2 binary nibbles
8 | 4 | 2 | 1 |
| 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 |
For each nibble, convert the binary to it’s denary value
(1 x 2) + (1 x 1) = 3
(1 x 8) + (1 x 1) = 9
Join them together to make a 2 digit hexadecimal number
Binary 00111001 is 39 in hexadecimal

Unlock more, it's free!
Did this page help you?