Binary Addition (Edexcel GCSE Computer Science): Revision Note
Exam code: 1CP2
Binary Addition
What is binary addition?
Binary addition is the process of adding together two binary integers (up to and including 8 bits)
To be successful there are 5 golden rules to apply:
Binary Addition | Binary Answer | Working | ||||||
|---|---|---|---|---|---|---|---|---|
0 + 0 = | 0 |
| ||||||
0 + 1 = | 1 |
| ||||||
1 + 0 = | 1 |
| ||||||
1 + 1 = | 10 |
| ||||||
1 + 1 + 1 = | 11 |
|
Like denary addition, start from the rightmost digit and move left
Carrying over occurs when the sum of a column is greater than 1, passing the excess to the next left column
Example 1
Add together the binary values 1001 and 0100
8 | 4 | 2 | 1 | + |
|---|---|---|---|---|
1 | 0 | 0 | 1 | |
0 | 1 | 0 | 0 | |
|
|
|
| C |
|
|
|
|
|
Starting from right to left, add the two binary values together applying the 5 golden rules
If your answer has 2 digits, place the rightmost digit in the column and carry the remaining digit to the next column on the left
In this example, start with 1+0, 1+0 = 1, so place a 1 in the column
8 | 4 | 2 | 1 | + |
|---|---|---|---|---|
1 | 0 | 0 | 1 | |
0 | 1 | 0 | 0 | |
|
|
|
| C |
|
|
| 1 |
|
Repeat until all columns have a value
8 | 4 | 2 | 1 | + |
|---|---|---|---|---|
1 | 0 | 0 | 1 | |
0 | 1 | 0 | 0 | |
|
|
|
| C |
1 | 1 | 0 | 1 |
|
The sum of adding together binary 1001 (9) and 0100 (4) is 1101 (13)
Examiner Tips and Tricks
Make sure any carried digits are clearly visible in your answer, there are marks available for working. Carries can be put above or below in the addition
Example 2
Add together the binary values 00011001 and 10000100
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | + |
|---|---|---|---|---|---|---|---|---|
0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |
1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
|
|
|
|
|
|
|
| C |
|
|
|
|
|
|
|
|
|
Starting from right to left, add the two binary values together applying the 5 golden rules
If your answer has 2 digits, place the rightmost digit in the column and carry the remaining digit to the next column on the left
In this example, start with 1+1, 1+1 = 10, so place a 0 in the column and carry the 1 to the next column
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | + |
|---|---|---|---|---|---|---|---|---|
0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |
1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
|
|
|
|
|
| 1 |
| C |
|
|
|
|
|
|
| 0 |
|
Repeat until all columns have a value
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | + |
|---|---|---|---|---|---|---|---|---|
0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |
1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
|
| 1 | 1 |
|
| 1 |
| C |
1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
|
The sum of adding together binary 00011001 (25) and 10001001 (137) is 10100010 (162)
Overflows
What is an overflow error?
An overflow error occurs when the result of a binary addition exceeds the available bits
For example, if you took binary 11111111 (255) and tried to add 00000001 (1) this would cause an overflow error as the result would need a 9th bit to represent the answer (256)
256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | + |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| C |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
Examiner Tips and Tricks
When starting a binary addition question, always look at the question that comes after. If it asks you to name what problem has been caused, you know the binary addition question must cause an overflow error and therefore mean a carried bit that does not fit in to the answer
Binary Shifts
What is a logical binary shift?
A logical binary shift is how a computer system performs basic multiplication and division on unsigned binary integers
Binary digits are moved left or right a set number of times
A left shift multiplies a binary number by 2 (x2)
A right shift divides a binary number by 2 (/2)
A shift can move more than one place at a time, the principle remains the same
A left shift of 2 places would multiply the original binary number by 4 (x4)
How do you perform a logical left shift of 1?
Here is the binary representation of the denary number 40
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
To perform a left logical binary shift of 1, we move each bit 1 place to the left
The digit in the 128 column (MSB) will move left causing an overflow error
The 1 column becomes empty so is filled with a 0
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|
|---|---|---|---|---|---|---|---|---|
0 | 1 | 0 | 1 | 0 | 0 | 0 | = 40 | |
0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | = 80 |
The original binary representation of denary 40 (32+8) has multiplied by 2 and became 80 (64+16)
How do you perform a logical left shift of 2?
Here is the binary representation of the denary number 28
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
To perform a left binary shift of 2, we move each bit 2 place to the left
The digit in the 128 (MSB) and 64 column will move left causing an overflow error
The 1 and 2 column become empty so are filled with a 0
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|
|---|---|---|---|---|---|---|---|---|
0 | 1 | 1 | 1 | 0 | 0 | = 28 | ||
0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | = 112 |
The original binary representation of denary 28 (16+8+4) has multiplied by 4 and became 112 (64+32+16)
How do you perform a logical right shift of 1?
Here is the binary representation of the denary number 40
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
To perform a right binary shift of 1, we move each bit 1 place to the right
The digit in the 1 column (LSB) will move right causing an underflow error
The 128 column becomes empty so is filled with a 0
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|
|---|---|---|---|---|---|---|---|---|
0 | 0 | 1 | 0 | 1 | 0 | 0 | = 40 | |
0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | = 20 |
The original binary representation of denary 40 (32+8) has divided by 2 and became 20 (16+4)
How do you perform a logical right shift of 2?
Here is the binary representation of the denary number 200
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
To perform a right binary shift of 2, we move each bit 2 places to the right
The digits in the 1 (LSB) and 2 columns will move right causing an underflow error
The 128 and 64 columns become empty so are filled with a 0
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|
|---|---|---|---|---|---|---|---|---|
1 | 1 | 0 | 0 | 1 | 0 | = 200 | ||
0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | = 50 |
The original binary representation of denary 200 (128+64+8) has divided by 4 and became 50 (32+16+2)
What is an arithmetic binary shift?
An arithmetic binary shift is used to divide signed binary integers by moving bits right
Multiplication on signed binary integers by moving bits left can not be completed because the MSB is not preserved
Example
Take the 8 bit signed binary integer
-128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|
|---|---|---|---|---|---|---|---|---|
1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | = -125 |
Using a logical binary shift of 1 place right would mean the MSB moves 1 place right, leaving an empty space to be filled with a 0, changing the value from negative to positive
This results in a lack of precision and is why this method cannot be used
In order to successfully complete the right shift, an arithmetic binary shift should be used
As with a logical binary shift all bits move to the right, except, the MSB after moving is copied back to it's original state
-128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|
|---|---|---|---|---|---|---|---|---|
1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | = -63 |
In this example an arithmetic binary shift of 1 place right would convert -125 to -63
Worked Example
1. Perform a logical binary shift of 2 places left on the binary number 00001110 [1]
2. Explain the effect of performing a 2 place shift to the left on the binary number 00001110 [2]
Answers
Q1
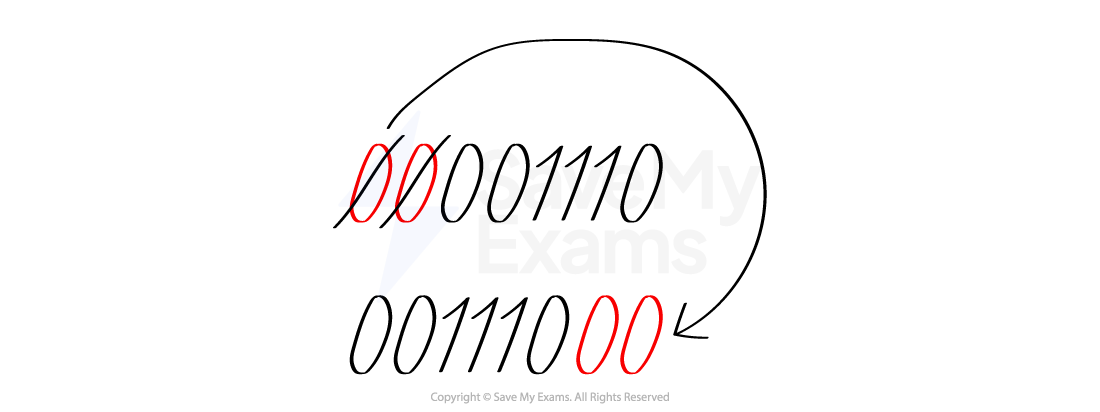
Cross out the first 2 digits from the left
Write down the binary digits left and add 2 zeros to the end
Q2
Multiplies the number by 4
Overflow errors can cause loss of precision

Unlock more, it's free!
Did this page help you?