Binary Shifts (AQA GCSE Computer Science) : Revision Note
Binary Shifts
What is a binary shift?
A binary shift is how a computer system performs basic multiplication and division
Binary digits are moved left or right a set number of times
A left shift multiplies a binary number by 2 (x2)
A right shift divides a binary number by 2 (/2)
A shift can move more than one place at a time, the principle remains the same
A left shift of 2 places would multiply the original binary number by 4 (x4)
How do you perform a left shift of 1?
Here is the binary representation of the denary number 40

To perform a left binary shift of 1, we move each bit 1 place to the left
The digit in the 128 column will move left causing an overflow error
The 1 column becomes empty so is filled with a 0

The original binary representation of denary 40 (32+8) has multiplied by 2 and became 80 (64+16)
How do you perform a left shift of 2?
Here is the binary representation of the denary number 28

To perform a left binary shift of 2, we move each bit 2 place to the left
The digit in the 128 and 64 column will move left causing an overflow error
The 1 and 2 column become empty so are filled with a 0

The original binary representation of denary 28 (16+8+4) has multiplied by 4 and became 112 (64+32+16)
How do you perform a right shift of 1?
Here is the binary representation of the denary number 40

To perform a right binary shift of 1, we move each bit 1 place to the right
The digit in the 1 column will move right causing an underflow error
The 128 column becomes empty so is filled with a 0

The original binary representation of denary 40 (32+8) has divided by 2 and became 20 (16+4)
How do you perform a right shift of 2?
Here is the binary representation of the denary number 200

To perform a right binary shift of 2, we move each bit 2 places to the right
The digits in the 1 and 2 columns will move right causing an underflow error
The 128 and 64 columns become empty so are filled with a 0

The original binary representation of denary 200 (128+64+8) has divided by 4 and became 50 (32+16+2)
Worked Example
1. Perform a binary shift of 2 places left on the binary number 00001110 [1]
2. Explain the effect of performing a 2 place shift to the left on the binary number 00001110 [2]
Answers
Q1
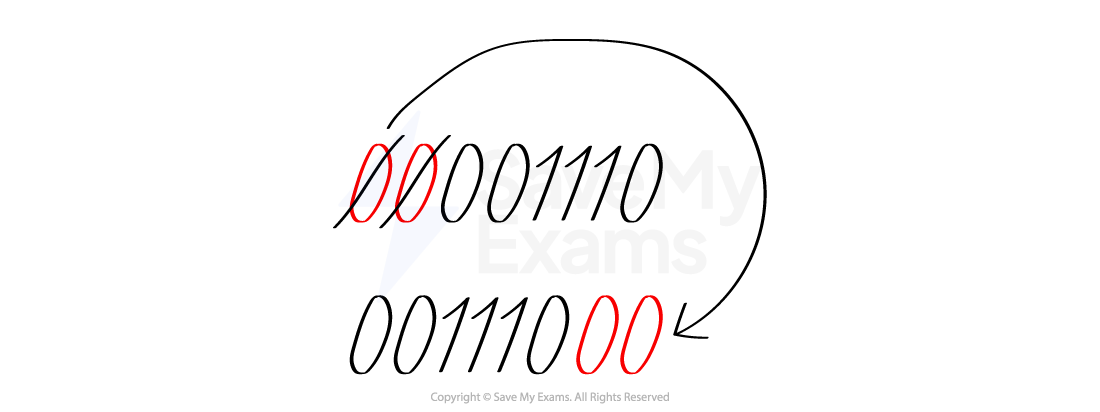
Cross out the first 2 digits from the left
Write down the binary digits left and add 2 zeros to the end
Q2
Multiplies the number by 4
Overflow errors can cause loss of precision

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

