Binary Addition (AQA GCSE Computer Science)

Binary Addition

What is binary addition?

• Binary addition is the process of adding together up to three binary integers (up to and including 8 bits)

• To be successful there are 5 golden rules to apply:

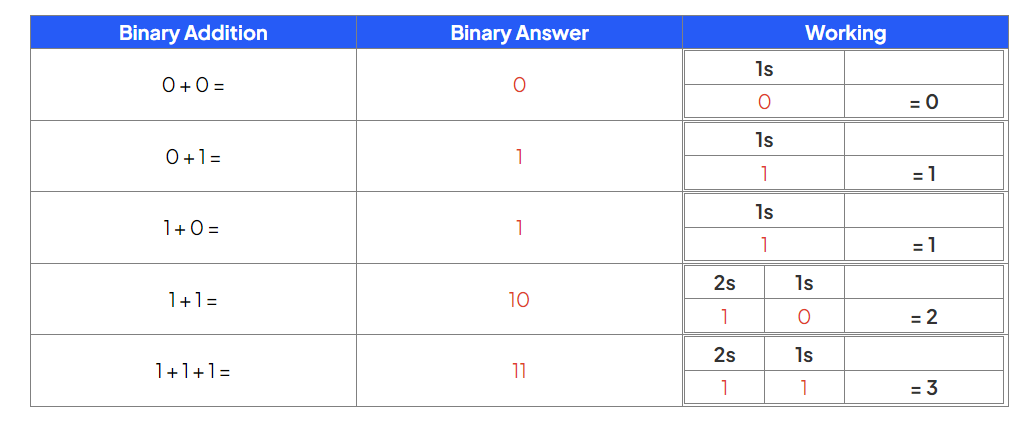
• Like denary addition, start from the rightmost digit and move left

• Carrying over occurs when the sum of a column is greater than 1, passing the excess to the next left column

Example 1

• Add together the binary values 1001 and 0100

• Starting from right to left, add the two binary values together applying the 5 golden rules

• If your answer has 2 digits, place the rightmost digit in the column and carry the remaining digit to the next column on the left

• In this example, start with 1+0, 1+0 = 1, so place a 1 in the column

• Repeat until all columns have a value

• The sum of adding together binary 1001 (9) and 0100 (4) is 1101 (13)

Example 2

• Add together the binary values 00011001 and 10000100

• Starting from right to left, add the two binary values together applying the 5 golden rules

• If your answer has 2 digits, place the rightmost digit in the column and carry the remaining digit to the next column on the left

• In this example, start with 1+1, 1+1 = 10, so place a 0 in the column and carry the 1 to the next column

• Repeat until all columns have a value

• The sum of adding together binary 00011001 (25) and 10001001 (137) is 10100010 (162)

Example 3

• Add together the binary values 00011011, 00010110 and 00100010

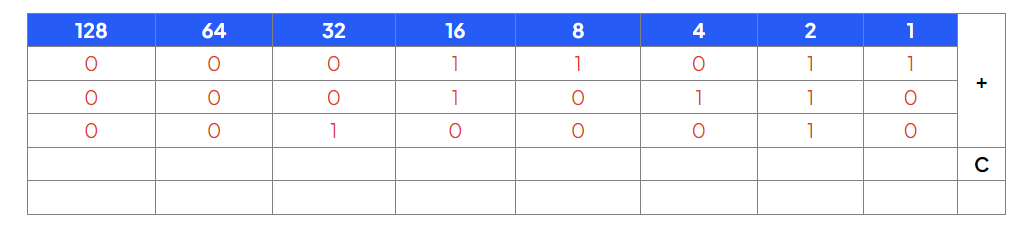
• Starting from right to left, add the two binary values together applying the 5 golden rules

• If your answer has 2 digits, place the rightmost digit in the column and carry the remaining digit to the next column on the left

• In this example, start with 1+0+0, 1+0+0 = 1, so place a 1 in the column

• In the second column we have 1+1+1, 1+1+1 = 11, so place 1 in that column and carry the other 1 to the next column

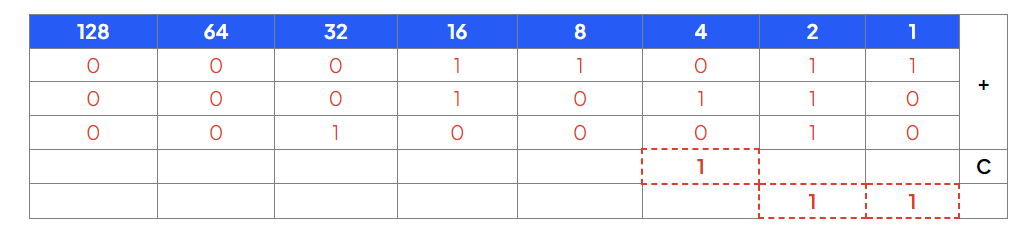
• Repeat until all columns have a value

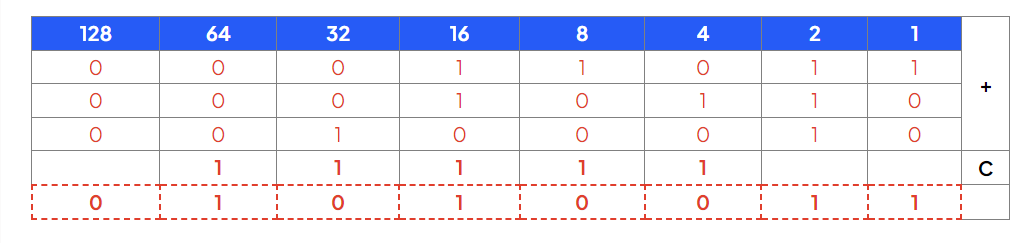
• The sum of adding together binary 00011011 (27), 00010110 (22) and 00100010 (34) is 01010011 (83)

What is an overflow error?

• An overflow error occurs when the result of a binary addition exceeds the available bits

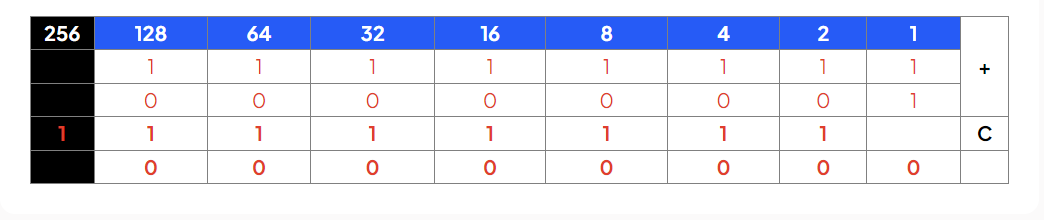
• For example, if you took binary 11111111 (255) and tried to add 00000001 (1) this would cause an overflow error as the result would need a 9th bit to represent the answer (256)