The Effect of Damping (DP IB Physics)

Types of Damping

• In practice, all oscillators eventually stop oscillating

  • Their amplitudes decrease rapidly, or gradually

• This happens due to resistive forces, such as friction or air resistance, which act in the opposite direction to the motion of an oscillator

• Resistive forces acting on an oscillating simple harmonic system cause damping

  • These are known as damped oscillations

• Damping is defined as:

  The reduction in energy and amplitude of oscillations due to resistive forces on the oscillating system

• Damping continues until the oscillator comes to rest at the equilibrium position

• A key feature of simple harmonic motion is that the frequency of damped oscillations does not change as the amplitude decreases

  • For example, a child on a swing can oscillate back and forth once every second, but this time remains the same regardless of the amplitude

Damping on a mass on a spring is caused by a resistive force (F_R) acting in the opposite direction to the motion (blue arrow). This continues until the amplitude of the oscillations reaches zero

Types of Damping

• There are three degrees of damping depending on how quickly the amplitude of the oscillations decreases:

  • Light damping

  • Critical damping

  • Heavy damping

Light Damping

• When oscillations are lightly damped, the amplitude does not decrease linearly

  • It decays exponentially with time

• When a lightly damped oscillator is displaced from the equilibrium, it will oscillate with gradually decreasing amplitude

  • For example, a swinging pendulum decreasing in amplitude until it comes to a stop

A graph for a lightly damped system consists of oscillations decreasing exponentially

• Key features of a displacement-time graph for a lightly damped system:

  • There are many oscillations represented by a sine or cosine curve with gradually decreasing amplitude over time

  • This is shown by the height of the curve decreasing in both the positive and negative displacement values

  • The amplitude decreases exponentially

  • The frequency of the oscillations remains constant, this means the time period of oscillations must stay the same and each peak and trough are equally spaced

Critical Damping

• When a critically damped oscillator is displaced from the equilibrium, it will return to rest at its equilibrium position in the shortest possible time without oscillating

  • For example, car suspension systems prevent the car from oscillating after travelling over a bump in the road

The graph for a critically damped system shows no oscillations and the displacement returns to zero in the quickest possible time

• Key features of a displacement-time graph for a critically damped system:

  • This system does not oscillate, meaning the displacement falls to 0 straight away

  • The graph has a fast decreasing gradient when the oscillator is first displaced until it reaches the x axis

  • When the oscillator reaches the equilibrium position (x = 0), the graph is a horizontal line at x = 0 for the remaining time

Heavy Damping

• When a heavily damped oscillator is displaced from the equilibrium, it will take a long time to return to its equilibrium position without oscillating

• The system returns to equilibrium more slowly than the critical damping case

  • For example, door dampers to prevent them from slamming shut

A heavy damping curve has no oscillations and the displacement returns to zero after a long period of time

• Key features of a displacement-time graph for a heavily damped system:

  • There are no oscillations. This means the displacement does not pass 0

  • The graph has a slow decreasing gradient from when the oscillator is first displaced until it reaches the x-axis

  • The oscillator reaches the equilibrium position (x = 0) after a long period of time, after which the graph remains a horizontal line for the remaining time

Effects of Damping

• The effects of damping can be seen on a resonance curve

• This is a graph of driving frequency f against amplitude A of oscillations

• It has the following key features:

  • When f < f₀, the amplitude of oscillations increases

  • At the peak where f = f₀, the amplitude is at its maximum

    • This is resonance

  • When f > f₀ , the amplitude of oscillations starts to decrease

The maximum amplitude of the oscillations occurs when the driving frequency is equal to the natural frequency of the oscillator

• Damping reduces the amplitude of resonance vibrations

• The height and shape of the resonance curve will therefore change slightly depending on the degree of damping

  • Note: the natural frequency f₀ of the oscillator will remain the same

• As the degree of damping is increased, the resonance graph is altered in the following ways:

  • The amplitude of resonance vibrations decrease, meaning the peak of the curve lowers

  • The resonance peak broadens

  • The resonance peak moves slightly to the left of the natural frequency when heavily damped

• Therefore, damping reduced the sharpness of resonance and reduces the amplitude at resonant frequency

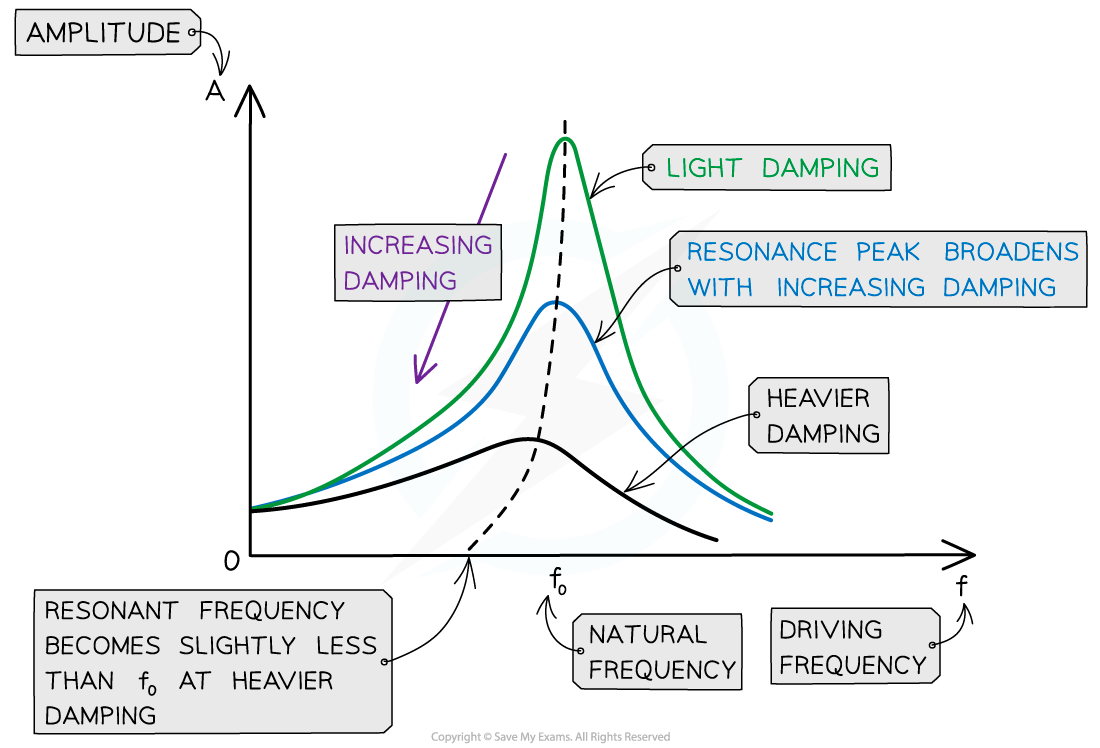
As damping is increased, resonance peak lowers, the curve broadens and moves slightly to the left