Boundary Conditions for Standing Waves (DP IB Physics)

Boundary Conditions

• Stationary waves can form on strings or in pipes

• In both cases, progressive waves travel in a medium (i.e. the string or air) and superimpose with their reflections

• The number of nodes and antinodes that fit within the available length of medium depends on:

  • The frequency of the progressive waves

  • The boundary conditions (i.e. whether the progressive waves travel between two fixed ends, two free ends or a fixed and a free end)

Standing Waves on Stretched Strings

• When guitar strings are plucked, they can vibrate with different frequencies

• The frequency with which a string vibrates depends on:

  • The tension, which is adjusted using rotating 'tuning pegs'

  • The mass per unit length, which is the reason why a guitar has strings of different thicknesses

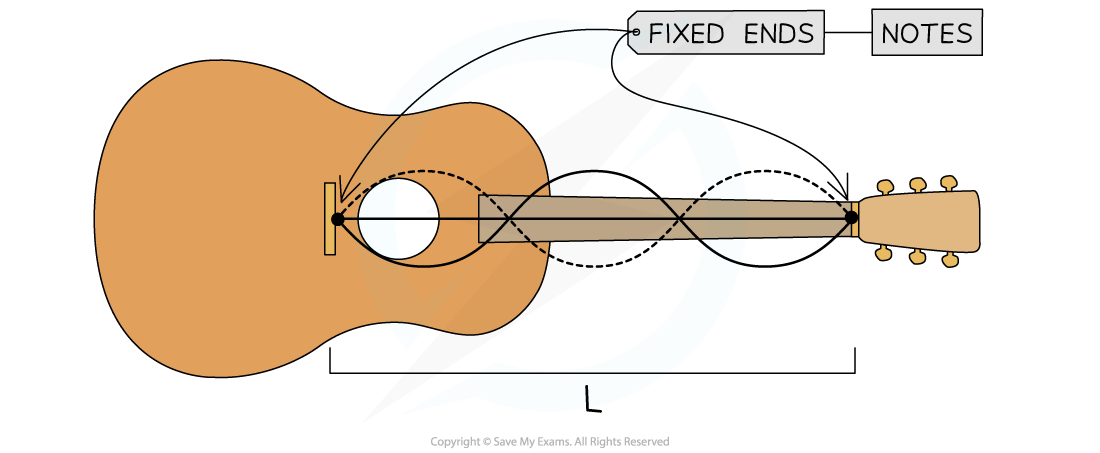
Standing wave on a guitar string

• For a string, the boundary condition can be

  • Fixed at both ends

  • Free at both ends

  • One end fixed, the other free

• At specific frequencies, known as natural frequencies, an integer number of half wavelengths will fit on the length of the string

  • As progressive waves of different natural frequencies are sent along the string, standing waves with different numbers of nodes and antinodes form

Standing Waves in Pipes 

• When the air within a pipe vibrates, longitudinal waves travel along the pipe

• Simply blowing across the open end of a pipe can produce a standing wave in the pipe

• For a pipe, there is more than one possible boundary condition, theses are pipes that are:

  • Closed at both ends

  • Open at both ends

  • Closed at one end and open on the other

Nodes & Antinodes

• When a progressive wave travels towards a free end for a string, or open end for a pipe:

  • The reflected wave is in phase with the incident wave

  • The amplitudes of the incident and reflected waves add up

  • A free end is a location of maximum displacement - i.e. an antinode

Standing wave inside a pipe open at both ends

• When a progressive wave travels towards a fixed end for a string, or closed end for a pipe:

  • The reflected wave is in anti-phase with the incident wave

  • The two waves cancel out

  • A fixed end is a location of zero displacement - i.e. a node

  • The open end is therefore a location of maximum displacement - i.e. an antinode

Standing wave inside a pipe open at both ends