Energy Changes in Simple Harmonic Motion (SHM) (DP IB Physics) : Revision Note
Energy Changes in Simple Harmonic Motion
Simple harmonic motion also involves an interplay between different types of energy: potential and kinetic
The swinging of a pendulum is an interplay between gravitational potential energy and kinetic energy
The horizontal oscillation of a mass on a spring is an interplay between elastic potential energy and kinetic energy
Energy of a Horizontal Mass-Spring System
The system has the maximum amount of elastic potential energy when held so the string is stretched beyond its equilibrium position
When the mass is released, it moves back towards the equilibrium position, accelerating as it goes so the kinetic energy increases
At the equilibrium position, kinetic energy is at its maximum and elastic potential energy is at its minimum
Once past the equilibrium position, the kinetic energy decreases and elastic potential energy increases
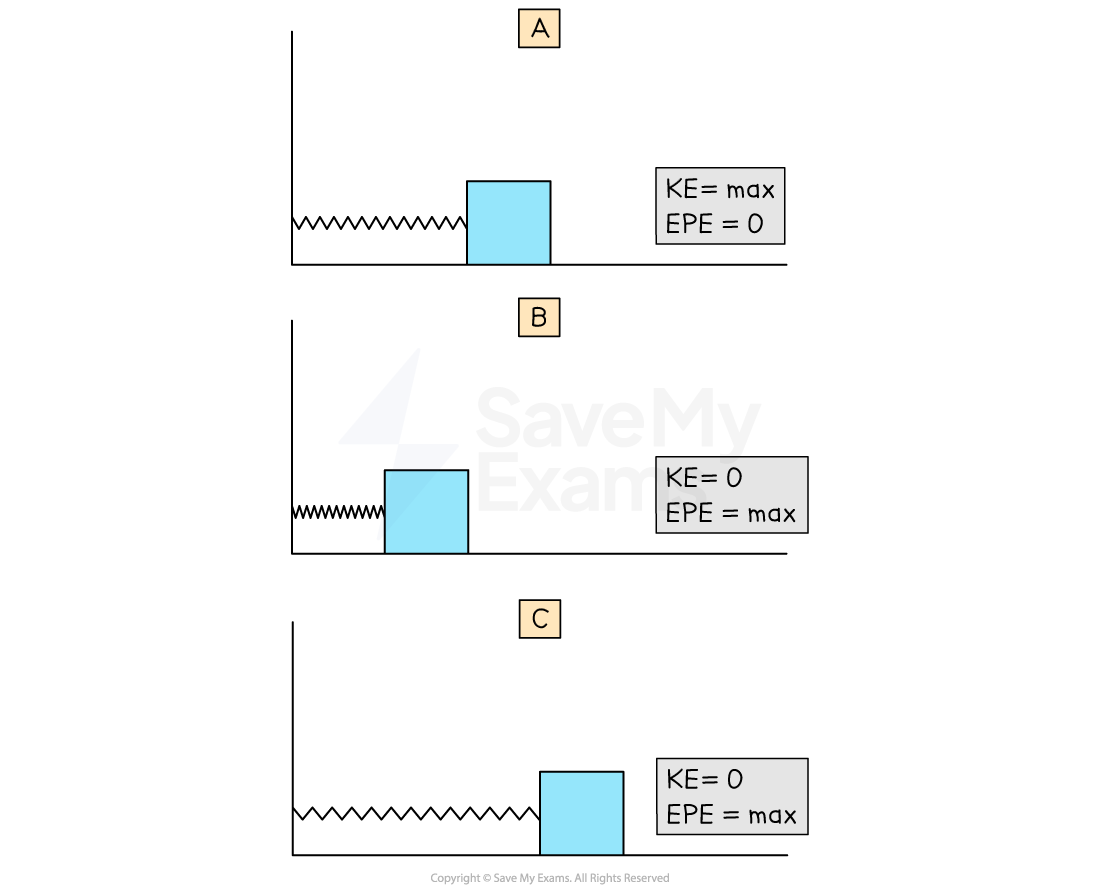
In a horizontal mass-spring system the kinetic energy is maximum in the equilibrium position and the elastic potential energy is maximum in the amplitude position
Energy of a Simple-Pendulum
At the amplitude at the top of the swing, the pendulum has a maximum amount of gravitational potential energy
When the pendulum is released, it moves back towards the equilibrium position, accelerating as it goes so the kinetic energy increases
As the height of the pendulum decreases, the gravitational potential energy also decreases
Once the mass has passed the equilibrium position, kinetic energy decreases and gravitational potential energy increases
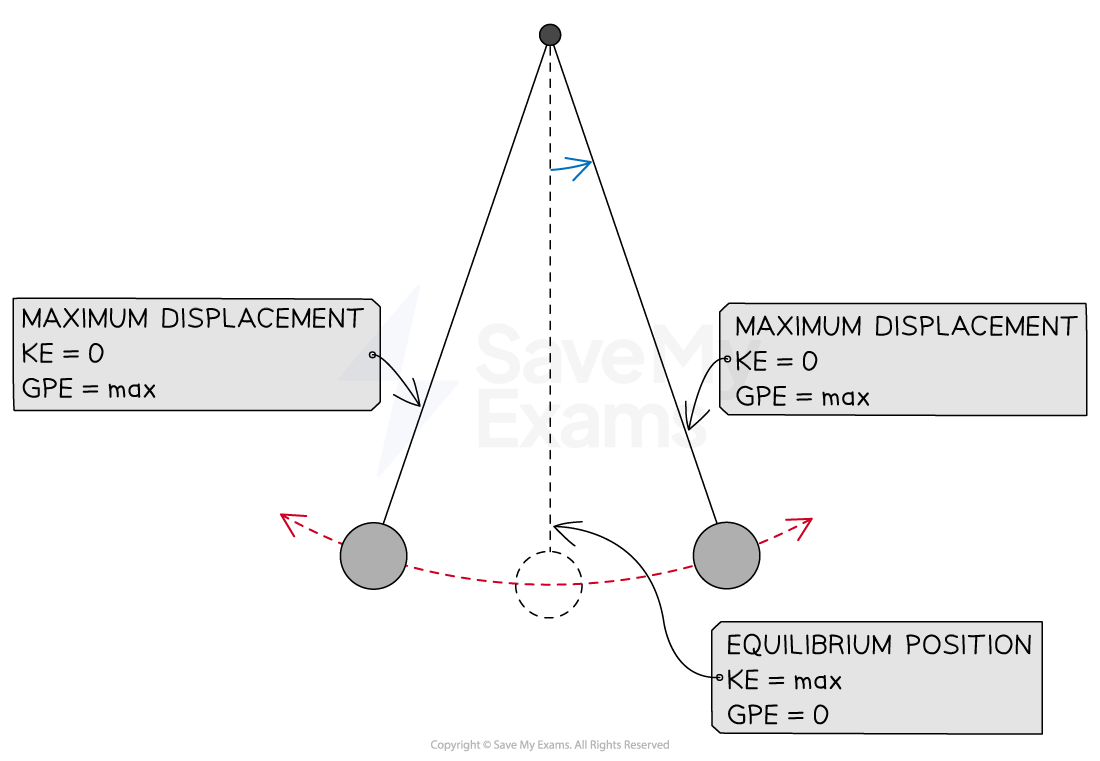
In a simple pendulum system the kinetic energy is maximum in the equilibrium position and the gravitational potential energy is maximum in the amplitude position
Total Energy of an SHM System
The total energy in the system remains constant, but the amount of energy in one form goes up while the amount in the other form goes down
This constant total energy shows how energy in a closed system is never created or destroyed; it is transferred from one store to another
This is the law of conservation of energy
The total energy of a simple harmonic system always remains constant and is equal to the sum of the kinetic and potential energy
The total energy is calculated using the equation:
E = EP + EK
Where:
E = total energy in joules (J)
EP = potential energy in joules (J)
EK = kinetic energy in joules (J)
Remember the equations for potential and kinetic energy:
Gravitational potential energy: Ep = mgh
Elastic potential energy, Ep =
Kinetic energy, Ek =
Energy-Displacement Graph
The kinetic and potential energy transfers go through two complete cycles during one period of oscillation
One complete oscillation reaches the maximum displacement twice (on both the positive and negative sides of the equilibrium position)
You need to be familiar with the graph showing the total, potential and kinetic energy transfers in half an SHM oscillation (half a cycle)
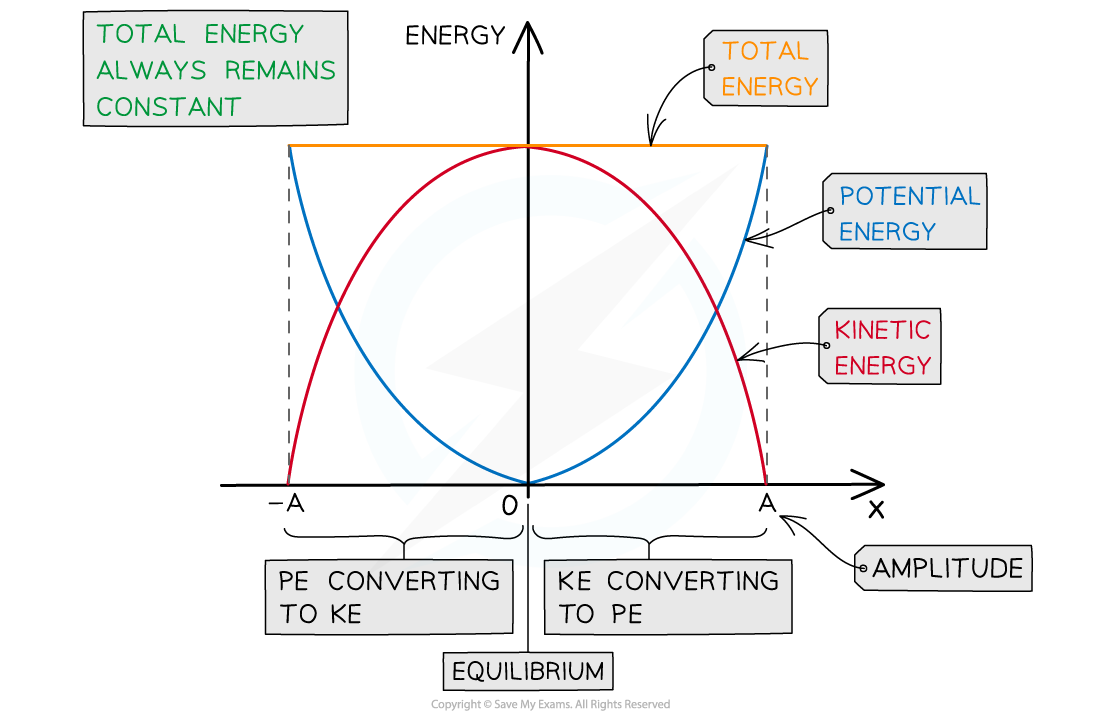
Graph showing the potential and kinetic energy against displacement in half a period of an SHM oscillation
The key features of the energy-displacement graph for half a period of oscillation are:
Displacement is a vector, so, the graph has both positive and negative x values
The potential energy is always maximum at the amplitude positions x = x0, and 0 at the equilibrium position x = 0
This is represented by a ‘U’ shaped curve
The kinetic energy is the opposite: it is 0 at the amplitude positions x = x0, and maximum at the equilibrium position x = 0
This is represented by an ‘n’ shaped curve
The total energy is represented by a horizontal straight line above the curves
Energy-Time Graph for a Simple Pendulum
You also need to be familiar with the graph showing the total, gravitational potential and kinetic energy transfers against time for multiple cycles of a simple pendulum oscillating in simple harmonic motion
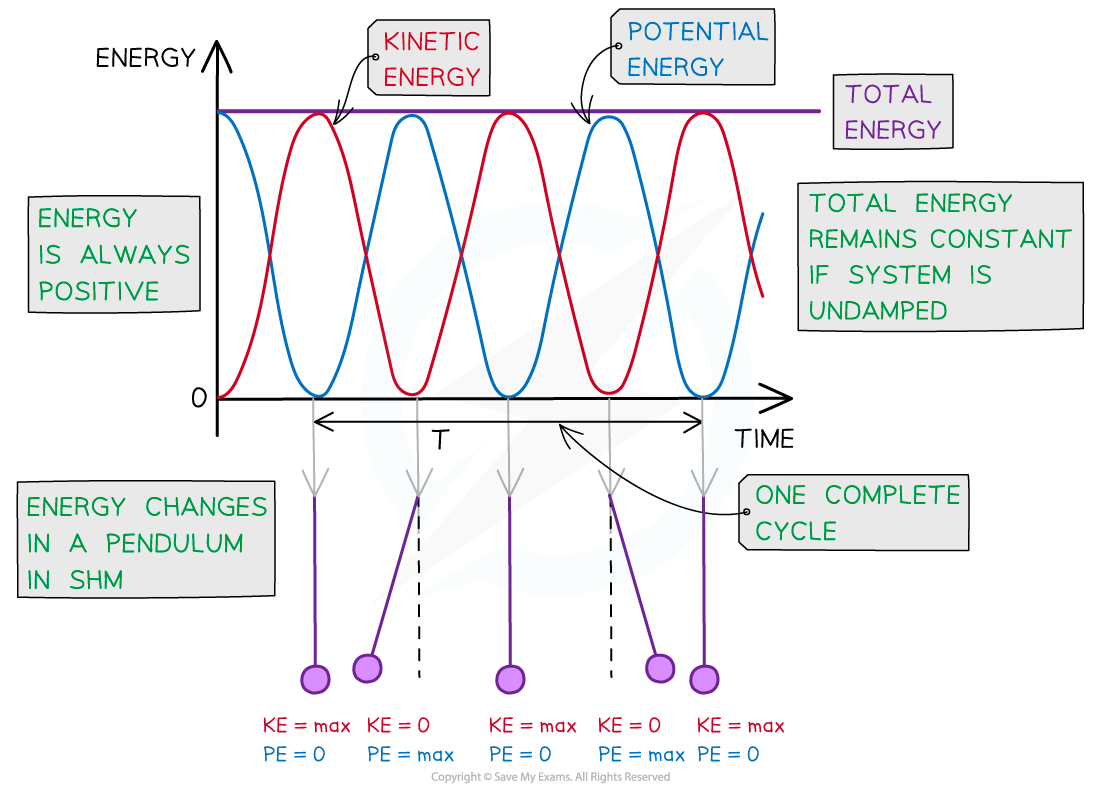
The kinetic and gravitational potential energy of a simple pendulum oscillating in SHM vary periodically
The key features of the simple pendulum energy-time graph are:
Both the kinetic and gravitational potential energy transfers are represented by periodic functions (sine or cosine) which vary in opposite directions to one another
When the gravitational potential energy is 0, the kinetic energy is at its maximum and vice versa
The total energy is represented by a horizontal straight line directly above the energy curves at the maximum kinetic and gravitational potential energy value
Energy is always positive so there are no negative values on the y-axis (Any SHM energy graph drawn with negative energy values is incorrect)
Worked Example
The following graph shows the variation with displacement of the kinetic energy of an object of mass 0.50 kg oscillating with simple harmonic motion. Energy losses can be neglected.

Determine:
(a) The total energy of the object
(b) The amplitude of the oscillations
(c) The maximum velocity of the object
(d) The potential energy of the object when the displacement is x = 1.0 cm
Answer:
(a)
From the graph, the maximum value of kinetic energy is 60 mJ
At the equilibrium position
, the total energy E is exactly equal to the maximum value of kinetic energy
Since energy losses can be neglected, the total energy is constant
Total energy: E = 60 mJ
(b)
The amplitude is equal to the maximum displacement on either side of the equilibrium position (where the kinetic energy is zero)
Amplitude: = 2.0 cm
(c)
The maximum velocity can be found using the maximum kinetic energy in the equation:
Using:
Mass of the object, m = 0.50 kg
Maximum kinetic energy, Ek = 60 mJ = 0.06 J
Maximum velocity: v = 0.49 m s–1
(d)
From the graph, when the displacement is x = 1.0 cm, kinetic energy is EK = 50 mJ
The relationship between total energy E, kinetic energy EK and potential energy EP is:
E = EP + EK
Therefore, the potential energy is
EP = E – EK
EP = 60 – 50 = 10 mJ
Examiner Tips and Tricks
You may be expected to draw as well as interpret energy graphs against time or displacement in exam questions. Make sure the sketches of the curves are as even as possible and use a ruler to draw straight lines, for example, to represent the total energy.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
