Gas Laws (DP IB Physics) : Revision Note
Gas Laws
An ideal gas is one which obeys the relation:
pV ∝ T
Where:
p = pressure of the gas (Pa)
V = volume of the gas (m3)
T = thermodynamic temperature (K)
Turning this into an equation gives:
This is derived from the empirical gas laws for constant pressure, constant temperature and constant volume
Empirical Gas Laws
The ideal gas laws are the experimental relationships between pressure P, volume V and the temperature T of an ideal gas
Boyle’s Law (constant temperature)
Charles’s Law (constant pressure)
Gay-Lussac's Law (constant volume)
The mass and the number of molecules of the gas are assumed to be constant for all experiments
Boyle’s Law
If the temperature T of an ideal gas is constant, then Boyle’s Law is given by:
This means the pressure is inversely proportional to the volume of a gas
The relationship between the pressure and volume for a fixed mass of gas at constant temperature can also be written as:
Where:
P1 = initial pressure (Pa)
P2 = final pressure (Pa)
V1 = initial volume (m3)
V2 = final volume (m3)
The variation of volume and pressure at a constant temperature is shown below:
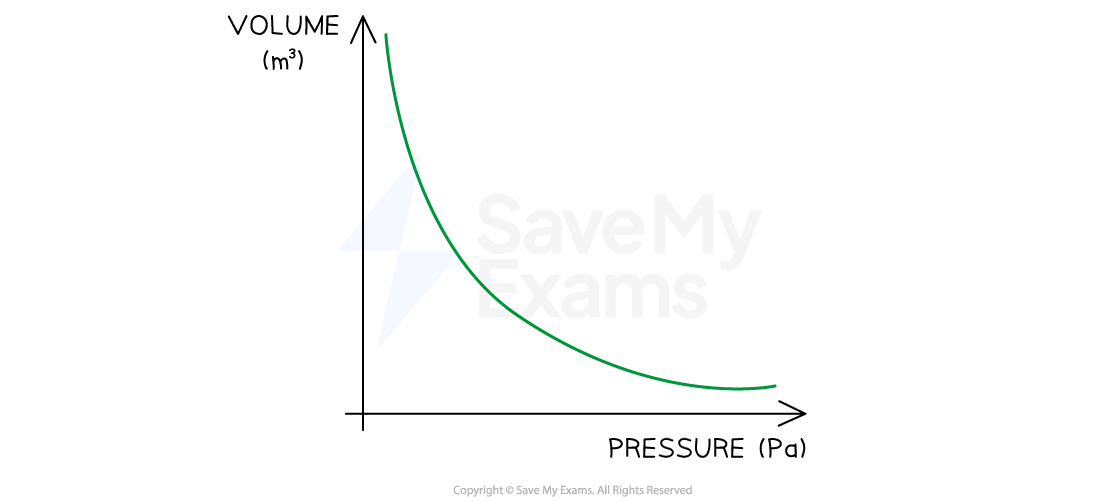
Boyle's Law graph showing pressure is inversely proportional to volume when temperature is constant
If the temperature increases, the graph is further from the origin and vice versa

Boyle's law: gas pressure is inversely proportional to the volume it occupies
Charles's Law
If the pressure P of an ideal gas is constant, then Charles’s law is given by:
This means the volume is proportional to the temperature of a gas
The relationship between the volume and thermodynamic temperature for a fixed mass of gas at constant pressure can also be written as:
Where:
V1 = initial volume (m3)
V2 = final volume (m3)
T1 = initial temperature (K)
T2 = final temperature (K)
The variation of volume and temperature at a constant pressure is shown below:
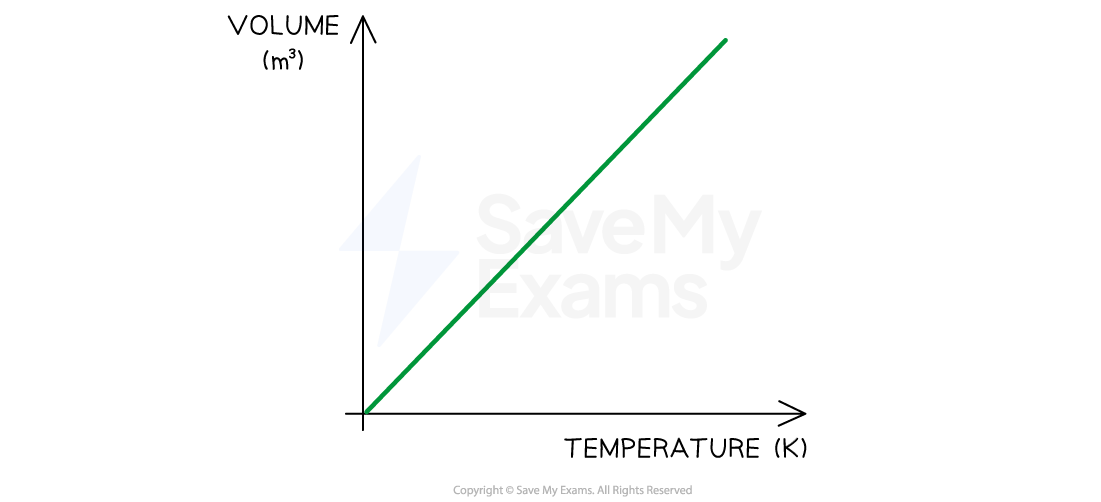
Charles's Law graph showing temperature (in K) is directly proportional to the volume when pressure is constant
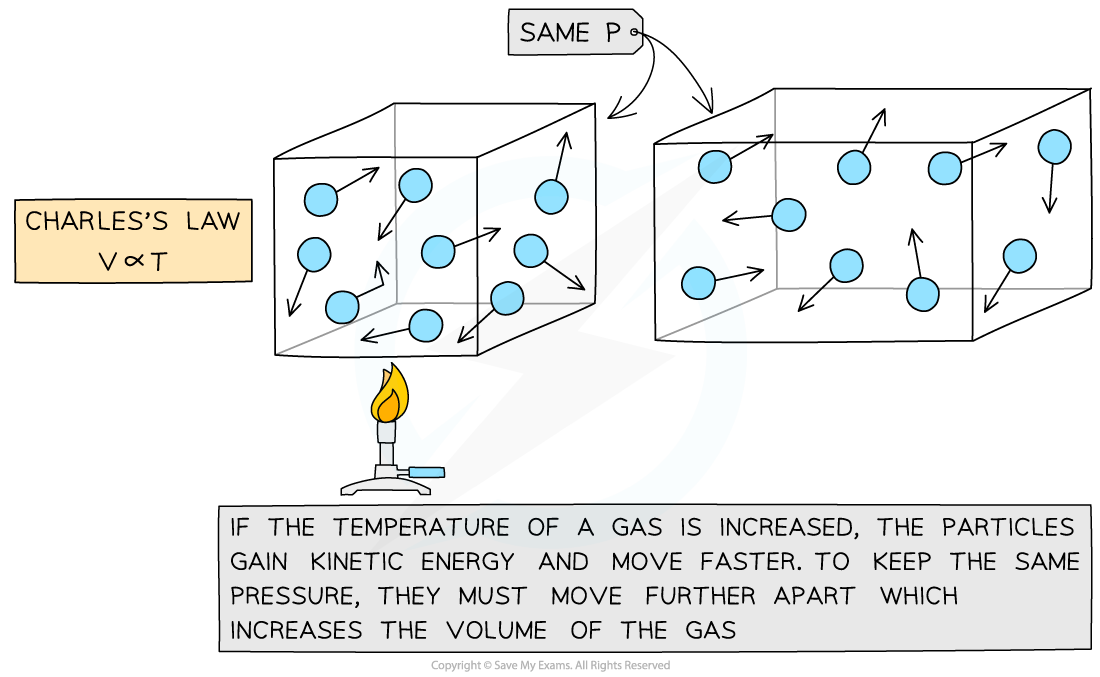
Charles's law: the temperature of a gas is proportional to the volume it occupies
Gay-Lussac's (Pressure) Law
If the volume V of an ideal gas is constant, the Gay-Lussac's or Pressure law is given by:
This means the pressure is proportional to the temperature
The relationship between the pressure and thermodynamic temperature for a fixed mass of gas at constant volume can also be written as:
Where:
P1 = initial pressure (Pa)
P2 = final pressure (Pa)
T1 = initial temperature (K)
T2 = final temperature (K)
The variation of pressure and temperature at a constant volume is shown below:
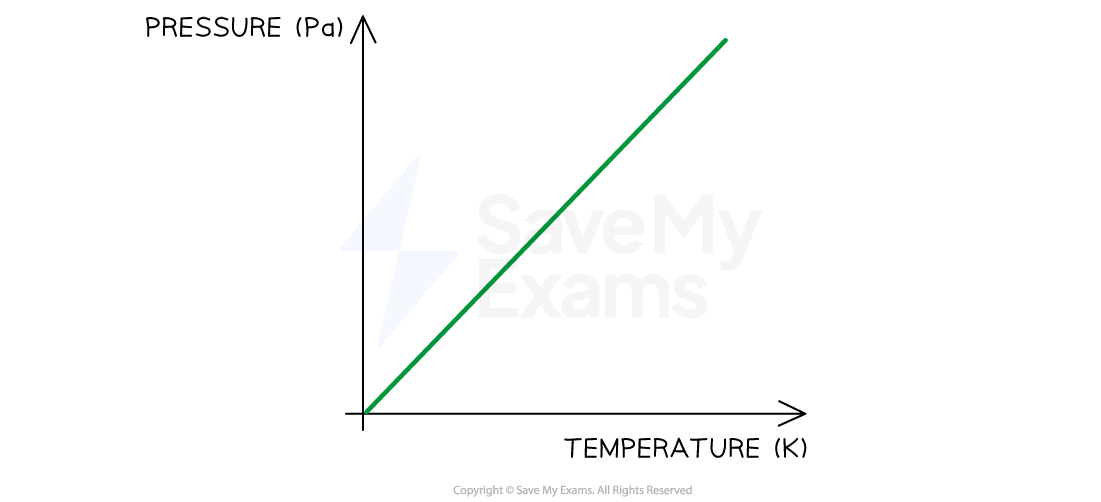
Gay-Lussac's Law graph showing temperature (in K) is directly proportional to pressure when volume is constant
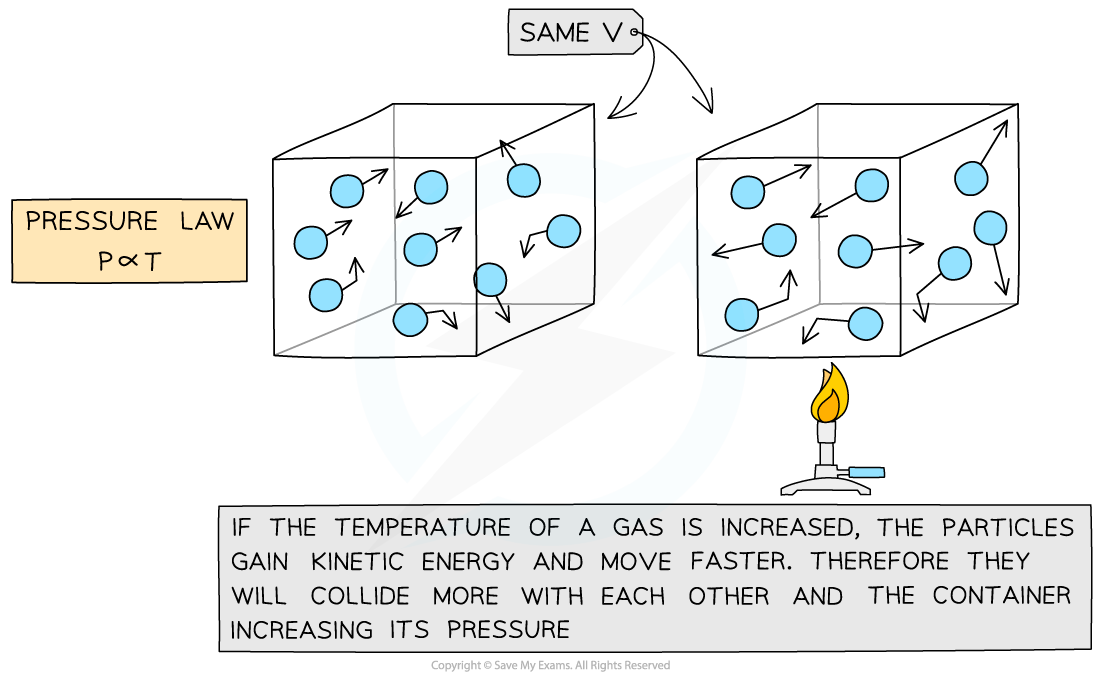
Pressure law: the temperature of a gas is proportional to the gas pressure
Changes in the pressure, temperature or volume of an ideal gas are normally represented on a pressure-volume graph
These are covered in more detail in the thermodynamics topic
Worked Example
An ideal gas is in a container of volume 4.5 × 10-3 m3.The gas is at a temperature of 30 °C and a pressure of 6.2 × 105 Pa.
Calculate the pressure of the ideal gas in the same container when it is heated to 40 °C.
Answer:
Step 1: List the known quantities
Volume, V = 4.5 × 10-3 m3
Inital temperature, T1 = 30 °C
Pressure, P = 6.2 × 105 Pa
Final temperature, T2 = 40 °C
Step 2: State the ideal gas equation
pV ∝ T
pV = kT
Where k = the constant of proportionality
Step 3: Rearrange for the constant of proportionality

Step 4: Convert temperature T into Kelvin
θ °C + 273.15 = T K
30 °C + 273.15 = 303.15 K
Step 5: Substitute in known value into the constant of the proportionality equation
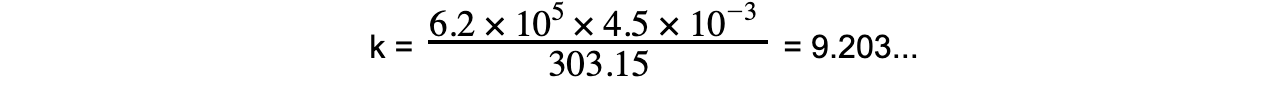
Step 6: Rearrange the ideal gas relation equation for pressure
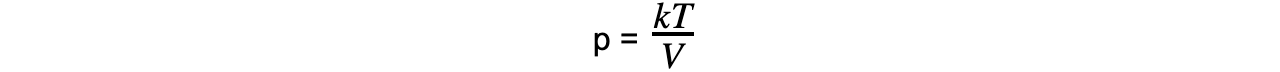
Step 7: Substitute in new values
k = 9.203
T = 40 °C = 40 + 273.15 = 313.15 K
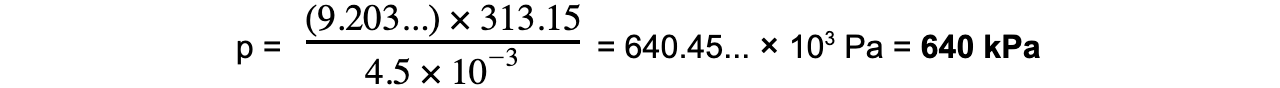
Examiner Tips and Tricks
Make sure to convert the temperature into kelvin before substituting into any gas law equation.
To know which gas laws to use, look at what values you've already been provided in the question. If it helps, label these as V1, T1 etc. or look out for what quantity has been kept constant.
In the worked example, make sure not to get mixed up with this constant k with the Boltzmann constant kB. The constant depends on which ideal gas equation you use. It will be either nR or kBT.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
