Revision NotesExam QuestionsFlashcardsPast Papers
IBPhysicsDPSLRevision NotesSpace, Time & MotionWork, Energy & PowerWork Done

Work Done (DP IB Physics)

Revision Note

Ashika

Author

Ashika

Last updated

DP Physics: SLDP Physics: HL

Work Done

  • The work done by a force is equivalent to a transfer of energy

    • The units of work done are newton metres

    • 1 N m = 1 J

  • The work done by a resultant force on a system is equal to the change in energy in that system

  • Mechanical work is defined as

    The transfer of energy when an external force causes an object to move over a certain distance

  • If a constant force is applied in the line of an object's displacement (i.e. parallel to it), the work done can be calculated using the equation:

W space equals space F s

  • Where:

    • W = work done (J)

    • F = constant force applied (N)

    • s = displacement (m)

  • In the diagram below, the man’s pushing force on the block is doing work as it is transferring energy to the block

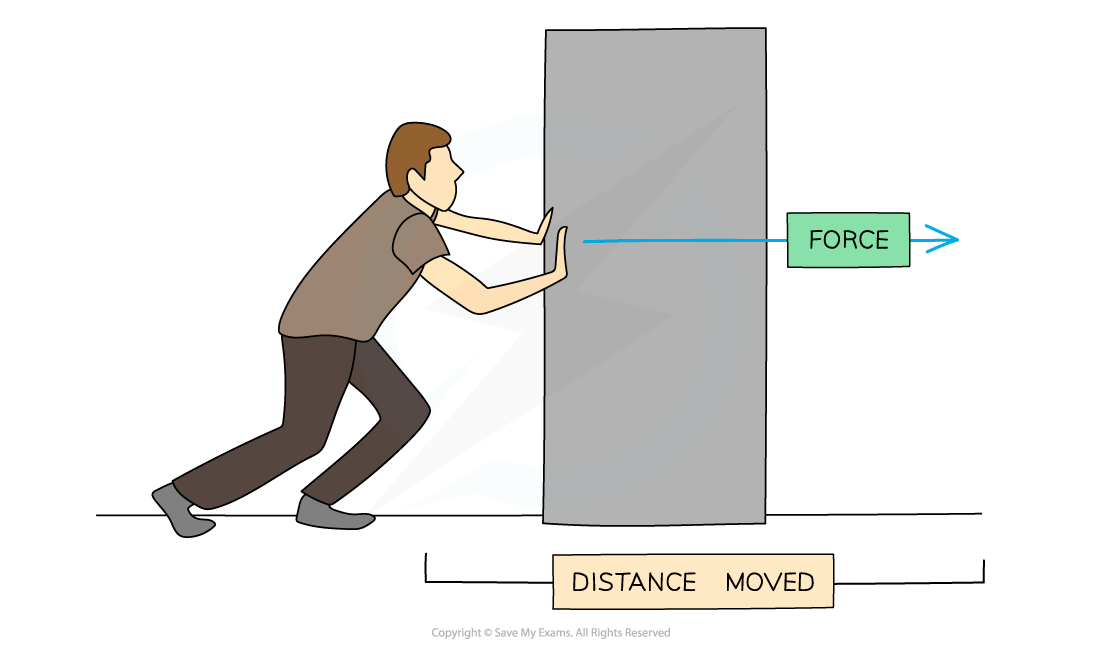
    Work done diagram, downloadable AS & A Level Physics revision notes

Work is done when a force is used to move an object over a distance

  • When pushing a block, work is done against friction and energy is transferred from the man to the block

  • The kinetic energy is transferred to other forms of energy such as heat and sound

  • When plotting a graph of average force applied against displacement, the area under the graph is equal to the work done

  • Sometimes the direction of motion of an object is not parallel to the direction of the force

  • If the force is at an angle θ to the object's displacement, the work done is calculated by:

W space equals space F s cos theta 

  • Where θ is the angle, in degrees, between the direction of the force and the motion of the object

    • When θ is 0 (the force is in the direction of motion) then cos theta space equals space 1 and W space equals space F s

  • For horizontal motion, cos θ is used

  • For vertical motion,  sin θ is used

    • Always consider the horizontal and vertical components of the force

    • The component needed is the one that is parallel to the displacement

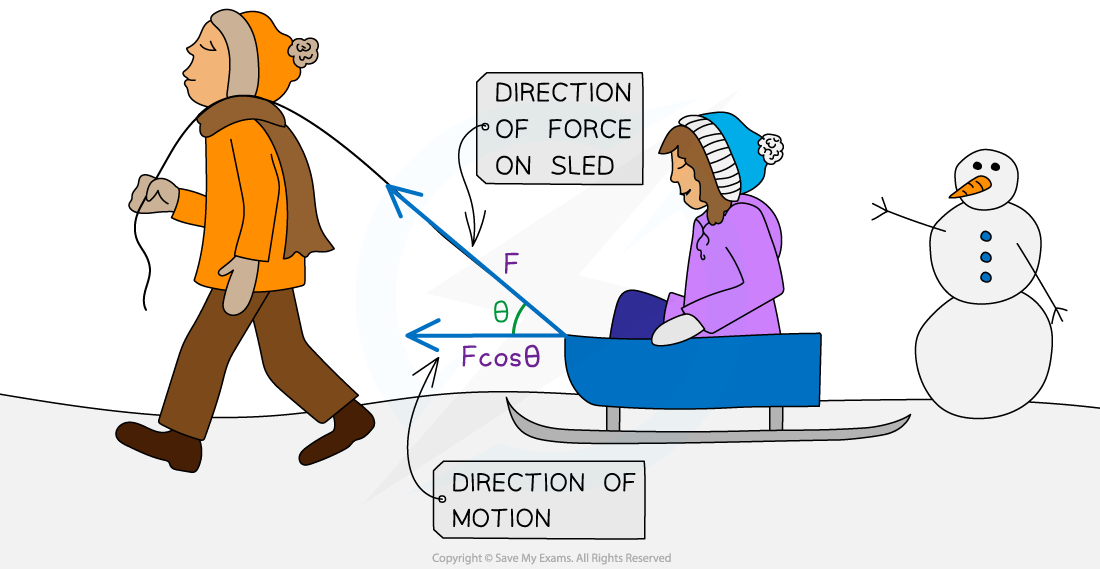
Work Done at an Angle, downloadable AS & A Level Physics revision notes

When the force is at an angle, only the component of the force in the direction of motion is considered for the work done

Worked Example

The diagram shows a barrel of weight 2.5 × 103 N on a frictionless slope inclined at 40° to the horizontal.

WE - Work done on barrel question image, downloadable AS & A Level Physics revision notes

A force is applied to the barrel to move it up the slope at a constant speed. The force is parallel to the slope.

What is the work done in moving the barrel a distance of 6.0 m up the slope?

A. 7.2 × 103 J               

B. 2.5 × 104 J             

C. 1.1 × 104 J               

D. 9.6 × 103 J

WE - Work done on barrel answer image, downloadable AS & A Level Physics revision notes

Worked Example

An 80 kg person pulls a 15 kg box along using a rope which is at 40° from the horizontal as shown below. The person is pulling with a force of 40 N and moves the box 20 m horizontally from its starting position against a constant friction force of 5.0 N.

Calculate the work that has been done on the box in the direction of its motion.

Work-done-Worked-Example, downloadable IB Physics revision notes

Answer

Step 1: List the known quantities

  • The angle between the rope and the horizontal, θ = 40°

  • The pulling force (along rope) = 40 N

  • Horizontal distance moved by box, s = 20 m

  • Frictional force = 5.0 N

Step 2: Resolve the pulling force in the rope into its horizontal component

2-3-4-work-done-we-step-2_sl-physics-rn

  • The horizontal component of the pulling force is the only part of the pulling force aligned with the direction of work

  • Hence, that is the component that is needed to continue solving this problem

  • The horizontal component can be resolved from:

cos open parentheses 40 close parentheses space cross times space 40 space equals space 30.6 space straight N to the right

Step 3: Find the resultant force for the motion

  • The resultant force can be found from the interaction between the horizontal component of the pulling force and the friction force:

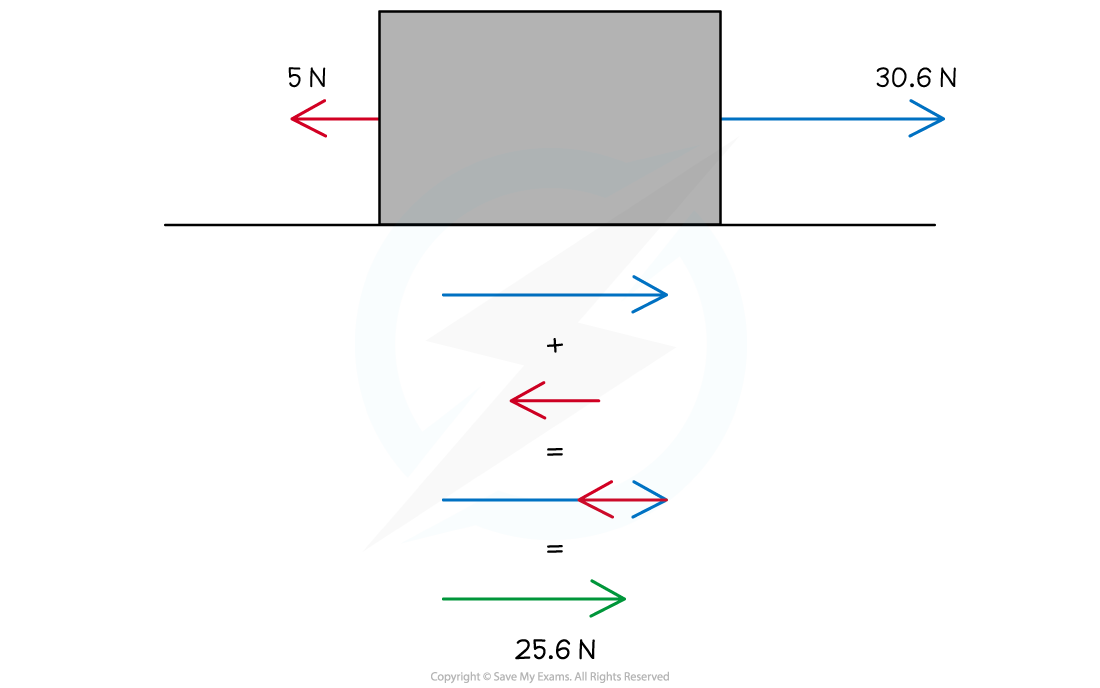
2-3-4-work-done-we-step-3_sl-physics-rn

30.6 space plus space open parentheses negative 5 close parentheses space equals space 25.6 space straight N to the right

Step 4: Calculate the work done

  • Use the equation for work done given the resultant force and distance moved in the horizontal plane

W space equals space F s cos theta

  • The cos θ has already been accounted for so that the resultant force could be found when combined with friction

  • Therefore:

W space equals space F s space equals space 25.6 space cross times space 20 space equals space 512 space straight J

W = 512 J

Examiner Tips and Tricks

Sometimes exam questions will include more values than you need to use in the solution - this is purposefully done to confuse you. For example, in the second worked example above, the question supplies the mass of the person and the box, however, these quantities are not needed for the calculation.

Always consider the horizontal and vertical components of the force. The component needed is the one that is parallel to the displacement. The equation with cos theta is given on your data sheet, but you only need to use this if the force is applied at an angle to the displacement.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Sankey DiagramsNext:Kinetic Energy
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.