Isotopes & Radioactive Decay (DP IB Physics)

Isotopes

• Elements are defined by a fixed number of protons in their atoms

  • For example, all hydrogen atoms have 1 proton, and all carbon atoms have 6 protons

• However, atoms of an element can have different numbers of neutrons

  • These different versions of elements are called isotopes

• An isotope is defined as:

  Nuclei that have the same number of protons but different numbers of neutrons

• For example, hydrogen has two isotopes, deuterium and tritium

  • All three isotopes contain 1 proton, but different numbers of neutrons

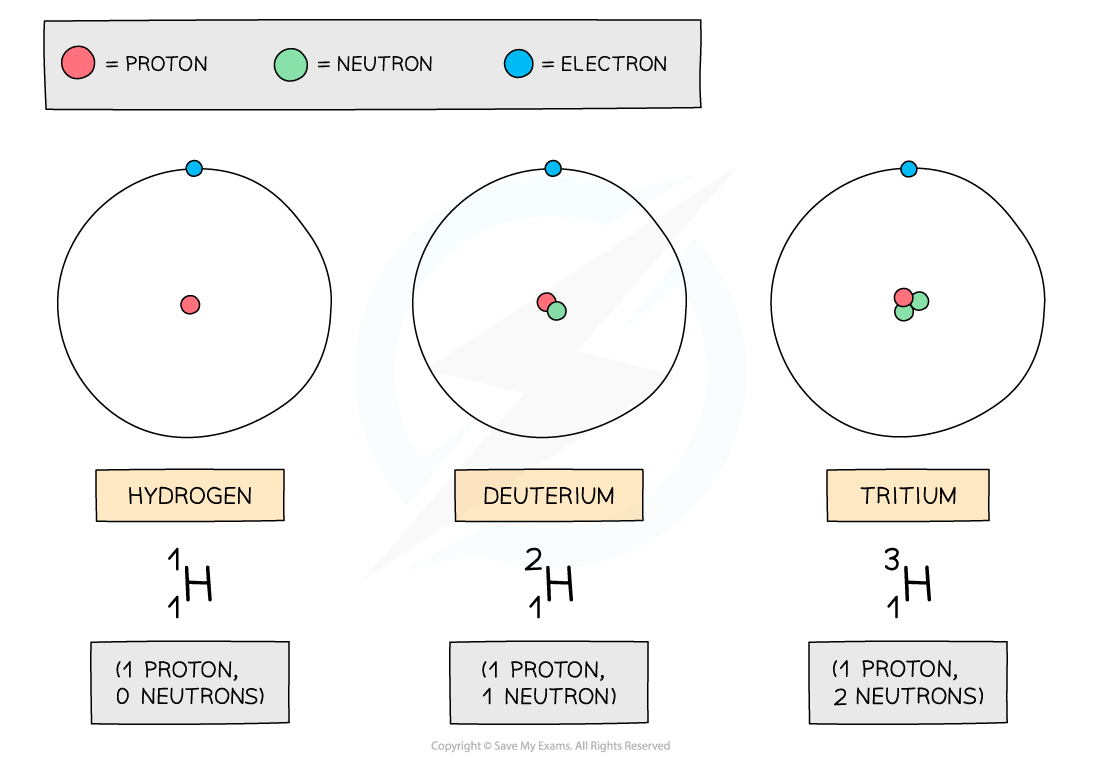
The three atoms shown above are all forms of hydrogen, but they each have different numbers of neutrons

• Since nucleon number A includes the number of protons and neutrons, an isotope of an element will have

  • A fixed proton number, Z

  • A different nucleon number, A

• Some isotopes have an imbalance of neutrons and protons which makes them unstable

  • This means they constantly decay and emit radiation to achieve a more stable form

  • This can happen from anywhere between a few nanoseconds to 100,000 years

Isotopic Data

• Isotopic data is defined as:

  The relative amounts of different isotopes of an element present within a substance

• The mass of an element is displayed on the periodic table as relative atomic mass

• This takes the masses and abundances of all the naturally occurring isotopes of an element into account 

Isotopic data is used to determine the relative atomic masses of elements on the periodic table

• The relative atomic mass of an element can be calculated using the relative abundance values

• The percentage abundance of different isotopes in a sample can be obtained using a mass spectrometer

Table of isotopic data for a sample of oxygen

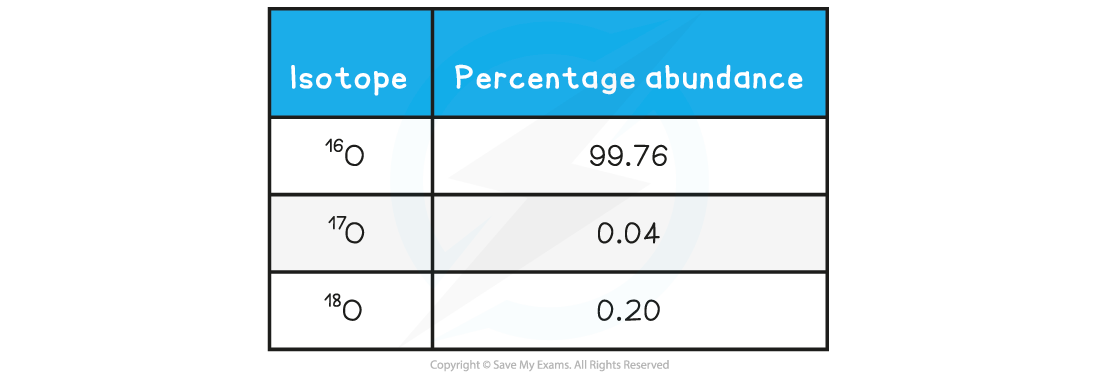
• For example, a sample of oxygen may contain three isotopes: ,  and 

• The relative atomic mass of this sample of oxygen can be calculated using:

(16 × 0.9976) + (17 × 0.0004) + (18 × 0.002) = 16.0044

• To two decimal places, the relative atomic mass of the sample of oxygen is 16.00

• A common use of isotopic data is carbon dating of archaeological artefacts 

  • This involves using the ratio of the amount of stable isotope carbon-12, to the amount of unstable isotope, carbon-14

  • The age of a sample of dead tissue can be determined by comparing the ratio of these isotopes to the ratio in a sample of living tissue

Radioactive Decay

• Radioactive decay is defined as:

  The spontaneous disintegration of a nucleus to form a more stable nucleus, resulting in the emission of an alpha, beta or gamma particle

• The random nature of radioactive decay can be demonstrated by observing the count rate of a Geiger-Muller (GM) tube

  • When a GM tube is placed near a radioactive source, the counts are found to be irregular and cannot be predicted

  • Each count represents a decay of an unstable nucleus

• These fluctuations in count rate on the GM tube provide evidence for the randomness of radioactive decay

The variation of count rate over time of a sample radioactive gas. The fluctuations show the randomness of radioactive decay

Characteristics of Radioactive Decay

• Radioactive decay is both spontaneous and random

• A spontaneous process is defined as:

  A process which cannot be influenced by environmental factors

• This means radioactive decay cannot be affected by environmental factors such as:

  • Temperature

  • Pressure

  • Chemical conditions

• A random process is defined as:

  A process in which the exact time of decay of a nucleus cannot be predicted

• Instead, the nucleus has a constant probability, ie. the same chance, of decaying in a given time

• Therefore, with large numbers of nuclei, it is possible to statistically predict the behavior of the entire group