Revision NotesExam QuestionsFlashcardsPast Papers
IBPhysicsDPSLRevision NotesFieldsMotion in Electromagnetic FieldsMagnetic Force on a Charge

Magnetic Force on a Charge (DP IB Physics)

Revision Note

Ann Howell

Last updated

DP Physics: SLDP Physics: HL

Magnetic Force on a Moving Charge

  • A moving charge produces its own magnetic field

    • When interacting with an applied magnetic field, it will experience a force

  • The force F on an isolated particle with charge Q moving with speed v at an angle θ to a magnetic field with flux density B is defined by the equation

F space equals space B q v space sin space theta

  • Where:

    • F = magnetic force on the particle (N)

    • B = magnetic flux density (T)

    • q = charge of the particle (C)

    • v = speed of the particle (m s−1)

  • Current is taken as the rate of flow of positive charge (i.e. conventional current)

    • This means that the direction of the current for a flow of negative charge (e.g. a beam of electrons) is in the opposite direction to its motion

  • As with a current-carrying conductor, the maximum force on a charged particle occurs when it travels perpendicular to the field

    • This is when θ = 90°, so sin θ = 1

  • The equation for the magnetic force becomes:

F space equals space B q v

  • F, B and v are mutually perpendicular, therefore:

    • If the direction of the particle's motion changes, the magnitude of the force will also change

    • If the particle travels parallel to a magnetic field, it will experience no magnetic force

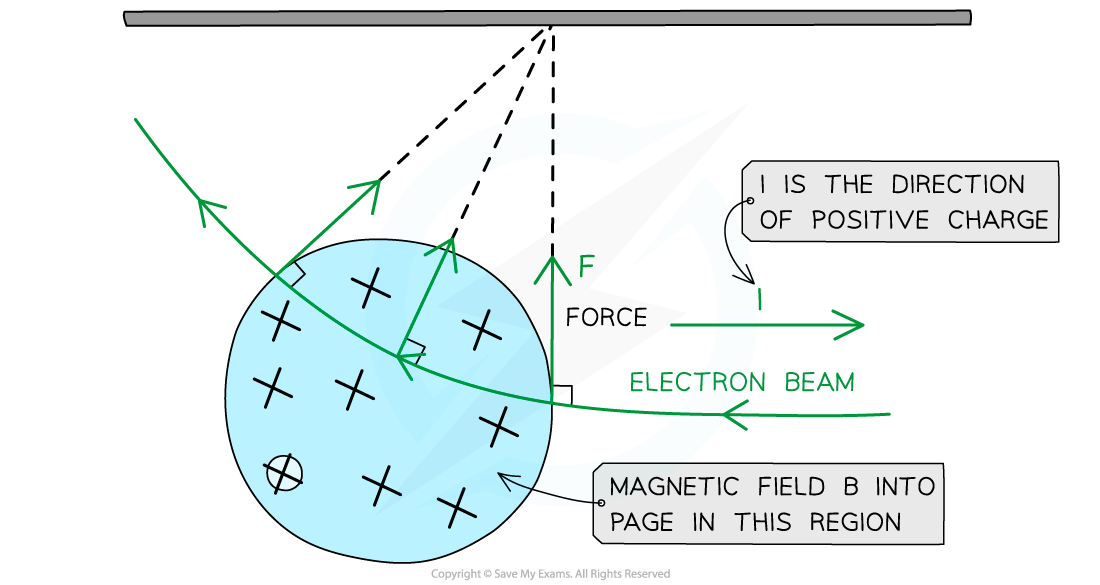
Force on isolated moving charge, downloadable AS & A Level Physics revision notes

The force on an isolated moving charge is perpendicular to its motion and the magnetic field B

  • From the diagram above, when a beam of electrons enters a magnetic field which is directed into the page: 

    • Electrons are negatively charged, so current I is directed to the right (as motion v is directed to the left)

    • Using Fleming’s left hand rule, the force on an electron will be directed upwards

Worked Example

An electron moves in a uniform magnetic field of flux density 0.2 T at a velocity of 5.3 × 107 m s−1.

(a) Calculate the force on the electron when it moves perpendicular to the field.

(b) Determine the angle the electron must make with the field for the force in (a) to half.

Answer:

(a)

Step 1: Write out the known quantities

  • Velocity of the electron, v = 5.3 × 107 m s−1

  • Charge of an electron, q = 1.60 × 10−19 C

  • Magnetic flux density, B = 0.2 T

Step 2: Write down the equation for the magnetic force on an isolated particle

F space equals space B q v space sin space theta

  • The electron moves perpendicular (θ = 90°) to the field, so sin θ = 1

F space equals space B q v

Step 3: Substitute in values, and calculate the force on the electron

F = (0.2) × (1.60 × 10−19) × (5.3 × 107) = 1.7 × 10−12 N (2 s.f.)

(b)

Step 1: Write an expression for the ratio of the two forces

  • When the electron moves perpendicular to the field: F subscript perpendicular space equals space B q v

  • When the electron moves at angle θ to the field: F subscript theta space equals space B q v space sin space theta

  • The ratio of these forces is

F subscript theta over F subscript perpendicular space equals space fraction numerator B q v space sin space theta over denominator B q v end fraction space equals space sin space theta

Step 2: Determine the angle when the ratio of the forces is equal to one-half

  • When the force halves, the ratio is

F subscript theta over F subscript perpendicular space equals space 1 half

  • The angle this occurs at is

sin space theta space equals space 1 half

theta space equals space sin to the power of negative 1 end exponent space open parentheses 1 half close parentheses space equals space 30 degree

Examiner Tips and Tricks

Remember not to mix this up with F = BIL!

  • F = BIL is for a current-carrying conductor

  • F = Bqv is for an isolated moving charge (which may be inside a conductor)

Direction of Force on a Moving Charge

  • The direction of the magnetic force on a charged particle depends on

    • The direction of flow of current

    • The direction of the magnetic field

  • This can be found using Fleming's left-hand rule

  • The second finger represents the current flow or the flow of positive charge

    • For a positive charge, the current points in the same direction as its velocity 

    • For a negative charge, the current points in the opposite direction to its velocity

flemings-left-hand-rule-charged-particles

Fleming’s left-hand rule allows us to determine the direction of the force on a charged particle

  • From the diagram above, when a positive charge enters a magnetic field from left to right, using Fleming's left-hand rule:

    • The first finger (field) points into the page

    • The second finger (current) points to the right

    • The thumb (force) points upwards

  • When a charged particle moves in a uniform magnetic field, the force acts perpendicular to the field and the particle's velocity

    • As a result, it follows a circular path 

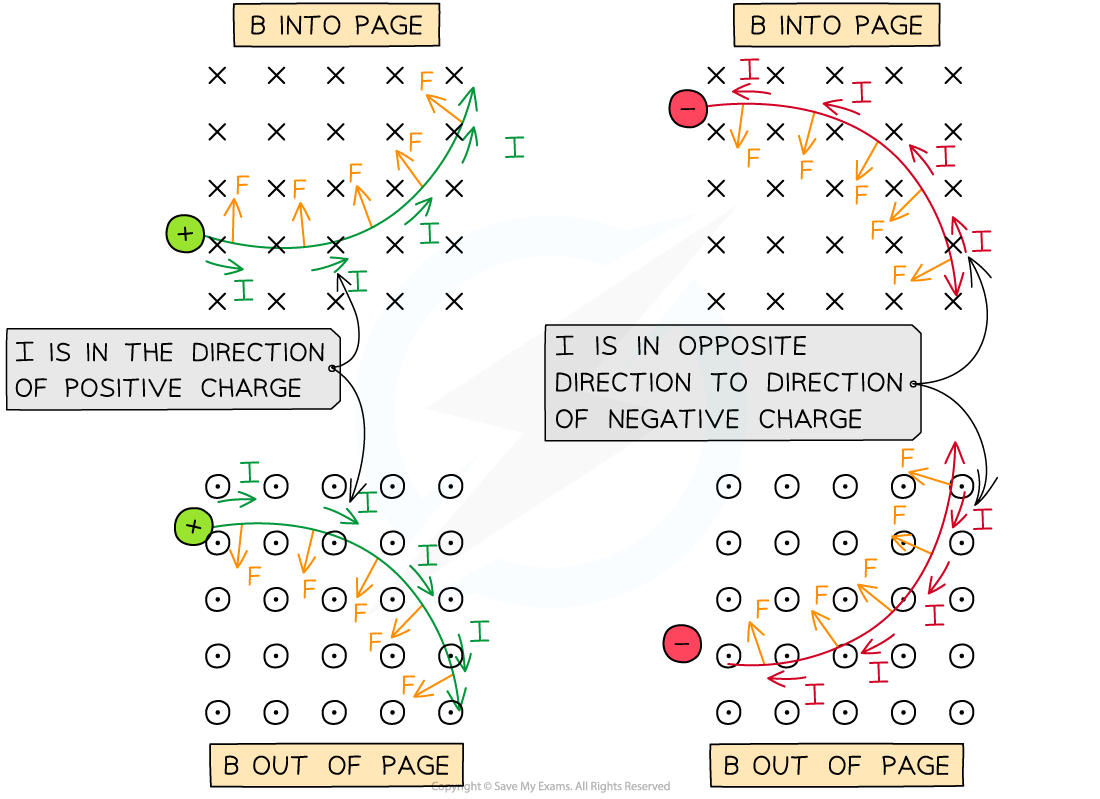
Direction of Magnetic Force, downloadable AS & A Level Physics revision notes

The direction of the magnetic force F on positive and negative particles in a B field in and out of the page

Examiner Tips and Tricks

Remember not to get this mixed up with Fleming's right-hand rule. That is used for a generator (or dynamo), where a current is induced in the conductor. Fleming's left-hand rule is sometimes referred to as the 'Fleming's left-hand rule for motors'.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Magnetic Force between Two Parallel ConductorsNext:Charged Particles in Magnetic Fields
    Ann Howell

    Author: Ann Howell

    Expertise: Physics Content Creator

    Ann obtained her Maths and Physics degree from the University of Bath before completing her PGCE in Science and Maths teaching. She spent ten years teaching Maths and Physics to wonderful students from all around the world whilst living in China, Ethiopia and Nepal. Now based in beautiful Devon she is thrilled to be creating awesome Physics resources to make Physics more accessible and understandable for all students, no matter their schooling or background.