Revision NotesExam QuestionsFlashcardsPast Papers
IBPhysicsDPSLRevision NotesFieldsMotion in Electromagnetic FieldsCharged Particles in Electric & Magnetic Fields

Charged Particles in Electric & Magnetic Fields (DP IB Physics)

Revision Note

Ann Howell

Last updated

DP Physics: SLDP Physics: HL

Charged Particles in Electric & Magnetic Fields

  • A charged particle moving in perpendicularly orientated uniform electric and magnetic fields will experience

    • a force parallel to the electric field

    • a force perpendicular to the magnetic field

  • One particular orientation is:

    • a charged particle moving with speed v to the right of the x-axis

    • an electric field E directed up the y-axis

    • a magnetic field B directed out of the page on the z-axis

  • Hence, the three vectors are perpendicular to each other

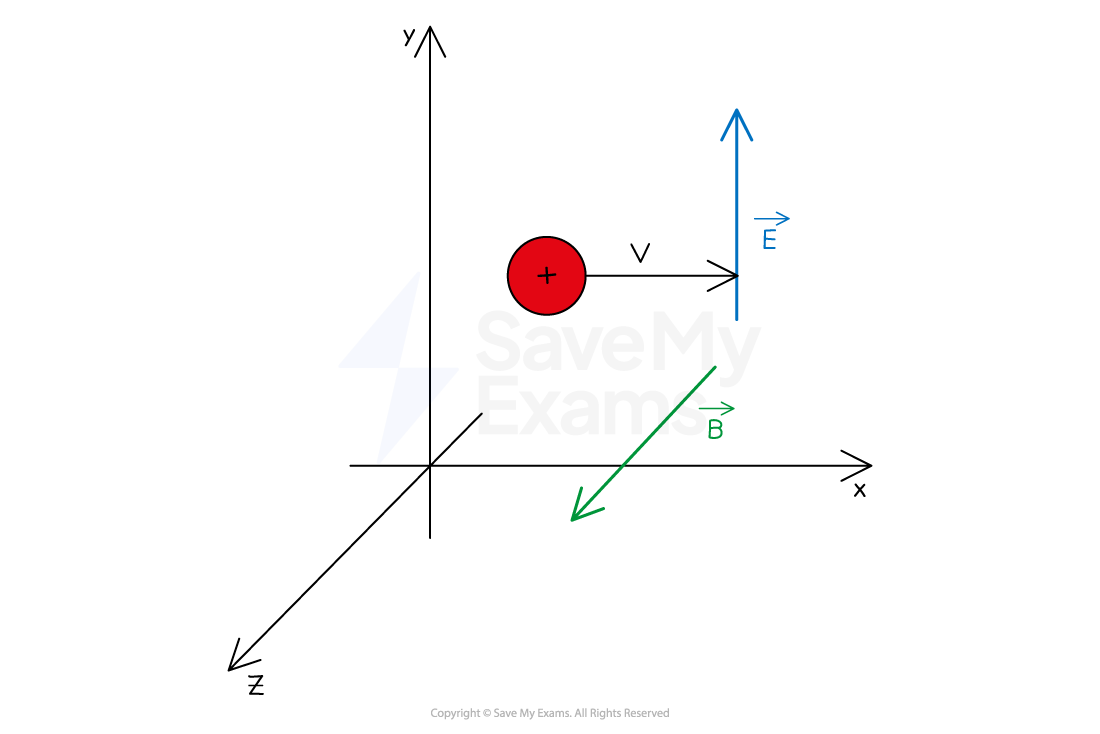
4-2-perpendicular-electric-and-magnetic-fields

An example of the orientation of an electric field perpendicular to a magnetic field

Motion of a Positively Charged Particle

  • When the particle is positively charged

    • the electric force acts upwards, in the same direction as the electric field

    • the magnetic force acts downwards, perpendicular to the magnetic field

  • Using Fleming's left hand rule:

    • Field (first finger): the magnetic field is directed out of the page

    • Current (second finger): the positive charge moves to the right

    • Force (thumb): the magnetic force acts downwards

  • Hence, the electric force and magnetic force act in opposite directions on the positive charge

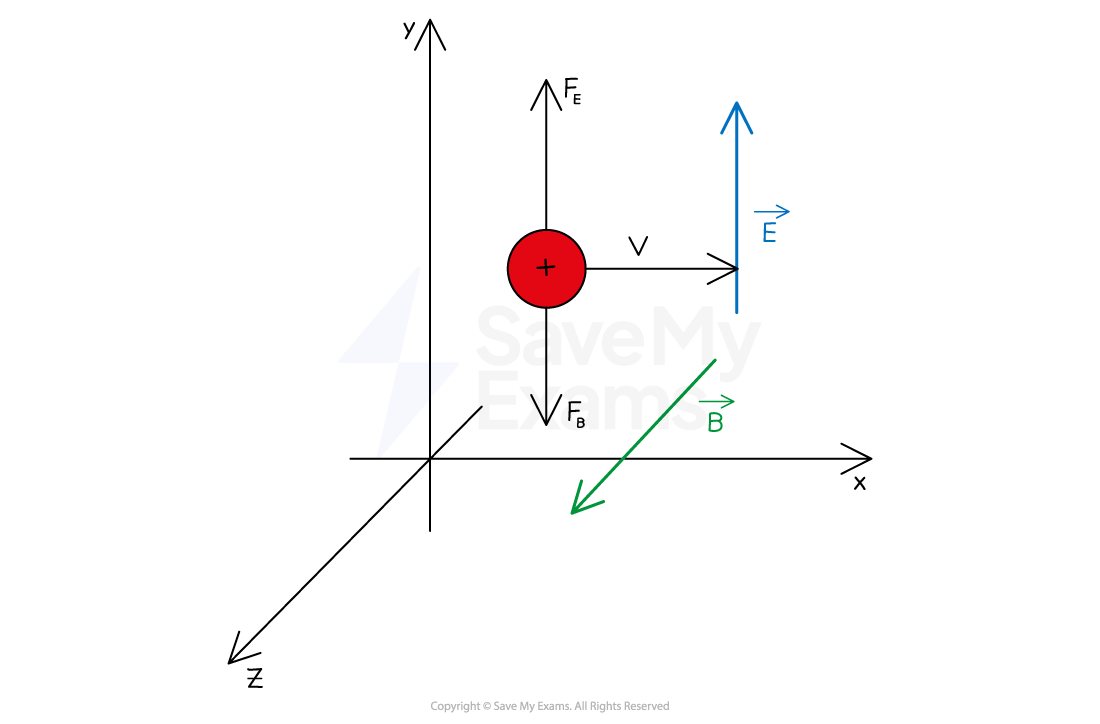
4-2-perpendicular-electric-and-magnetic-fields-with-forces

The electric force acts up the page and the magnetic force acts in the opposite direction down the page

 

Motion of a Negatively Charged Particle

  • When the particle is negatively charged

    • the electric force acts downwards, in the opposite direction to the electric field

    • the magnetic force acts upwards, perpendicular to the magnetic field

  • Using Fleming's left hand rule:

    • Field (first finger): the magnetic field is directed out of the page

    • Current (second finger): the positive charge moves to the left (since the negative charge moves to the right, in the opposite direction)

    • Force (thumb): the magnetic force acts upwards

  • Hence, the electric force and magnetic force act in opposite directions on the negative charge

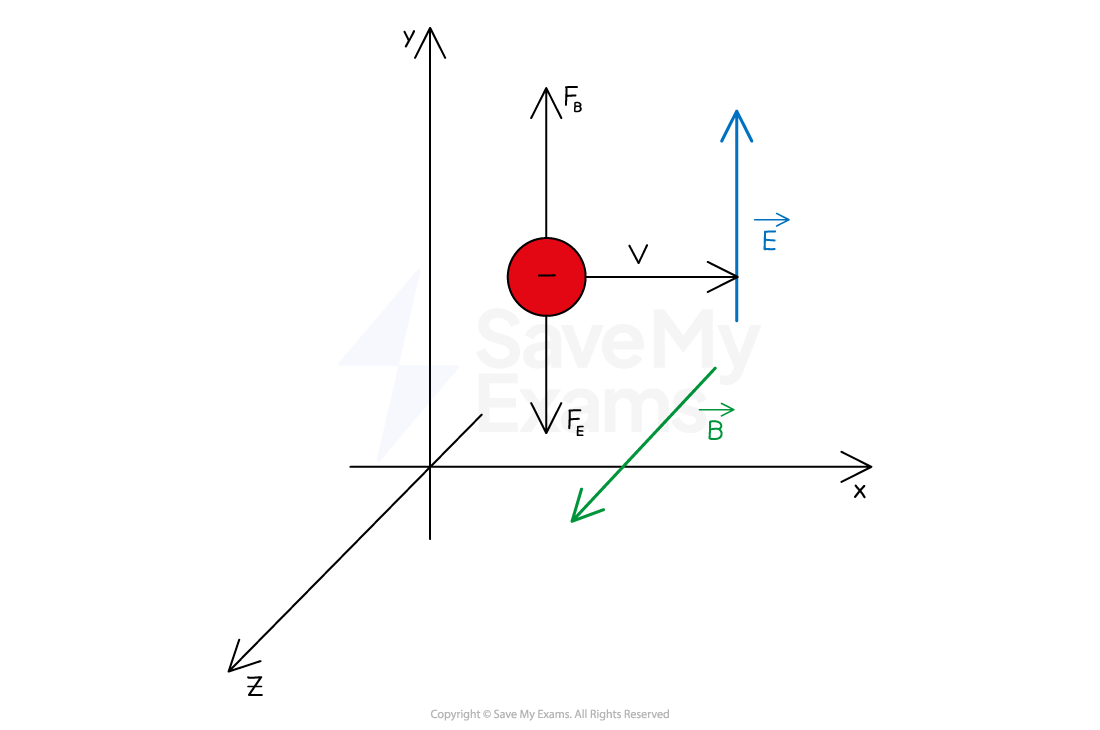
4-2-perpendicular-electric-and-magnetic-fields-with-forces-negative

The magnetic force acts up the page and the electric force acts in the opposite direction down the page

Balancing the Electric and Magnetic Fields

  • The field strengths of each field can be adjusted until the forces cancel each other out

  • If the magnitude of the electric and magnetic forces are equal, the particle will move in a straight line with constant speed

  • This speed can be determined by equating the two forces:

F subscript E space equals space F subscript B

  • Where:

    • The electric force on the particle:  F subscript E space equals space q E

    • The magnetic force on the particle:  F subscript B space equals space B q v

  • Equating these and rearranging for speed v gives:

q E space equals space B q v

v space equals space E over B

  • Therefore, the speed v is equal to the ratio of the electric and magnetic field strengths

Worked Example

An electron passes between two parallel metal plates moving with a constant velocity of 2.1 × 107 m s−1. The potential difference between the plates is 3100 V. A uniform magnetic field of magnitude 0.054 T acts perpendicular to the electric field and the movement of the electron. 

The electric field acts to the right and the electron is moving downwards.

(a) Determine the direction of the magnetic field

(b) Calculate the separation of the plates

 Answer:

(a) The direction of the magnetic field:

Step 1: Draw a diagram of the situation

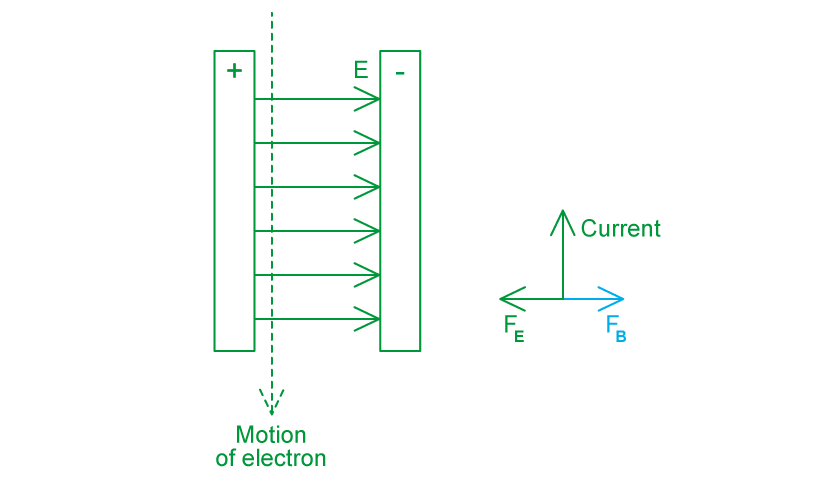
4-3-3-worked-example-ma

  • The electric field goes (from the positive plate to the negative plate), to the right

  • The electron is moving vertically downwards

  • So, the current is moving upwards in the opposite direction to the electron

  • The electric force is acting in the opposite direction to the electric field because the particle is an electron

Step 2: Determine the direction of the magnetic field

  • The electron is moving at a constant speed, so the magnetic and electric forces are equal and opposite

    • Hence, the magnetic force acts to the left 

(b) Calculate the separation of the plates:

Step 1: Calculate the magnitude of the electric field, E

v space equals space E over B space space space space space rightwards double arrow space space space space space E space equals space v B 

E space equals space open parentheses 2.1 space cross times space 10 to the power of 7 close parentheses space cross times space 0.054 space equals space 1.134 space cross times space 10 to the power of 6 space straight N space straight C to the power of negative 1 end exponent

Step 2: Calculate the separation of the plates

  • Use the electric field strength equation: 

E space equals space V over d space space space space space rightwards double arrow space space space space space d space equals space V over E

d space equals space fraction numerator 3100 over denominator 1.134 space cross times space 10 to the power of 6 end fraction

d space equals space 2.73 space cross times space 10 to the power of negative 3 end exponent m

Examiner Tips and Tricks

Take time to consider the direction of all components of the electric and magnetic fields.

Remember that the electric and magnetic forces act in the opposite direction for negatively charged particles compared to positively charged.

The direction of the charge in Fleming's left hand rule is always the direction of positive charge. This should be in the opposite direction if the particle has a negative charge!

Charge to Mass Ratio of Particles

  • The charge-to-mass ratio of a particle is defined as:

    The ratio of the total charge of a particle to its mass

  • It can be calculated using the equation:

charge-to-mass ratio = fraction numerator c h a r g e over denominator m a s s end fraction space equals space Q over m

  • The charge-to-mass ratio of an electron is e over m subscript e space equals space fraction numerator 1.60 cross times 10 to the power of negative 19 end exponent over denominator 9.11 cross times 10 to the power of negative 31 end exponent end fraction space equals space 1.76 cross times 10 to the power of 11 C kg−1

  • The charge-to-mass ratio of a proton is e over m subscript p space equals space fraction numerator 1.60 cross times 10 to the power of negative 19 end exponent over denominator 1.67 cross times 10 to the power of negative 27 end exponent end fraction space equals space 9.58 cross times 10 to the power of 7 C kg−1

Determining Charge-to-Mass Ratio

  • The charge-to-mass ratio of a charged particle can be determined by investigating its path in a uniform magnetic field

  • The method used by J.J. Thomson to determine the charge-to-mass ratio of an electron used:

    • 'Helmholtz coils' to generate a uniform magnetic field

    • oppositely charged parallel plates to generate a uniform electric field

Apparatus of the J.J. Thomson Experiment

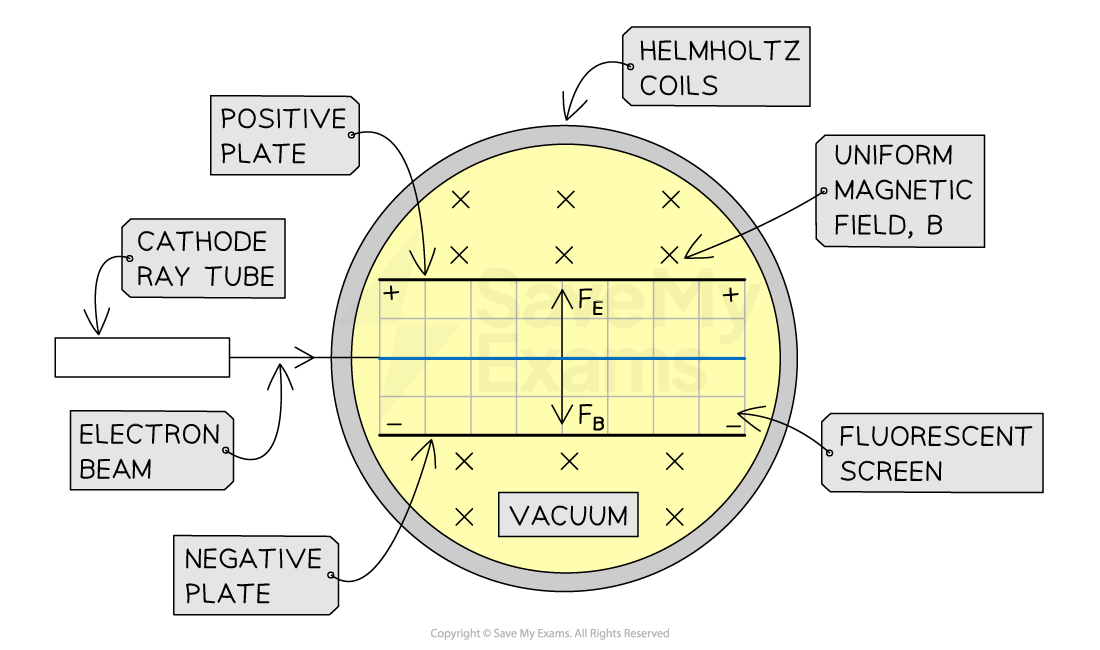
12-1-3-helmholtz

The magnetic field generates a downward force, the electric field between the plates generates an upward force - the fluorescent screen shows a straight beam when these two forces are equal and opposite

  • When moving in a magnetic field, a charge experiences a force perpendicular to its motion

    • From the diagram above, the magnetic field B is directed into the plane of the page

    • From Fleming's left-hand rule, the magnetic force FB on an electron acts downwards

  • When moving in a uniform electric field, a charge experiences a force towards either the positive or negative plate

    • The electrons are negative so they experience an upward electric force FE towards the positive plate

  • When these forces are equal in magnitude, the beam of electrons is horizontal and straight

E space equals space F over q space equals space V over d

  • The electric force can be adjusted by changing the potential difference V across the plates

  • Therefore, the upward electric force FE is equal to:

F subscript E space equals space fraction numerator q V over denominator d end fraction

  • Where:

    • q = charge of the particle (C)

    • V = potential difference between the plates (V)

    • d = separation between the plates (m)

  • The upward electric force is adjusted until it is equal to the downward magnetic force, making the electron beam horizontal:

F subscript E space equals space F subscript B

  • The downward magnetic force FB on the particle is equal to:

F subscript B space equals space B q v

  • Where:

    • v = speed of the particle (m s−1)

    • B = magnetic field strength (T)

  • Equating the two forces and rearranging for particle speed v:

B q v space equals space fraction numerator q V over denominator d end fraction

v space equals space fraction numerator V over denominator B d end fraction

  • If the electric field is switched off, the beam will be influenced by the magnetic field only

  • The particles will then travel in a circular path with the same speed v

Electron beam in a magnetic field

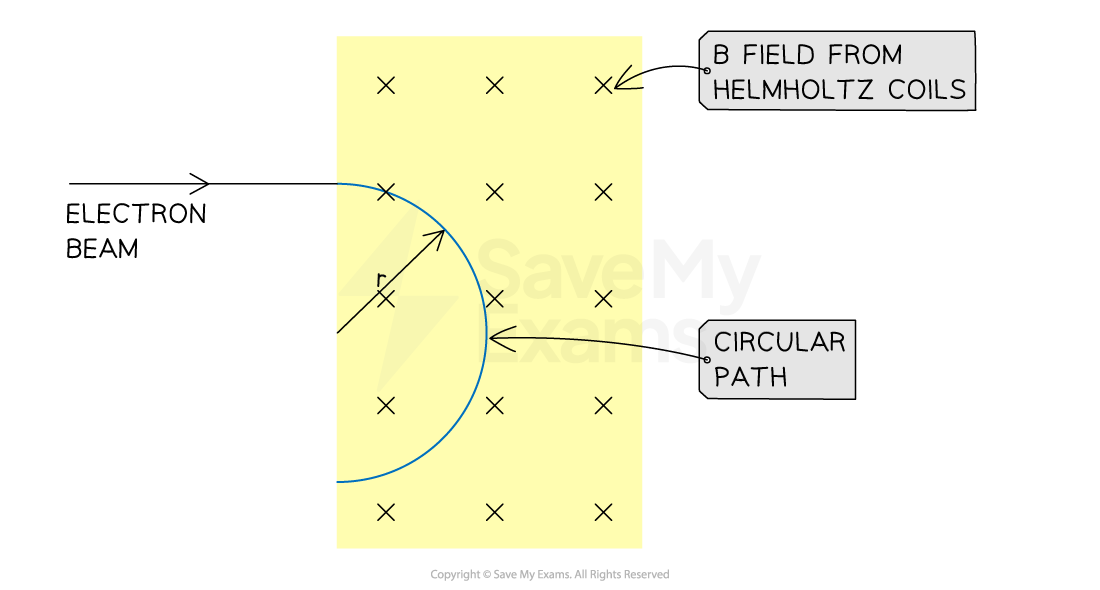
12-1-3-circular-path

The radius of the electron beam's circular path can be measured to calculate the charge-to-mass ratio of an electron

r space equals space fraction numerator m v over denominator B q end fraction

  • Where:

    • r = radius of the path (m)

    • m = mass of the particle (kg)

  • Rearranging for the charge-to-mass ratio:

q over m space equals space fraction numerator v over denominator r B end fraction

  • To measure these quantities:

    • the radius r of the path and the magnetic field strength B can be measured directly

    • the speed v of the particles can determined using perpendicular electric and magnetic fields

  • Combining these two equations gives an expression for the charge-to-mass ratio of a charged particle:

q over m space equals space fraction numerator 1 over denominator r B end fraction open parentheses fraction numerator V over denominator B d end fraction close parentheses space equals fraction numerator V over denominator r B squared d end fraction

  • Therefore, these four quantities open parentheses V comma space d comma space r comma space B close parentheses are needed to determine a particle's charge-to-mass ratio.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Charged Particles in Electric FieldsNext:Rutherford's Gold Foil Experiment
    Ann Howell

    Author: Ann Howell

    Expertise: Physics Content Creator

    Ann obtained her Maths and Physics degree from the University of Bath before completing her PGCE in Science and Maths teaching. She spent ten years teaching Maths and Physics to wonderful students from all around the world whilst living in China, Ethiopia and Nepal. Now based in beautiful Devon she is thrilled to be creating awesome Physics resources to make Physics more accessible and understandable for all students, no matter their schooling or background.