Revision NotesExam QuestionsFlashcardsPast Papers
IBPhysicsDPSLRevision NotesFieldsElectric & Magnetic FieldsCoulomb's Law

Coulomb's Law (DP IB Physics)

Revision Note

Ann Howell

Last updated

DP Physics: SLDP Physics: HL

Coulomb's Law

  • All charged particles generate an electric field

    • This field exerts a force on charged particles which are nearby

  • The electric force between two charges is defined by Coulomb’s law, which states that:

    The electric force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of their separation

  • This electric force can be calculated using the expression:

F space equals space k fraction numerator q subscript 1 q subscript 2 over denominator r squared end fraction

  • Where:

    • F = electric force (N)

    • q1, q2 = magnitudes of the charges (C)

    • r = distance between the centres of the two charges (m)

    • k = Coulomb constant (8.99 × 109 N m2 C–2)

  • Coulomb's law for two charges is analogous to Newton's law of gravitation for two masses

    • This means that electric and gravitational forces are very similar

    • For example, both forces follow an inverse square law with the separation between charge or mass

Electrostatic attraction between two charges

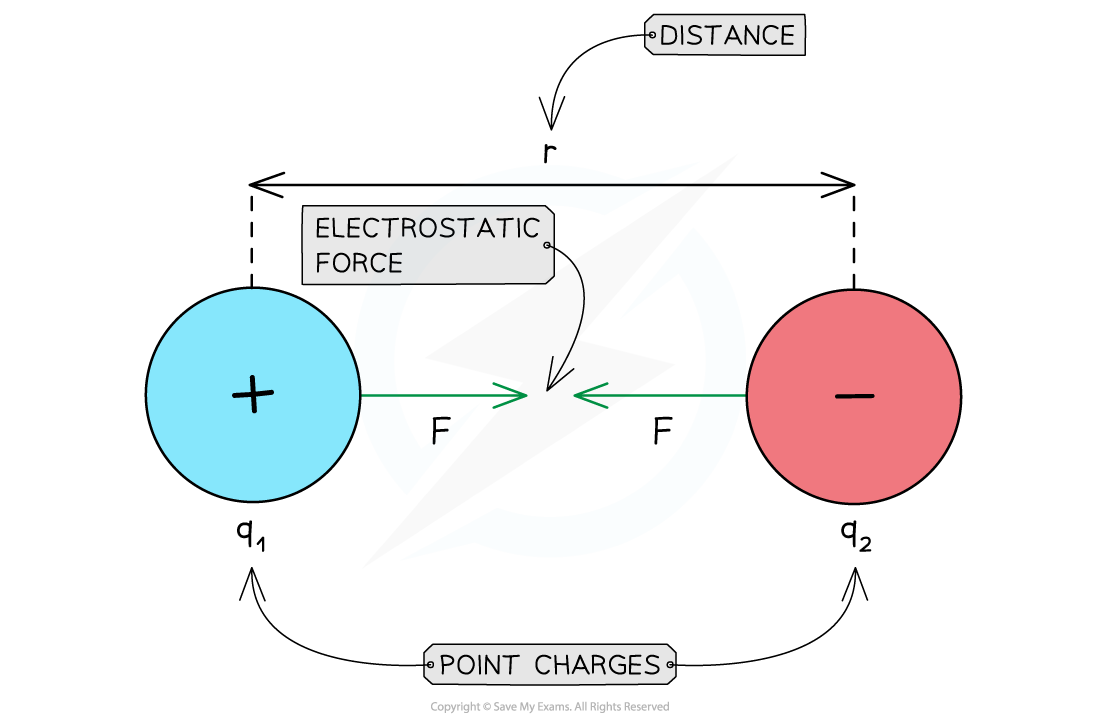
Coulomb's Law between Charges

The attractive electric force F between two point charges +q1 and −q2 with a separation of r is defined by Coulomb’s law

  • Coulomb's constant is given by:

k space equals space fraction numerator 1 over denominator 4 straight pi epsilon subscript italic 0 end fraction

  • Where ε0 is the permittivity of free space

    • ε0 = 8.85 × 10–12 C2 N–1 m–2 and refers to charges in a vacuum

    • The value of the permittivity of air is taken to be the same as ε0

    • All other materials have a higher permittivity ε > ε0

    • ε is a measure of the resistance offered by a material in creating an electric field within it

  • The value of k depends on the material between the charges

    • In a vacuum, k = 8.99 × 109 N m2 C–2

Repulsive & Attractive Forces 

  • Unlike the gravitational force between two masses which is only attractive, electric forces can be attractive or repulsive

  • Between two charges of the same type: 

    • The product q1q2 is positive, so the forces have positive signs

    • Positive forces mean the charges experience repulsion

  • For two opposite charges:

    • The product q1q2 is negative, so the forces have negative signs

    • Negative forces mean the charges experience attraction

Worked Example

An alpha particle is placed 2.0 mm from a gold nucleus in a vacuum.

Taking them as point charges, calculate the magnitude of the electric force acting between the nuclei.

  • Proton number of helium = 2

  • Proton number of gold = 79

Answer:

Step 1: Write down the known quantities

  • Separation between charges, r = 2.0 mm = 2.0 × 10–3 m

  • Elementary charge, e = 1.60 × 10–19 C (from the data booklet)

  • Coulomb constant, k = 8.99 × 109 N m2 C–2 (from the data booklet)

Step 2: Calculate the charges of the alpha particle and gold nucleus 

  • An alpha particle (helium nucleus) has 2 protons, hence it has a charge of:

q1 = 2e = 2 × (1.60 × 10–19)

  • A gold nucleus has 79 protons, hence it has a charge of:

q2 = 79e = 79 × (1.60 × 10–19)

Step 3: Write down Coulomb's law

F space equals space k fraction numerator q subscript 1 q subscript 2 over denominator r squared end fraction

Step 4: Substitute the values and calculate the magnitude of the electric force

F space equals space open parentheses 8.99 cross times 10 to the power of 9 close parentheses cross times fraction numerator 2 cross times 79 cross times open parentheses 1.60 cross times 10 to the power of negative 19 end exponent close parentheses squared over denominator open parentheses 2.0 cross times 10 to the power of negative 3 end exponent close parentheses squared end fraction space equals space 9.1 cross times 10 to the power of negative 21 end exponent N (2 s.f.)

Examiner Tips and Tricks

You do not need to memorise the numerical value of the Coulomb's constant k or that of the permittivity of free space ε0. They will both be given in the data booklet.

Unless specified in the question, you should assume that charges are located in a vacuum.

You should note that Coulomb's law can only be applied to charged spheres whose size is much smaller than their separation. Only in this case, the point charge approximation is valid. You must remember that the separation r must be taken from the centres of the spheres.

You cannot use Coulomb's law to calculate the electrostatic force between charges distributed on irregularly-shaped objects.

Different Values of Permittivity

  • Permittivity is the measure of how easy it is to generate an electric field in a certain material

  • The relativity permittivity εr is sometimes known as the dielectric constant

  • For a given material, it is defined as:

    The ratio of the permittivity of a material to the permittivity of free space

  • Relativity permittivity can be expressed as:

epsilon subscript r space equals space epsilon over epsilon subscript 0

  • Where:

    • εr = relative permittivity

    • ε = permittivity of a material (F m−1)

    • ε0 = permittivity of free space (F m−1)

  • Relative permittivity has no units because it is a ratio of two values with the same unit

  • When there is a material between two charges, the Coulomb constant becomes

k space equals space fraction numerator 1 over denominator 4 straight pi epsilon end fraction

  • In air, the relative permittivity is 1, so epsilon space equals space epsilon subscript 0

  • In other materials, the Coulomb constant reduces as epsilon space equals space epsilon subscript r epsilon subscript 0

Examples of Relative Permittivity

  • Some values of relative permittivity for different insulators are shown in the table below:

Material

Relative Permittivity, εr

free space (vacuum)

1

air

1.00054

paper

4

polystyrene

3

ceramic

100 - 15 000

paraffin

2.3

pure water

80

Worked Example

Calculate the permittivity of a material that has a relative permittivity of 4.5 × 1011. State an appropriate unit for your answer.

Answer:

Step 1: Write down the relative permittivity equation

epsilon subscript r space equals space epsilon over epsilon subscript 0

Step 2: Rearrange for permittivity of the material ε

epsilon space equals space epsilon subscript r epsilon subscript 0

Step 3: Substitute the values and calculate

epsilon space equals space open parentheses 4.5 cross times 10 to the power of 11 close parentheses cross times open parentheses 8.85 cross times 10 to the power of negative 12 end exponent close parentheses space equals space 3.98 space equals space 4.0 F m−1 (2 s.f.)

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Static ElectricityNext:Electric Field Strength
    Ann Howell

    Author: Ann Howell

    Expertise: Physics Content Creator

    Ann obtained her Maths and Physics degree from the University of Bath before completing her PGCE in Science and Maths teaching. She spent ten years teaching Maths and Physics to wonderful students from all around the world whilst living in China, Ethiopia and Nepal. Now based in beautiful Devon she is thrilled to be creating awesome Physics resources to make Physics more accessible and understandable for all students, no matter their schooling or background.