Centripetal Force (DP IB Physics: SL)

• An object moving in a circle is not in equilibrium, it has a resultant force acting upon it
  • This is known as the centripetal force and is what keeps the object moving in a circle

• The centripetal force (F) is defined as:

The resultant force perpendicular to the velocity, and therefore directed towards the centre of the circle, required to keep a body in uniform circular motion

•  The magnitude of the centripetal force F can be calculated using:

Centripetal force is always perpendicular to the linear velocity (i.e., the direction of travel)

• Where:
  • F = centripetal force (N)
  • v = linear speed (m s⁻¹)
  • ⍵ = angular speed (rad s⁻¹)
  • r = radius of the orbit (m)

• Note: centripetal force and centripetal acceleration act in the same direction
  • This is due to Newton's Second Law

• The centripetal force is not a separate force of its own
• It can be any type of force, depending on the situation, which keeps an object moving in a circular path
  • For example, tension, friction, gravitational, electrical or magnetic

Examples of centripetal force

• When solving circular motion problems involving one of these forces, the equation for centripetal force can be equated to the relevant force equation
• For example, for a charged particle travelling in a circle, the centripetal force causing the charged particle to move in a circle is provided by the magnetic force
• Therefore, equating the expressions for centripetal force and magnetic force gives the following:

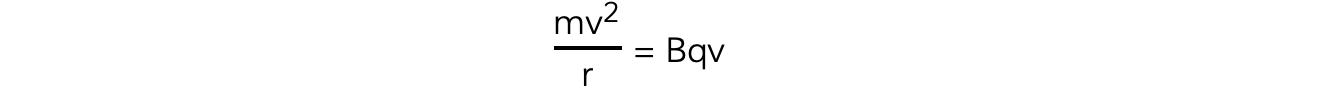
• Where:
  • B = magnetic field strength (T)
  • q = charge on the particle (C)
  • m = mass of the particle (kg)
  • v = speed of the particle (m s⁻¹)
  • r = radius of orbit (m)

Step 1: Draw the forces on the bucket at the top

Step 2: Calculate the centripetal force

• • The weight of the bucket = mg
  • This is equal to the centripetal force since it is directed towards the centre of the circle

Step 3: Rearrange for velocity v

• • m cancels from both sides

Step 4: Substitute in values