I-V Characteristics (DP IB Physics): Revision Note
Ohm's Law
Ohm's law states that:
For a component at a constant temperature, the current through it is proportional to the potential difference across it
It is defined by the equation:
Where:
V = potential difference (V)
I = current (A)
R = resistance (Ω)
An electrical component obeys Ohm’s law if its graph of current against potential difference is a straight line through the origin
A fixed resistor obeys Ohm’s law i.e. it is an ohmic component
A filament lamp does not obey Ohm’s law i.e. it is a non-ohmic component
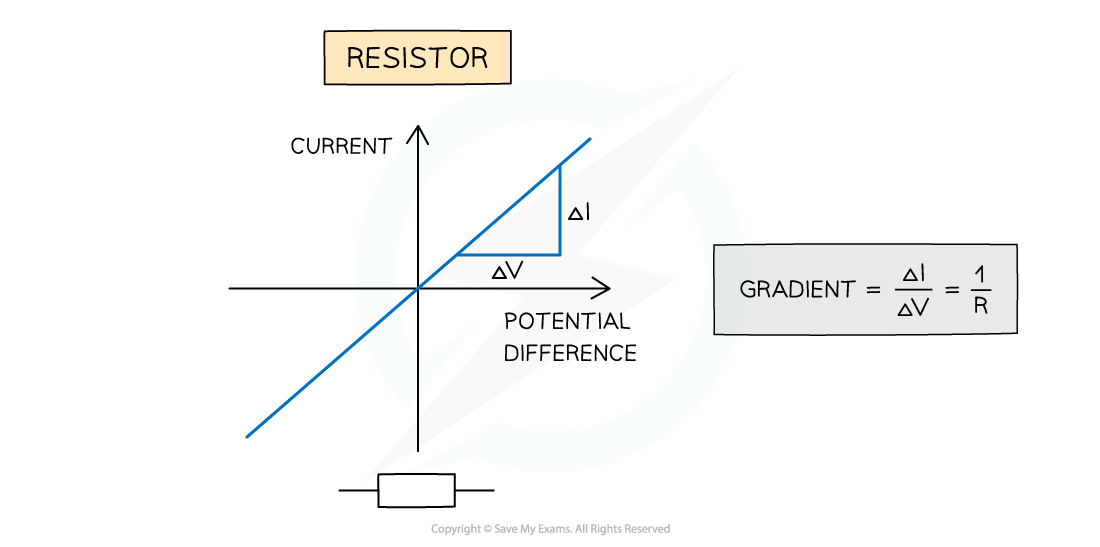
The current-voltage graph for a fixed resistor is a straight line through the origin. The fixed resistor is an ohmic component
The resistance of an ohmic component can be calculated from the gradient of a current-voltage graph, since resistance is equal to
If current
is on the y-axis and potential difference
is on the x-axis, then
If potential difference
is on the y-axis and current
is on the x-axis, then
Any metal conductor at a constant temperature can be considered an ohmic device
This is likely to be a fixed resistance
Non-ohmic devices include:
Lamps
LEDs
Thermistors
Worked Example
The current flowing through a component varies with the potential difference V across it as shown.

Which graph best represents how the resistance R varies with V?

Answer: D
Step 1: Write down the equation for the resistance R
Step 2: Link the resistance to the gradient of the graph
Step 3: Identify the gradient of different sections of the graph and use it to deduce what happens to the resistance
The first straight section of the graph has a constant gradient
So the resistance remains constant
The second section is curved and the steepness of the line increases, so the gradient increases
So the resistance decreases
Step 4: Identify the correct graph out of the four proposed
Constant resistance is indicated by a straight horizontal line
So either C or D are correct
Decreasing resistance is indicated by a line curving downwards
So only D is correct
Examiner Tips and Tricks
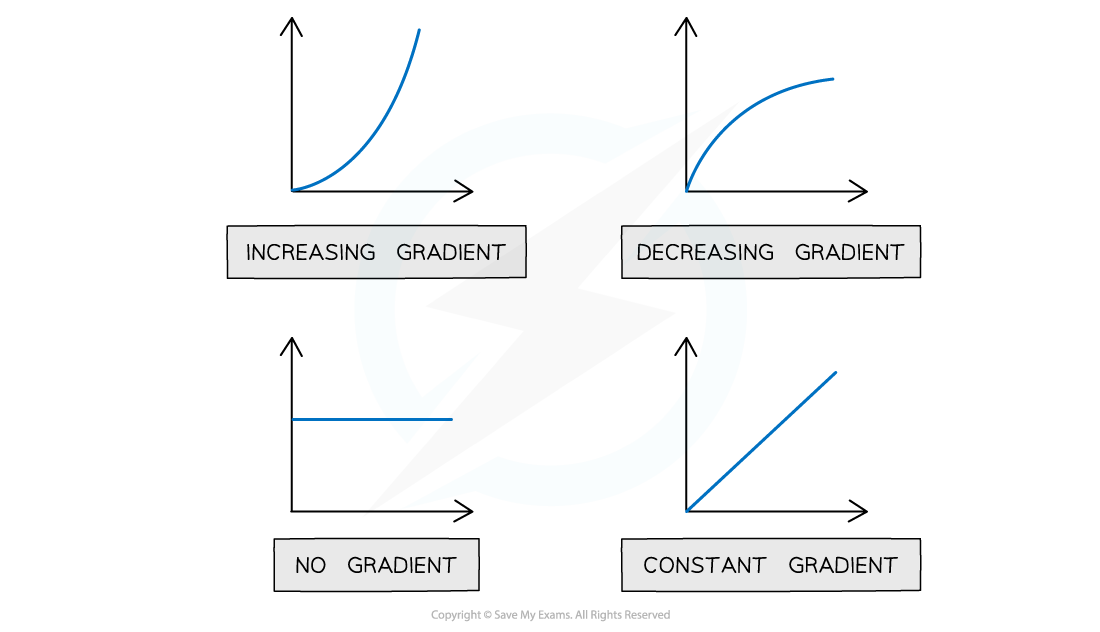
When solving problems about Ohm's law you will often deal with graphs. You need to be confident in identifying and calculating their gradients.
In maths, the gradient is the slope of the graph (i.e.
)
The graphs below show a summary of how the slope of the graph represents the gradient
Although the Ohm's law equation is not given on your data sheet, you can see it is just rearranging to make V the subject.
I-V Characteristics
The Ohmic and non-Ohmic behaviour of an electrical conductor can be deduced by looking at its I-V (current-voltage) characteristics
This is usually plotted as a graph showing the variation of current against voltage
The relation between potential difference across an electrical component (e.g. a fixed resistor) and current can be investigated through a circuit such as the one below

Circuit for plotting graphs of current against voltage. The component being investigated here is a fixed resistor
By adjusting the resistance on the variable resistor:
The current in the circuit will change
For each value of the current
, the potential difference
can be recorded
A graph of current against potential difference can then be plotted
I-V characteristics of common conductors
Common ohmic conductors include
Wires (at constant temperature)
Resistors
Common non-ohmic conductors include
Semiconductor diodes e.g. LEDs
Filament lamp
Thermistors & light-dependent resistors (LDRs)
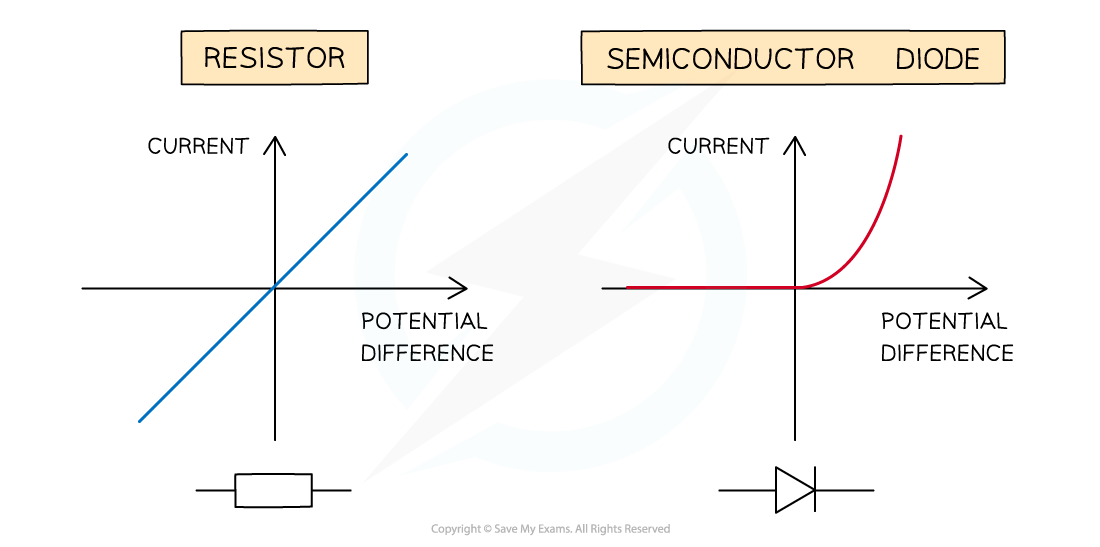
I–V characteristics for an ohmic conductor (e.g. resistor) and semiconductor diode (e.g. LED)
Resistor
A resistor is an example of an Ohmic resistor
This means the current is directly proportional to the potential difference
Its I-V graph is a straight line through the origin
Semiconductor Diode
When the current is in the direction of the arrowhead symbol, the diode is said to be forward-biased
There is a sharp increase in current
This is shown on the right side of the graph
When the diode is switched around, it does not conduct and it is said to be reverse biased
The current through the diode is zero
This is shown on the left side of the graph
The diode is a non-ohmic component
Its I-V graph is not a straight line through the origin
A specific type of diode is an LED
The I-V characteristic graphs looks the exact same for this
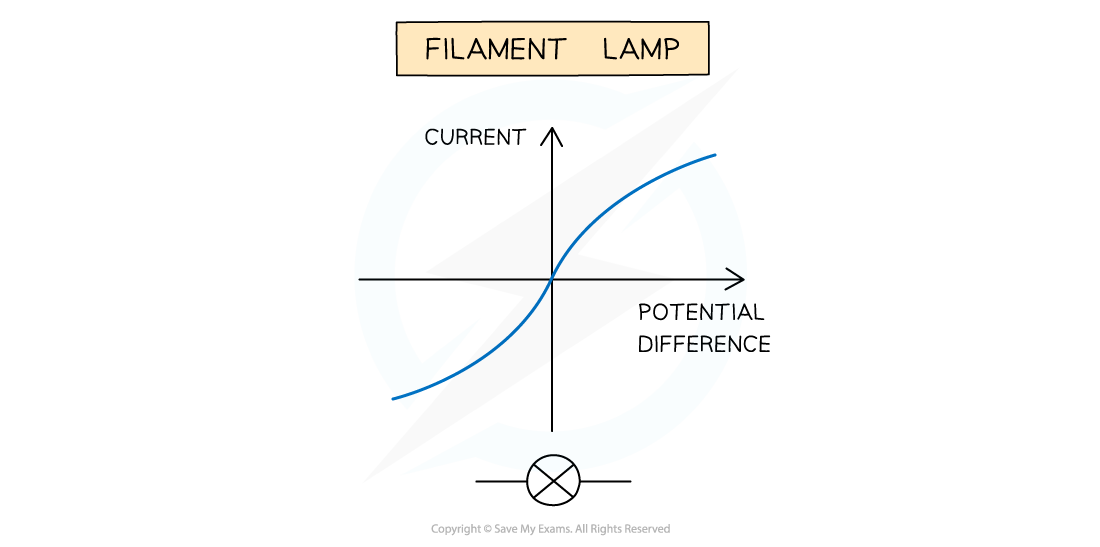
I–V characteristics for a filament lamp
Filament Lamp
For very small voltages, the filament lamp behaves as an ohmic component
The middle section of the graph (around zero voltage) is straight and passes through the origin
As voltage increases:
More current flows through the filament lamp and the temperature of the filament in the lamp increases
The higher the temperature of the filament, the higher its resistance
Since resistance opposes current, the current flows through the filament at a slower rate
This is shown by the curved section of the graph
For slightly higher voltages, the filament lamp is non-ohmic
The I-V graph is a curve with decreasing gradient
Examiner Tips and Tricks
Make sure you're confident in drawing the I–V characteristics for different components, as you may be asked to sketch these from memory or to identify those given in exam questions

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
