Amplitude & Intensity

Intensity

The intensity of a wave is defined as follows:

Power per unit area

Intensity is measured in W m^–2

Power is defined as:

The rate of energy transfer

Therefore, intensity can also be defined as:

The rate of energy transfer per unit area

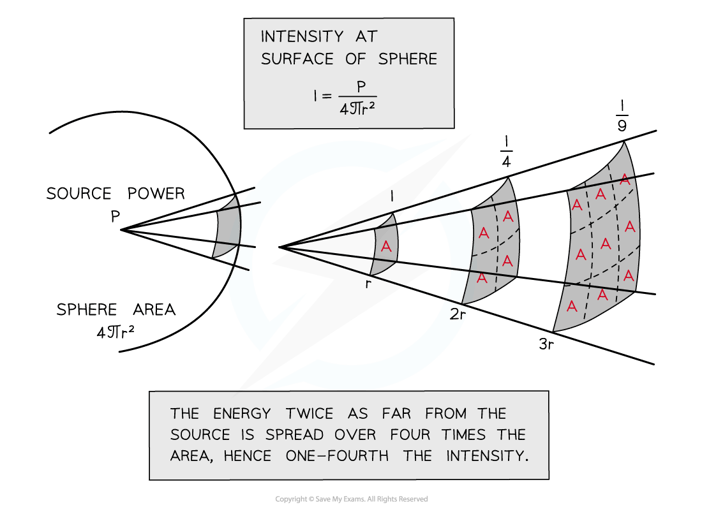
For spherical waves being emitted by a point source equally in all directions, the intensity follows an inverse square law with distance from the point source

$I \propto \frac{1}{r^{2}}$

Where:
- I = intensity of the wave in watts per metre squared (W m^–2)
- r = distance from the point source in metres (m)

For spherical waves being emitted by a point source equally in all directions, the intensity at the surface of a sphere is calculated using:

I = $\frac{P}{4 π r^{2}}$

Where:
- P = power in watts (W)
- r = radius of sphere in metres (m)
For spherical waves being emitted by a point source equally in all directions, the power is a constant, therefore the relationship can be expressed as:

I ∝ $\frac{1}{r^{2}}$

This is an example of an inverse square law relationship

I ∝ x⁻²

7117-intensity-of-a-spherical-wave

Intensity decreases by the inverse square law

Intensity Variation with Amplitude

By definition, the intensity of a wave (its power per unit area) is proportional to the energy transferred by the wave
The intensity of a wave at a particular point is related to the amplitude of the wave at that point
The energy transferred by a wave is proportional to the square of the amplitude
Therefore, the intensity of a wave is proportional to the square of the amplitude

$I \propto A^{2}$

Where:
- I = intensity of the wave in W m^–2
- A = amplitude of the wave in metres (m)

Worked example

A person stands 10 m away from a loudspeaker. The sound produced by the loudspeaker is very loud, so the person moves 20 m away from it.

State the effect of this change on the intensity and the amplitude of the sound waves heard by the person.

Step 1: Write down the known quantities

- Original distance, r₁ = 10 m
- New distance, r₂ = 20 m

Step 2: Write down the relationship between the intensity of a wave and the distance from the point source producing the wave

Step 2: State the new intensity

- Since the distance doubles (r₂ = 2r₁), the intensity is reduced by a factor four

Step 3: Write down the relationship between the intensity of a wave and its amplitude

Step 4: State the new amplitude

- Since the intensity is reduced by a factor four, the amplitude decreases by half

Amplitude & Intensity (DP IB Physics: SL)

Revision Note

Intensity

Intensity Variation with Amplitude

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

1. Measurement & Uncertainties

1.1 Measurements in Physics

1.1.1 SI Units

1.1.2 Using Scientific Notation

1.1.3 Estimating Physical Quantities

1.2 Uncertainties & Errors

1.2.1 Random & Systematic Errors

1.2.2 Calculating Uncertainties

1.2.3 Determining Uncertainties from Graphs

1.3 Vectors & Scalars

1.3.1 Vector & Scalar Quantities

1.3.2 Combining & Resolving Vectors

1.3.3 Solving Vector Problems

2. Mechanics

2.1 Motion

2.1.1 Distance & Displacement

2.1.2 Speed & Velocity

2.1.3 Acceleration

2.1.4 Graphs Describing Motion

2.1.5 Uniform Acceleration

2.1.6 Acceleration of Free Fall Experiment

2.1.7 Projectile Motion

2.1.8 Terminal Speed

2.2 Forces

2.2.1 Free-Body Diagrams

2.2.2 Newton’s First Law

2.2.3 Newton’s Second Law

2.2.4 Newton’s Third Law

2.2.5 Applying Newton’s Laws of Motion

2.2.6 Friction

2.3 Work, Energy & Power

2.3.1 Kinetic Energy

2.3.2 Gravitational Potential Energy

2.3.3 Elastic Potential Energy

2.3.4 Work Done

2.3.5 Power

2.3.6 Principle of Conservation of Energy

2.3.7 Efficiency

2.4 Momentum & Impulse

2.4.1 Force & Momentum

2.4.2 Impulse

2.4.3 Conservation of Linear Momentum

2.4.4 Collisions & Explosions

3. Thermal Physics

3.1 Thermal Concepts

3.1.1 Solids, Liquids & Gases

3.1.2 Temperature

3.1.3 Internal Energy

3.1.4 Specific Heat Capacity

3.1.5 Specific Latent Heat

3.1.6 Phase Change

3.1.7 Investigating Thermal Energy

3.2 Modelling a Gas

3.2.1 Ideal Gas Laws

3.2.2 Ideal Gas Equation

3.2.3 Kinetic Model of an Ideal Gas

3.2.4 Mole Calculations

3.2.5 Investigating Gas Laws

4. Waves

4.1 Oscillations

4.1.1 Properties of Oscillations

4.1.2 Simple Harmonic Oscillations

4.1.3 SHM Graphs

4.1.4 Energy in SHM

4.2 Travelling Waves

4.2.1 Properties of Waves

4.2.2 Transverse & Longitudinal Waves

4.2.3 Electromagnetic Waves

4.2.4 Sound Waves

4.3 Wave Characteristics

4.3.1 Wavefronts

4.3.2 Amplitude & Intensity

4.3.3 Superposition