Electromagnetic Waves (DP IB Physics: SL)

• An electromagnetic wave is generated by the combined oscillation of an electric and a magnetic field
• These fields oscillate perpendicular to each other and to the direction of motion of the wave (i.e. the direction in which energy is transferred)

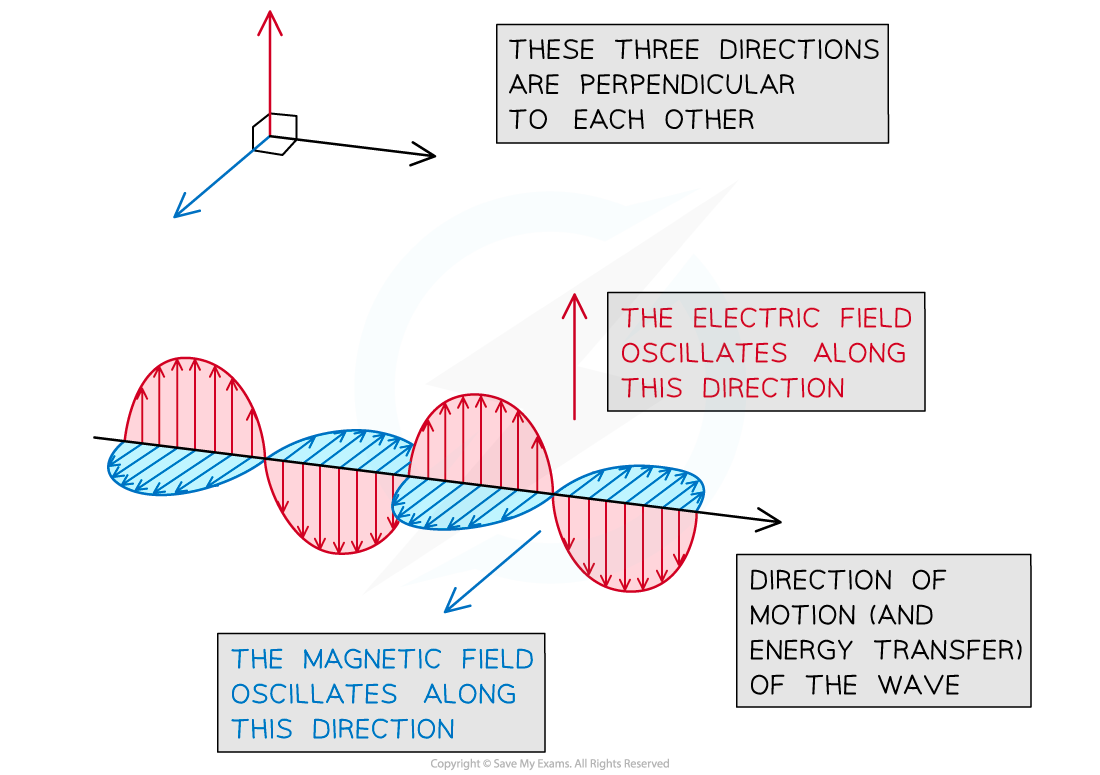
An electromagnetic wave is generated by the combined oscillation of an electric and a magnetic field

• Electromagnetic waves are transverse waves and, as such, they can travel through vacuum
• Regardless of their frequency, all electromagnetic waves travel at the speed of light c = 3 × 10⁸ m s^–1 in vacuum
• Electromagnetic waves form a continuous spectrum based on their frequency

The electromagnetic spectrum

• Humans can only sense electromagnetic waves with wavelengths in the range 700 nm - 400 nm, which are the limits of the so-called visible spectrum 
• Electromagnetic waves with longer and shorter wavelengths are invisible to the human eye

• Knowing the wavelengths of electromagnetic waves, their frequencies can be calculated using the wave equation, and remembering that their speed in vacuum is always equal to the speed of light

Step 1: Write down the known quantities 

• • Note that you must convert the values of the wavelength from nanometres (nm) into metres (m)

• • • λ_lower = 450 nm = 4.5 × 10^–7 m
    • λ_higher = 490 nm = 4.9 × 10^–7 m

Step 2: Remember that all electromagnetic waves travel at the speed of light in vacuum

• • From the data booklet, c = 3 × 10⁸ m s^–1

Step 3: Write down the wave equation 

c = fλ

Step 4: Rearrange the above equation to calculate the frequency f 

Step 5: Substitute the lower and higher values of the wavelength to calculate the limiting values of the frequency of blue light 

• • The lower frequency f_lower corresponds to the higher value of the wavelength λ_higher

              = 6.1 × 10¹⁴ Hz

• • The higher frequency f_higher corresponds to the lower value of the wavelength λ_lower

              = 6.7 × 10¹⁴ Hz

Step 6: Write down the range of frequencies of blue light 

f = 6.1 × 10¹⁴ Hz - 6.7 × 10¹⁴ Hz