Kinetic Theory of Gases (DP IB Physics): Revision Note
Kinetic Theory of Gases
Ideal gases are described in terms of the kinetic theory
This is a modelled system used to approximate the behaviour of real gases
A gas consists of atoms or molecules moving around randomly at high speeds
The kinetic theory of gases models the thermodynamic behaviour of gases by linking:
The microscopic properties of particles e.g. mass and speed
The macroscopic properties of particles e.g. pressure and volume
Kinetic theory and ideal gases are based on a set of the following assumptions:
A gas consists of many identical molecules in a container. They all have the same mass
The volume of the molecules is negligible compared to the volume of the container. This means they can be considered point particles
The molecules are in continuous random motion at high speeds
The molecules obey Newton's laws of motion
The molecules collide elastically with each other and the walls of the container
There are no intermolecular forces between the molecules except during collisions
The time of a collision between molecules is negligible compared to the time between collisions
External forces (e.g. gravity) are ignored
The number of molecules of gas in a container is very large. Therefore the average behaviour (eg. speed) is usually considered
Each particle exerts a force on the wall of the container with which it collides. This means the average of the forces produced by all gas particles results in a uniform gas pressure
Real & Ideal Gases
Real gases will not always obey the ideal gas equation
This is because the assumptions of the kinetic theory of gases may not always be valid
For example, the assumption that there are no intermolecular forces between gas molecules is not particularly realistic
However, under certain conditions, they can be considered ideal gases
An ideal gas is a good approximation of a real gas when:
The gas pressure is low
The gas density is low
Temperature is sufficiently higher than the boiling point of the substance
At very high pressures, densities and low temperatures, real gases do not obey the kinetic theory model
This is because at high pressures and densities:
Molecules are closer together
Therefore, there will be attractive forces between the molecules
The volume of the molecules cannot be considered negligible due to the high density
At low temperatures:
A gas can change into a liquid, so the substance will no longer behave like a gas
No gas is completely ideal, but air at normal room temperature and pressure, based on experiments, behaves very similar to an ideal gas
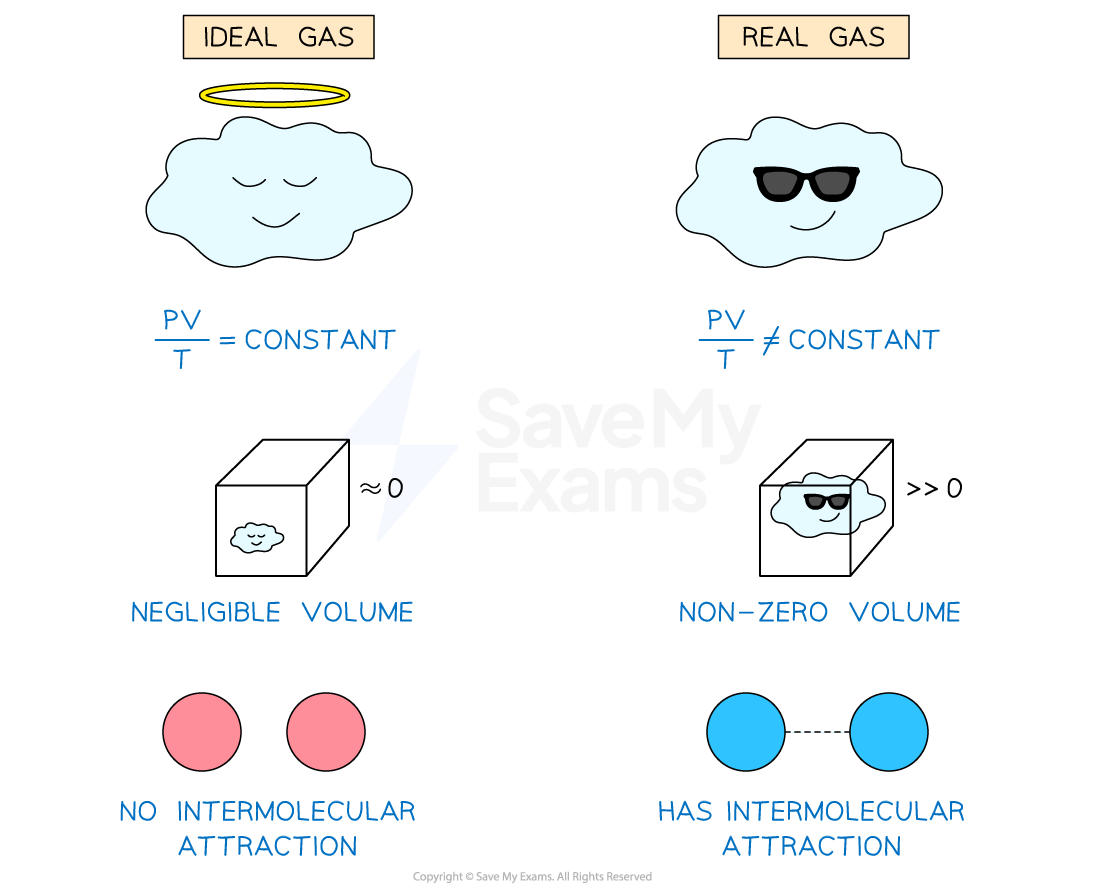
Real vs. ideal gases

Unlock more, it's free!
Did this page help you?