Determining Uncertainties from Graphs (DP IB Physics: SL)

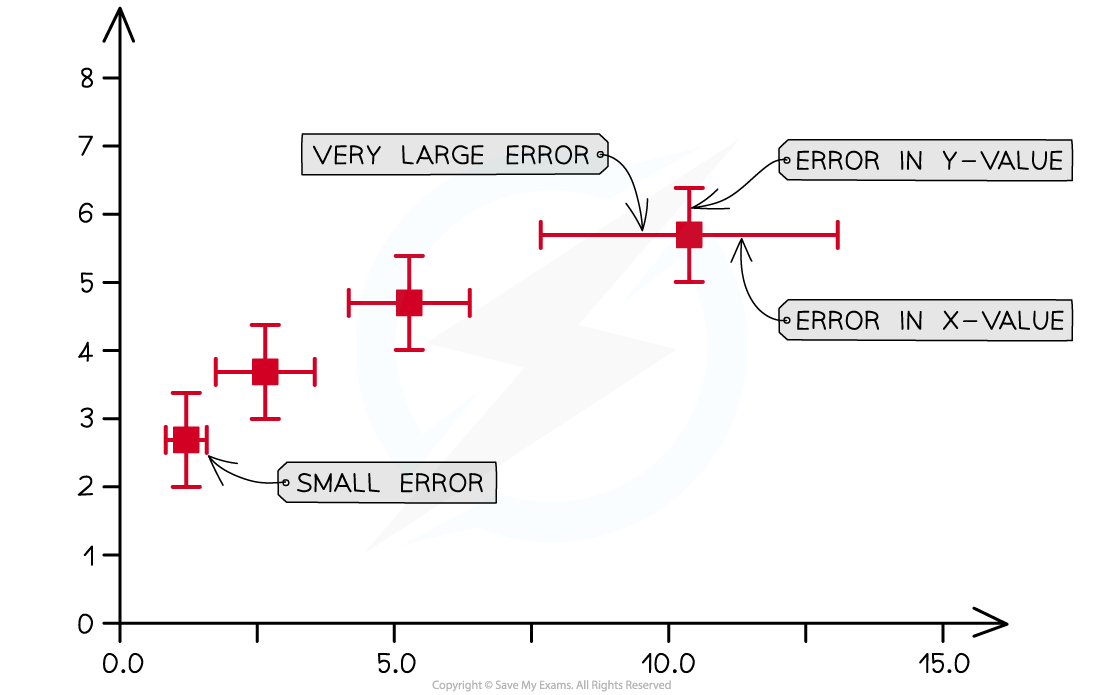
• The uncertainty in a measurement can be shown on a graph as an error bar
• This bar is drawn above and below the point (or from side to side) and shows the uncertainty in that measurement
• Error bars are plotted on graphs to show the absolute uncertainty of values plotted

Representing error bars on a graph

• To calculate the uncertainty in a gradient, two lines of best fit should be drawn on the graph:
  • The ‘best’ line of best fit, which passes as close to the points as possible
  • The ‘worst’ line of best fit, either the steepest possible or the shallowest possible line which fits within all the error bars

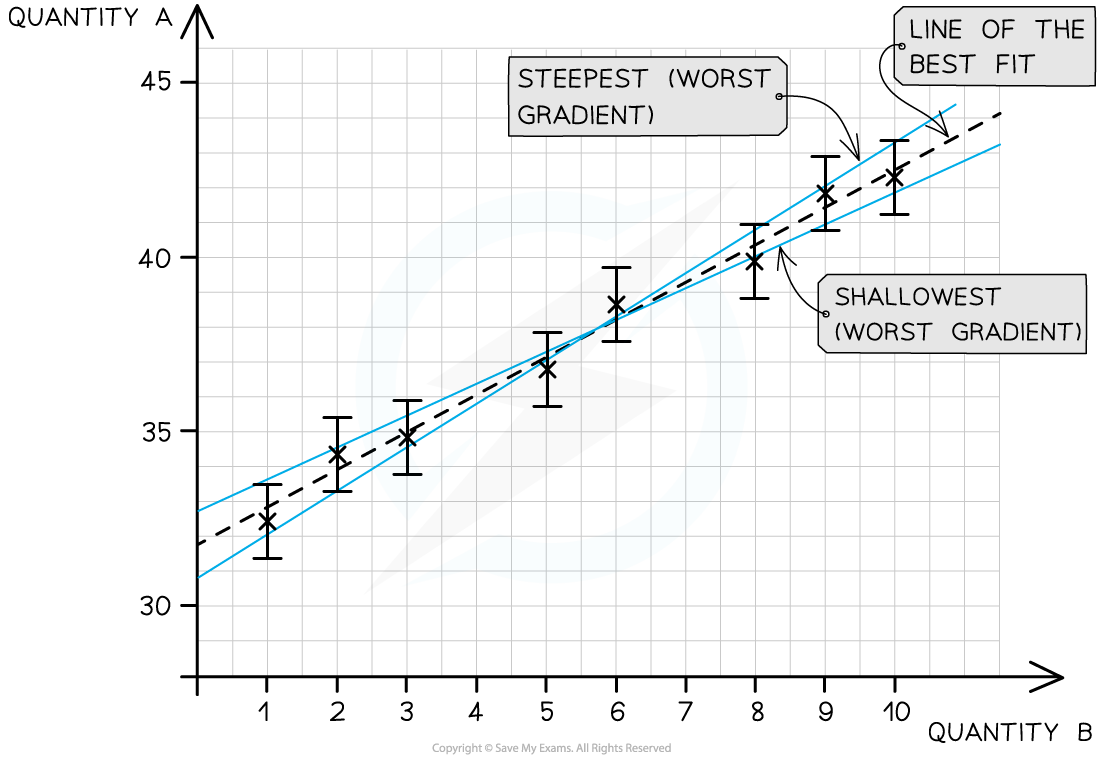
The line of best fit passes as close as possible to all the points. The steepest and shallowest lines are known as the worst fit

• The percentage uncertainty in the gradient can be found using the magnitude of the 'best' and 'worst' gradients:

percentage uncertainty = 

• Either the steepest or shallowest line of best fit may have the 'worst' gradient on a case-by-case basis.
  • The 'worst' gradient will be the one with the greatest difference in magnitude from the 'best' line of best fit.
  • The equation above is for the case where the 'worst' gradient is the shallowest.
  • If the 'worst' gradient is the steepest, then the 'worst' gradient should be subtracted from the 'best' gradient and then divided by the best gradient and multiplied by 100

• Alternatively, the average of the two maximum and minimum lines can be used to calculate the percentage uncertainty:

percentage uncertainty =

• The percentage uncertainty in the y-intercept can be found using:

percentage uncertainty = 

percentage uncertainty =

Percentage Difference

• The percentage difference gives an indication of how close the experimental value achieved from an experiment is to the accepted value
  • It is not a percentage uncertainty

• The percentage difference is defined by the equation:

percentage difference =

• The experimental value is sometimes referred to as the 'measured' value
• The accepted value is sometimes referred to as the 'true' value
  • This may be labelled on a component such as the capacitance of a capacitor or the resistance of a resistor
  • Or, from a reputable source such as a peer-reviewed data booklet

• For example, the acceleration due to gravity g is known to be 9.81 m s^–2. This is its accepted value
  • From an experiment, the value of g may be found to be 10.35 m s^–2
  • Its percentage difference would therefore be 5.5 %

• The smaller the percentage difference, the more accurate the results of the experiment

Step 1: Draw sensible scales on the axes and plot the data

Step 2: Draw the errors bars for each point

Step 3: Draw the line of best fit

Step 4: Draw the line of worst fit

Step 5: Work out the gradient of each line and calculate the percentage uncertainty