Equations for Simple Harmonic Motion (SHM) (DP IB Physics): Revision Note
Equations for Simple Harmonic Motion
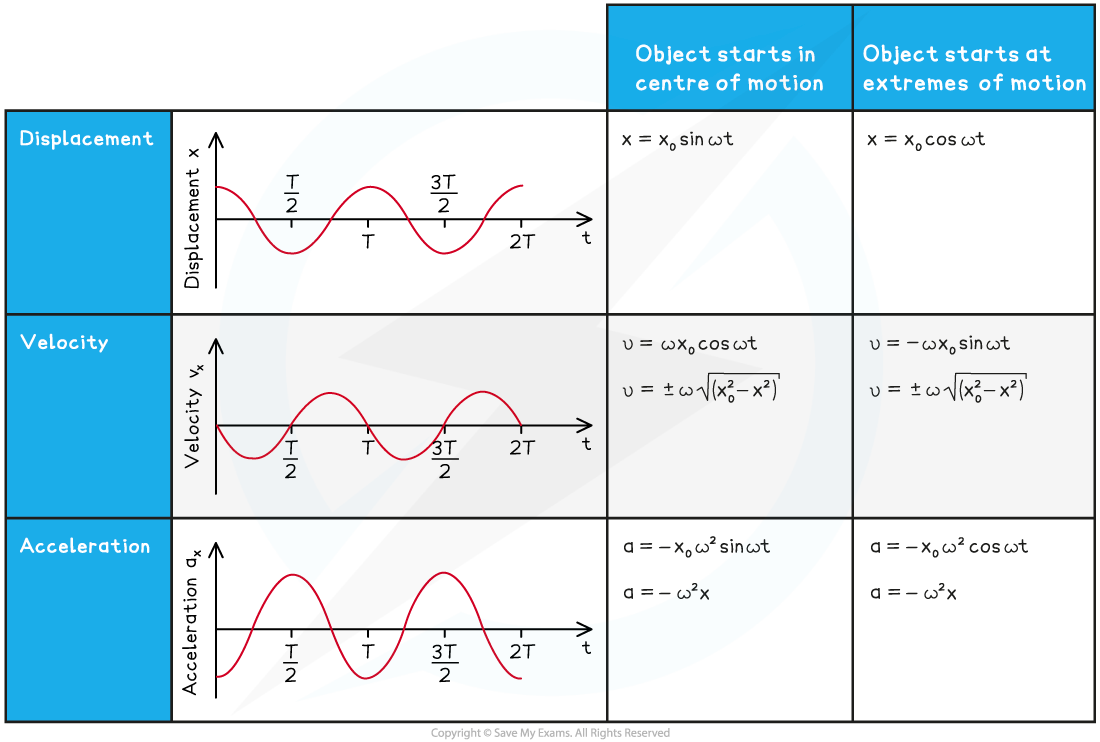
Summary of SHM Equations
For a body that begins oscillating from its equilibrium position (i.e.
when
), its displacement, velocity and acceleration can be described by the equations:
For a body that begins oscillating from its amplitude position (i.e.
when
), its displacement, velocity and acceleration can be described by the equations:
The variation of an oscillator's velocity with its displacement x is defined by:
This equation shows that the larger the amplitude
of an oscillation, the greater the distance it must travel in a given time period
Hence, the faster it travels, the closer it is to the equilibrium position
In the above equations, the variables are as follows:
= displacement of the oscillator (m)
= maximum displacement, or amplitude (m)
= velocity of the oscillator (m s−1)
= acceleration of the oscillator (m s−2)
= angular frequency (rad s−1)
= time (s)
Summary table of equations and graphs for displacement, velocity and acceleration
The Origin of the Displacement Equations
The SHM displacement equation for an object oscillating from its equilibrium position (x = 0 at t = 0) is:
Where:
Φ = phase difference (radians) = 0
Because:
The graph of x = sin (t) starts from amplitude x0 = 0 when the pendulum is in the equilibrium position at t = 0
The displacement is at its maximum when sin(⍵t) equals 1 or −1, when x = x0
Use the IB revision notes on the graphs of trigonometric functions to aid your understanding of trigonometric graphs
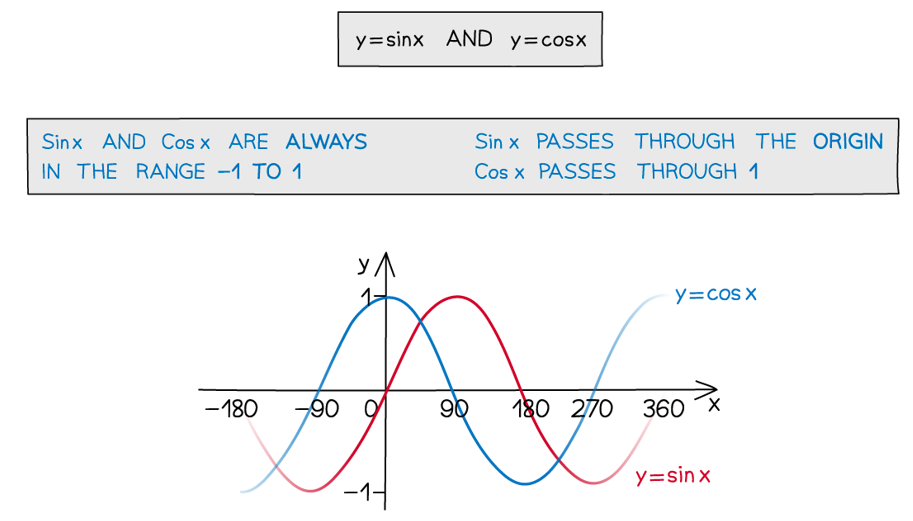
The graph of y = cos (x) has maximum displacement when x = 0
The SHM displacement equation for an object oscillating from its amplitude position (x = x0 at t = 0) is:
The displacement will be at its maximum when cos(⍵t) equals 1 or −1, when x = x0
This is because the cosine graph starts at a maximum, whereas the sine graph starts at 0
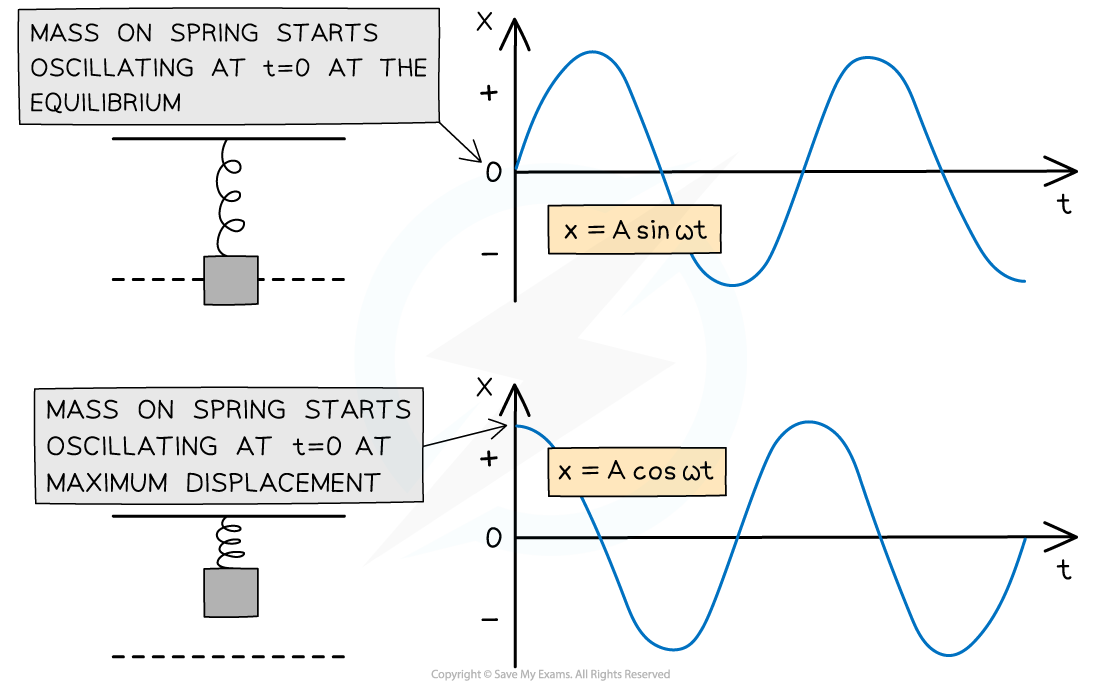
These two graphs represent the same SHM. The difference is the starting position. In these graphs, the phase difference is Φ = 0.
The Origin of the Velocity Equations in Trigonometric Form
The trigonometric equation for the velocity of an object starting from its equilibrium position (x = 0 at t = 0) is:
Where:
Φ = phase difference (radians) = 0
This comes from the fact that velocity is the rate of change of displacement
It is the differential of the relevant displacement equation from above:
The trigonometric equation for the velocity of an object starting from its amplitude position (x = x0 at t = 0) is:
This is the differential of the relevant displacement equation from above:
The Origin of the Displacement-Velocity Relation
The velocity of an object in simple harmonic motion varies as it oscillates back and forth and is given by the equation:
± = ‘plus or minus’.
The value can be negative or positive
This comes from the fact that acceleration is the rate of change of velocity
When the defining equation of simple harmonic motion is integrated using a differential equation the above equation for velocity is obtained
This equation shows that when an oscillator has a greater amplitude x0, it has to travel a greater distance in the same time and hence has greater speed v
Equations for Calculating Energy Changes in SHM
The revision note on Calculating Energy Changes in SHM explains the origin of these two equations for calculating energy changes in simple harmonic motion
Potential energy:
Total energy at the amplitude of oscillation:
Where:
m = mass (kg)
ω = angular frequency (rad s−1)
x0 = amplitude (m)
Worked Example
The graph shows the potential energy, EP, for a particle oscillating with SHM. The particle has mass 45 g.

(a) Use the graph to determine the amplitude and the period of the oscillation.
(b) Calculate the maximum speed which the particle achieves.
Answer:
(a)
Step 1: Use the graph to determine the maximum potential energy of the particle

Maximum potential energy, EPmax = 60 mJ = 60 × 10−3 J
Step 2: Determine the amplitude of the oscillation
The amplitude of the motion
is the maximum displacement
At the maximum displacement, the particle is at its highest point, hence this is the position of maximum potential energy
From the graph, when EP = 60 mJ:
= 8.0 cm2 = 8.0 × 10-4 m2
Amplitude:
Step 3: Write down the equation for the potential energy of an oscillator and rearrange for angular velocity ω
Step 4: Substitute the known values and calculate ω
Mass of the particle, m = 45 g = 45 × 10−3 kg
Step 5: Determine the time period of the oscillation
= 0.11 s
(b)
The maximum speed of the oscillator is equal to
= 57.7 × 0.028 = 1.6 m s−1
Worked Example
A student investigated the behaviour of a 200 g mass oscillating on a spring, and produced the graph shown.

(a) Determine the values for amplitude and time period
(b) Hence find the maximum kinetic energy of the oscillating mass.
Answer:
(a)
Read the values of amplitude and time period from the graph
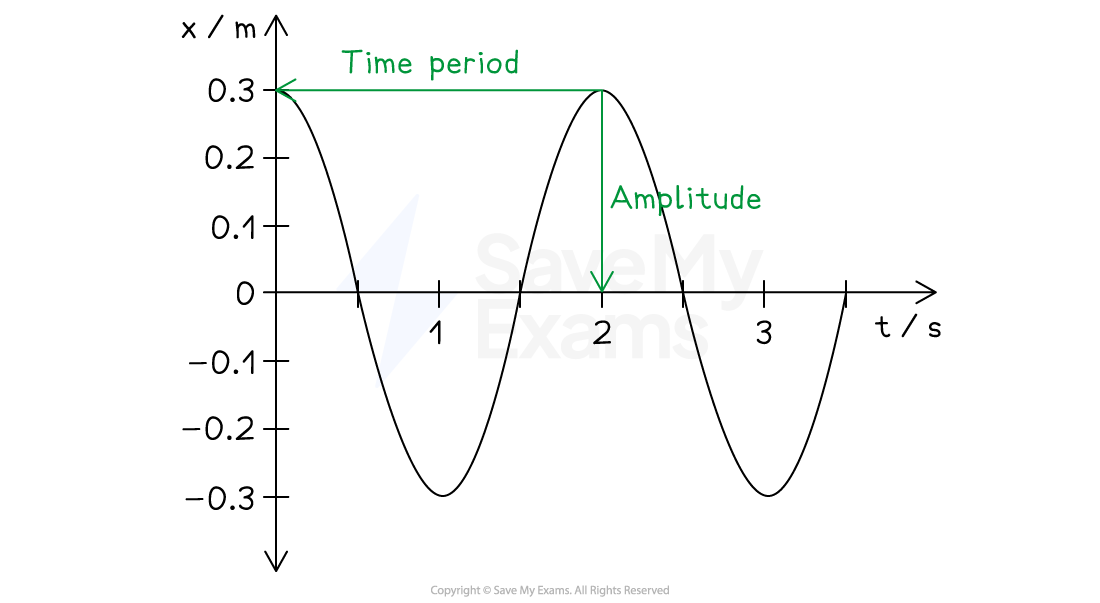
Amplitude,
= 0.3 m
Time period, T = 2.0 s
(b)
Step 1: Write down the equation for the maximum speed of an oscillator
Step 2: Write down the equation relating angular speed and time period
Step 3: Combine the two equations and calculate the maximum speed
= 0.942 m s−1
Step 4: Use the maximum speed to calculate the maximum kinetic energy of the oscillating mass
Mass of the oscillator, m = 200 g = 0.2 kg
= 0.5 × 0.2 × 0.9422 = 0.1 J
Examiner Tips and Tricks
There are a large number of equations associated with SHM. Most of them are given in the data booklet which you will be given to use in the exam
Make sure you are familiar with the equations, as you will probably need to use several different ones to solve the longer questions.

Unlock more, it's free!
Did this page help you?