Scale Diagrams (DP IB Physics) : Revision Note
Scale Diagrams
There are two methods that can be used to combine or resolve vectors
Calculation – if the vectors are perpendicular
Scale drawing – if the vectors are not perpendicular
Calculating vectors using a scale drawing involves drawings the lengths and angles of the vectors accurately using a sharp pencil, ruler and protractor
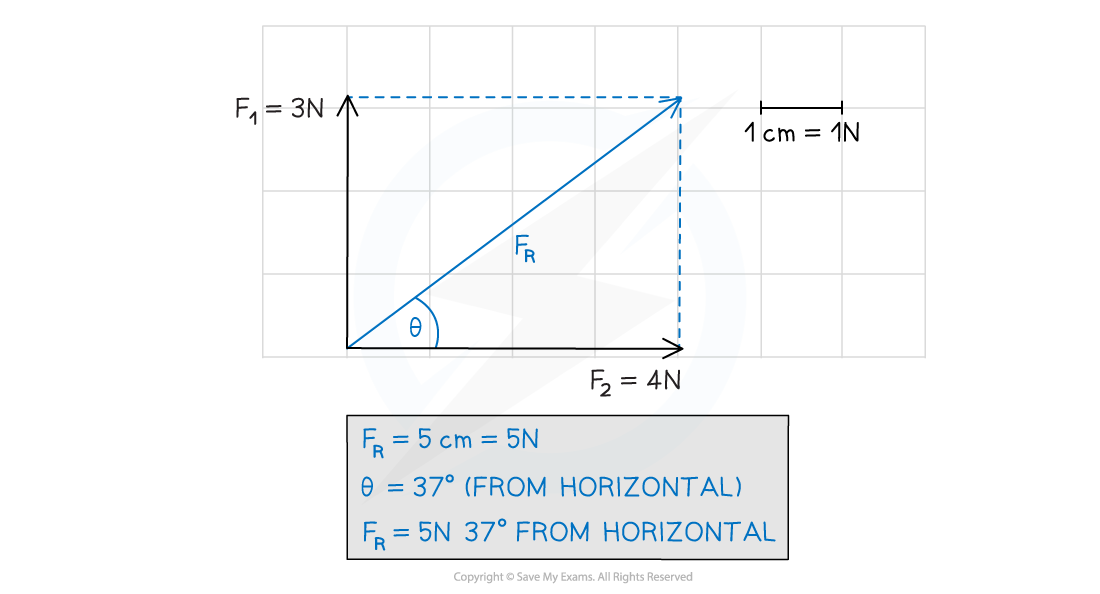
Vectors can be determined using scale diagrams
When two vectors are not at right angles, the resultant vector can be calculated using a scale drawing
Step 1: Link the vectors head-to-tail if they aren’t already
Step 2: Draw the resultant vector using the triangle or parallelogram method
Step 3: Measure the length of the resultant vector using a ruler
Step 4: Measure the angle of the resultant vector (from North if it is a bearing) using a protractor
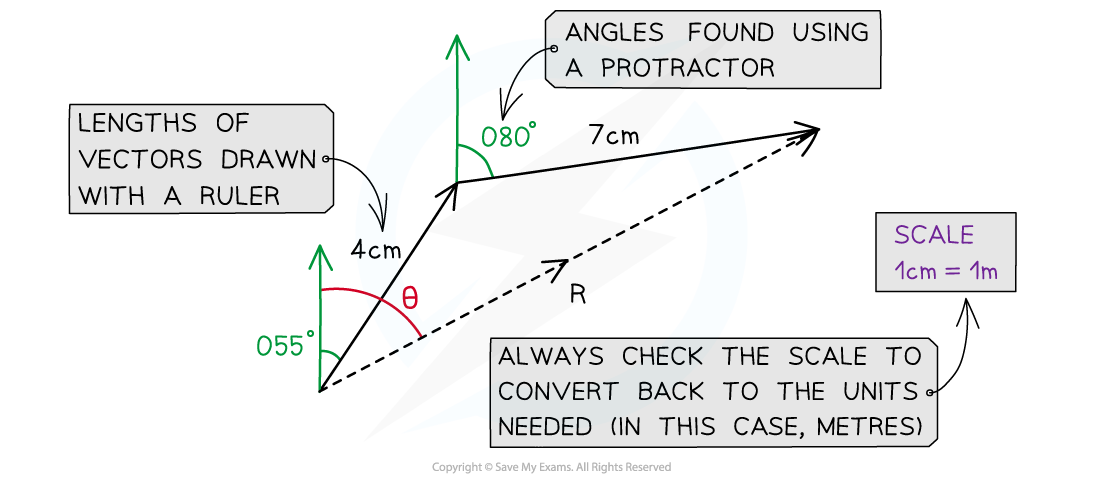
A scale drawing of two vector additions. The magnitude of resultant vector R is found using a rule and its direction is found using a protractor
Note that with scale drawings, a scale may be given for the diagram such as 1 cm = 1 km since only limited lengths can be measured using a ruler
The final answer is always converted back to the units needed in the diagram
Eg. For a scale of 1 cm = 2 km, a resultant vector with a length of 5 cm measured on your ruler is actually 10 km in the scenario
Worked Example
A hiker walks a distance of 6 km due east and 10 km due north.
By making a scale drawing of their route, find the magnitude of their displacement and its direction from the horizontal.
Answer:
Step 1: Choose a sensible scale
The distances are 6 and 10 km, so a scale of 1 cm = 1 km will fit easily on the page, but be large enough for an accurate scale drawing
Step 2: Draw the two components using a ruler and make the measurements accurate to 1 mm

Step 3: Add the resultant vector, remembering the start and finish points of the journey

Step 4: Carefully measure the length of the resultant and convert using the scale

Step 5: Measure the angle between the vector and the horizontal line

Step 6: Write the complete answer, giving both magnitude and direction
Magnitude: R = 11.7 km
Direction: θ = 59°
Examiner Tips and Tricks
It should be noted that some of the examples used on this page demonstrate the use of scale diagrams where the vectors are placed at right angles - it would be quicker to determine the resultant force of these via calculation as simple trigonometry can be used
Scale diagram questions will typically involve vector triangles that do not contain a right angle

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
