First Law of Thermodynamics (DP IB Physics): Revision Note

The First Law of Thermodynamics

• The first law of thermodynamics is based on the principle of conservation of energy

• When energy is put into a gas by heating it or doing work on it, its internal energy must increase:

energy supplied by heating = change in internal energy + work done on the system

• The first law of thermodynamics is therefore defined as:

• Where:

  • Q = energy supplied to the system by heating (J)

  • ΔU = change in internal energy (J)

  • W = work done by the system (J)

• The first law of thermodynamics applies to all situations, not just to gases

  • There is an important sign convention used for this equation

• A positive value for internal energy (+ΔU) means:

  • The internal energy ΔU increases

  • Heat Q is added to the system (+Q)

  • Work W is done on the system (–W)

• A negative value for internal energy (−ΔU) means:

  • The internal energy ΔU decreases

  • Heat Q is taken away from the system (–Q)

  • Work W is done by the system (+W)

Graphs of Constant Pressure & Volume

• Graphs of pressure p against volume V can provide information about the work done and internal energy of the gas

  • The work done is represented by the area under the line

• A constant pressure process is represented as a horizontal line

  • If the volume is increasing (expansion), work is done by the gas (on the surroundings) and internal energy decreases (ΔU = q − W)

  • If the arrow is reversed and the volume is decreasing (compression), work is done on the gas and internal energy increases (ΔU = q + W)

  • The volume of the gas is made smaller, so more collisions between the molecules of the gas and the walls of the container occur. This creates a higher pressure. 

• A constant volume process is represented as a vertical line

  • In a process with constant volume, the area under the curve is zero

  • Therefore, no work is done when the volume stays the same

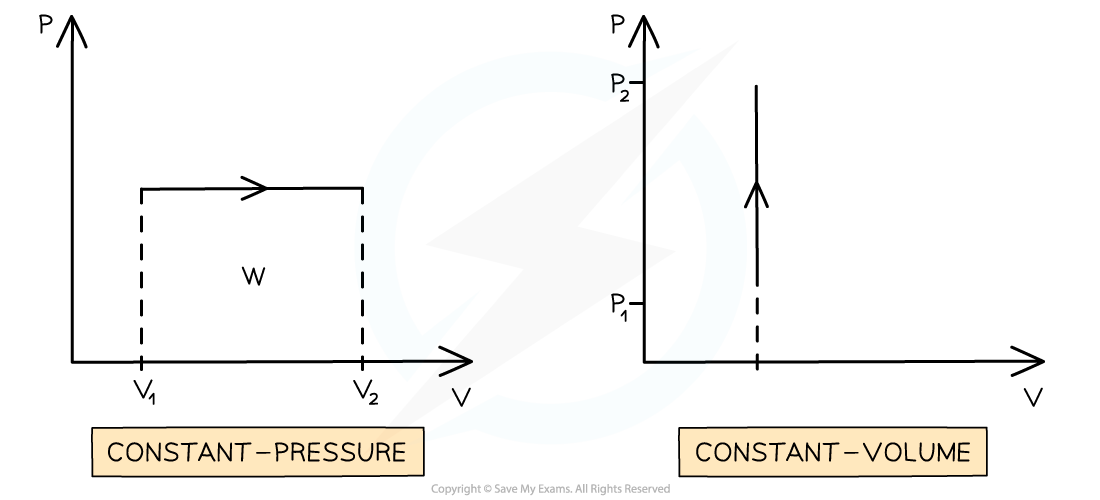
Work is only done when the volume of a gas changes