Gas Pressure (DP IB Physics) : Revision Note
Calculating Gas Pressure
Pressure is defined as
The force applied per unit area
For example, when a drawing pin is pushed downwards:
It is pushed into the surface, rather than up towards the finger
This is because the sharp point is more concentrated (a small area) creating a larger pressure
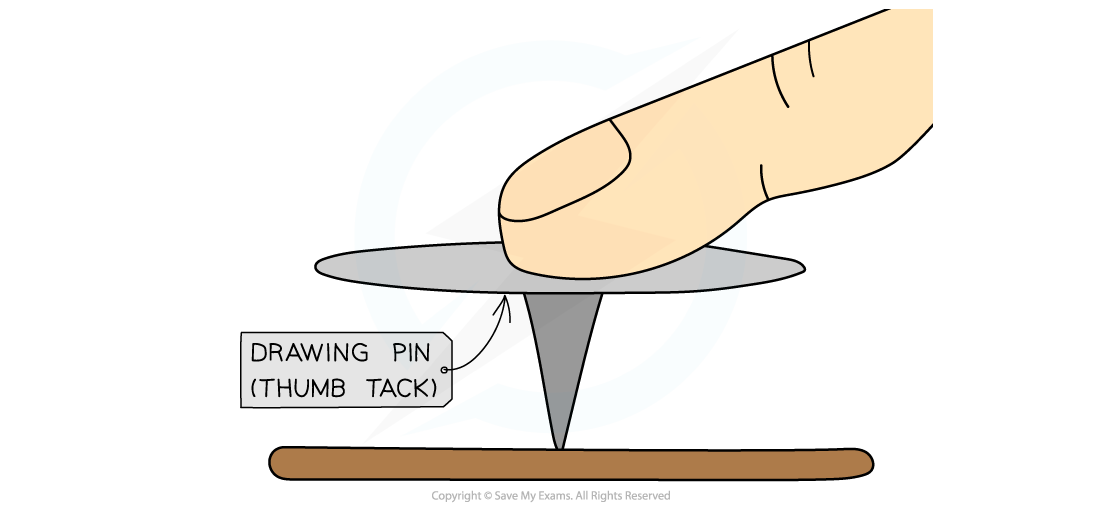
When you push a drawing pin, it goes into the surface (rather than your finger)
When an object is immersed in a liquid, the liquid will exert pressure, squeezing the object
The pressure exerted on objects in fluids creates forces against surfaces
These forces act at 90 degrees (at right angles) to the surface
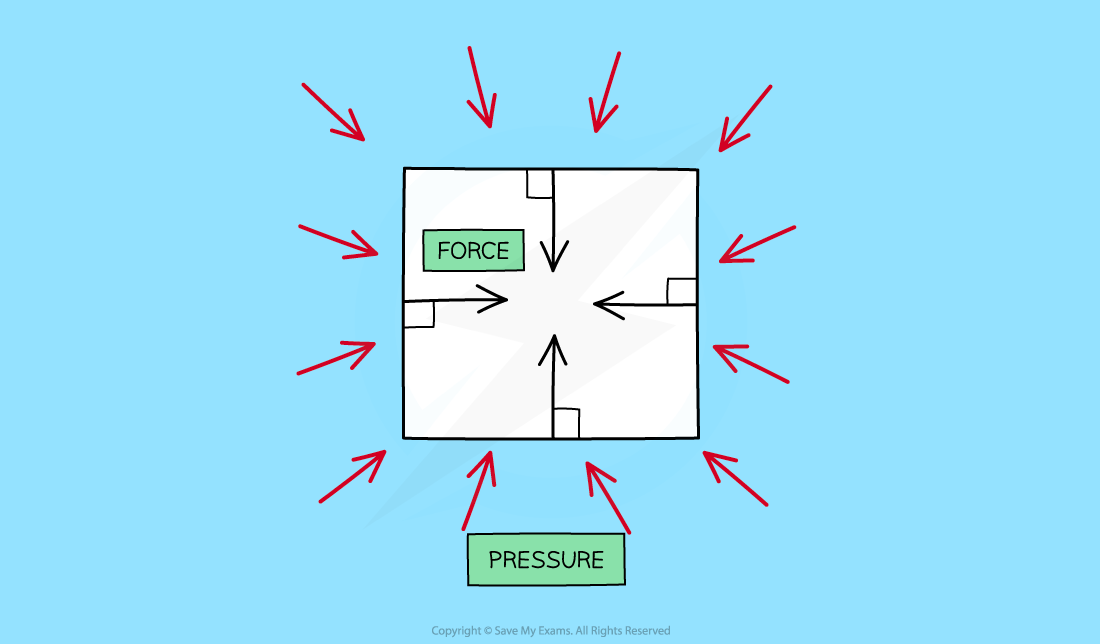
The pressure of a fluid on an object creates a force normal (at right angles) to the surface
The equation for pressure is:
Where:
P = pressure (Pa)
F = force (N)
A = cross-sectional area (m2)
Pressure is measured in Pascals (Pa)
This equation is only relevant when gas molecules exert a force perpendicular to the surface

Gas molecules bouncing off the walls of a container
It is possible for someone to experience this force by closing their mouth and forcing air into their cheeks
The strain on the cheeks is due to the force of the gas particles pushing at right angles to the cheeks
This equation means:
If a force is spread over a large area it will result in a small pressure
If it is spread over a small area it will result in a large pressure
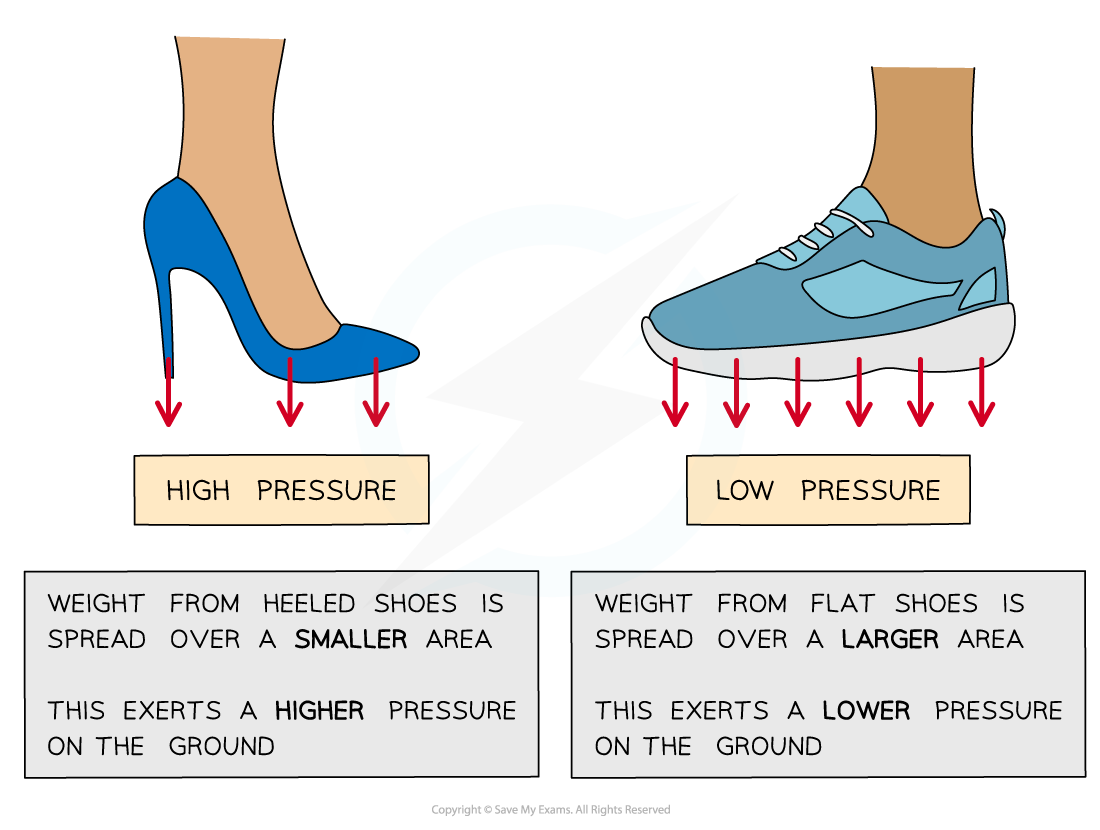
High heels produce a higher pressure on the ground because of their smaller area, compared to flat shoes
Worked Example
The diagram below shows the parts of the lifting machine used to move a platform of cross-sectional area 2.73 × 10-2 m2 up and down.
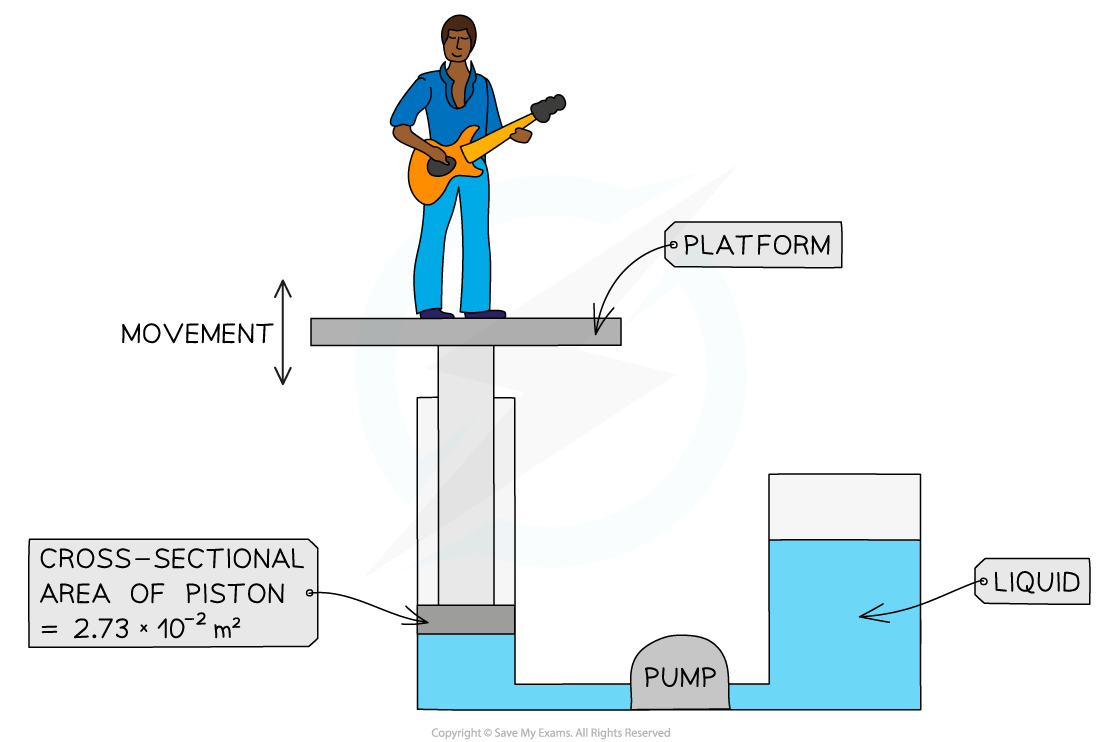
The pump creates pressure in the liquid of 5.28 × 105 Pa to move the platform upwards.
Calculate the force that the liquid applies to the piston.
Answer:
Step 1: List the known quantities
Cross-sectional area, A = 2.73 × 10-2 m2
Pressure, P = 5.28 × 105 Pa
Step 2: Write down the relevant equation

Step 3: Rearrange for the force, F
F = p × A
Step 4: Substitute the values into the equation
F = (5.28 × 105) × (2.73 × 10-2) = 14 414.4
Step 5: Round to the appropriate number of significant figures and quote the correct unit
F = 14 400 N = 14.4 kN (3 s.f)
Examiner Tips and Tricks
Make sure A is always the cross-sectional area of the surface that the force is being applied upon, especially if there are multiple areas given in the question.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
