Conservation of Mechanical Energy (DP IB Physics): Revision Note
Mechanical Energy
Mechanical energy is the sum of kinetic energy, gravitational potential energy and elastic potential energy
Mechanical energy =
An example of a system that has mechanical energy is a spring and mass system
The change in the total mechanical energy of a system should be interpreted in terms of the work done on the system by any non-conservative force
A non-conservative force is one that dissipates energy away from the system, such as friction
When a vertical spring is extended and contracted, its energy is converted into other forms
Although the total energy of the spring will remain constant, it will have changing amounts of:
Elastic potential energy (EH or EPE)
Kinetic energy (Ek or KPE)
Gravitational potential energy (Ep or GPE)
When a vertical mass is hanging on a spring and it moves up and down, its energy will convert between the three in various amounts
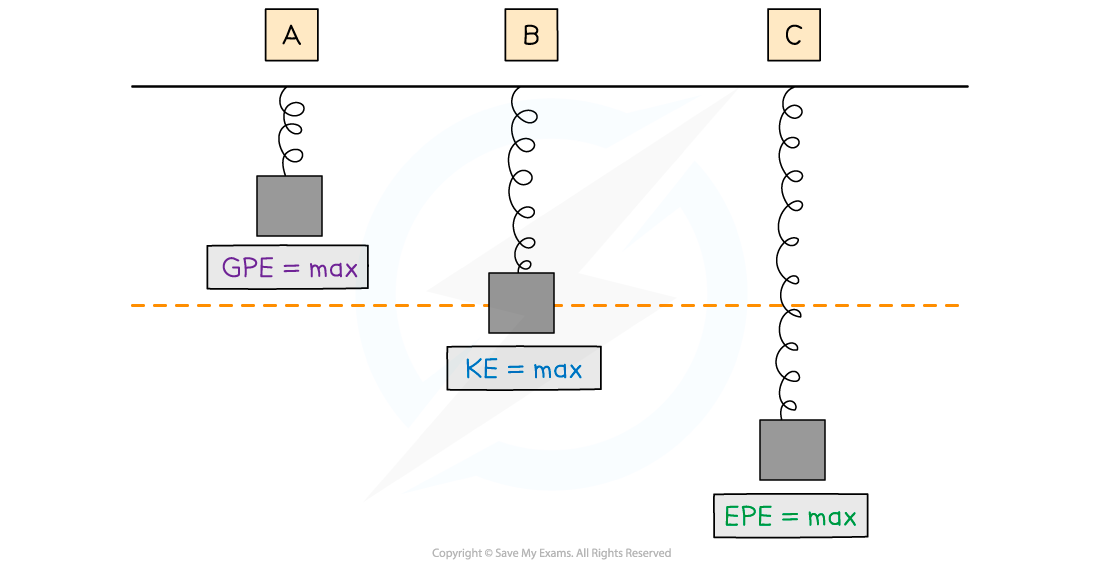
Position | GPE | KE | EPE |
A | Maximum | Zero | Some |
B | Some | Maximum | Some |
C | Minimum | Zero | Maximum |
For a horizontal mass on a spring system, there is no gravitational potential energy to consider because this is constant
The spring would only convert between kinetic and elastic potential energy
Conservation of Mechanical Energy
In the absence of frictional, resistive forces, the total mechanical energy of a system is conserved
This means the total kinetic, gravitational potential and elastic potential energy is the same throughout the motion of the system
Because the total energy of a system is always conserved
There are many scenarios that involve the transfer of kinetic energy into gravitational potential, or vice versa
Some examples are:
a swinging pendulum
objects in freefall
sports that involve falling, such as skiing and skydiving
Using the principle of conservation of energy, and taking any drag forces as negligible:
Loss in gravitational potential energy = Gain in kinetic energy
Another example is if a ball on a spring oscillates horizontally
In this case:
Loss in elastic potential energy = Gain in kinetic energy
The change in energy is the work done on the system. The types of changes depend on the system
Worked Example
The diagram below shows a skier on a slope descending 750 m at an angle of 25° to the horizontal.
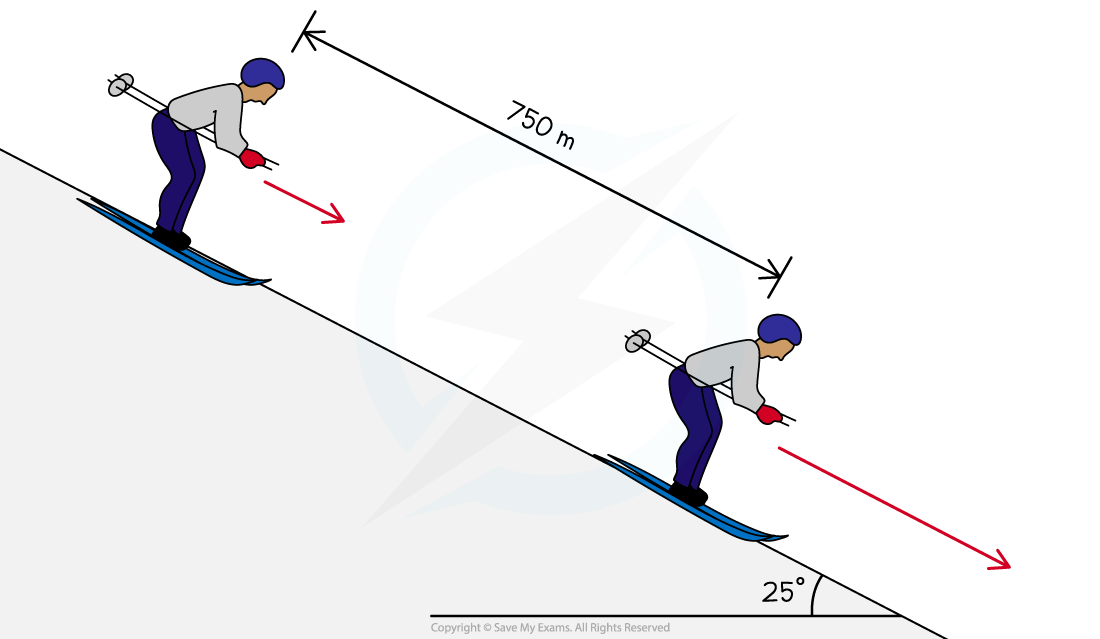
Calculate the final speed of the skier, assuming that he starts from rest and 15% of his initial gravitational potential energy is not transferred to kinetic energy.
Answer:
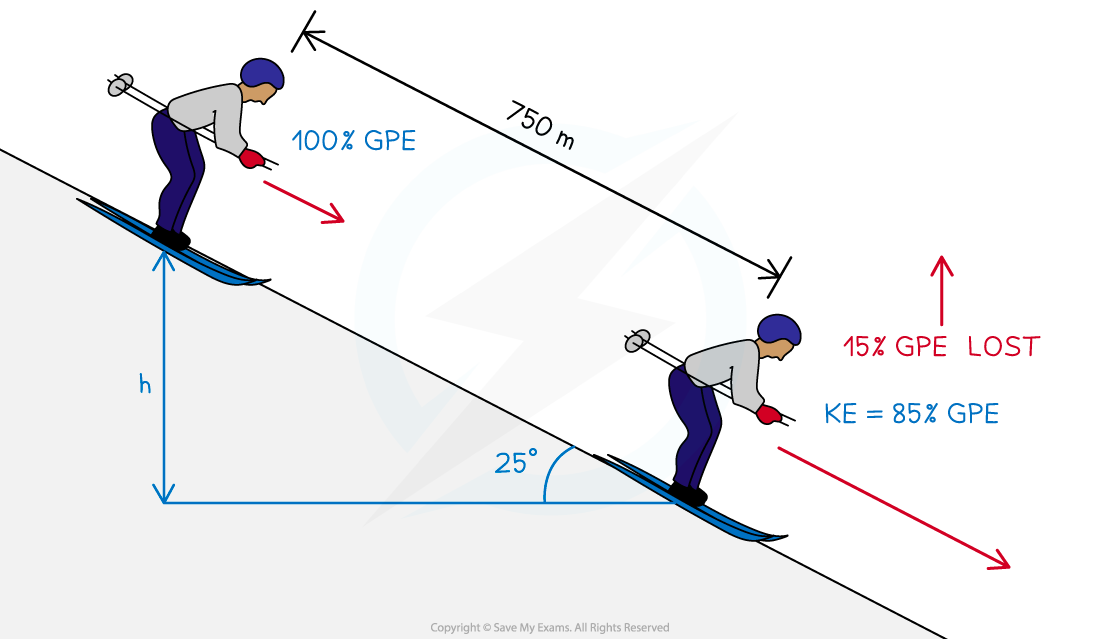
Step 1: Write down the known quantities
Vertical height, h = 750 sin 25°
Ek = 0.85 Ep
Step 2: Equate the equations for Ek and Ep
Ek = 0.85 Ep
½ mv2 = 0.85 × mgh
Step 3: Rearrange for final speed, v
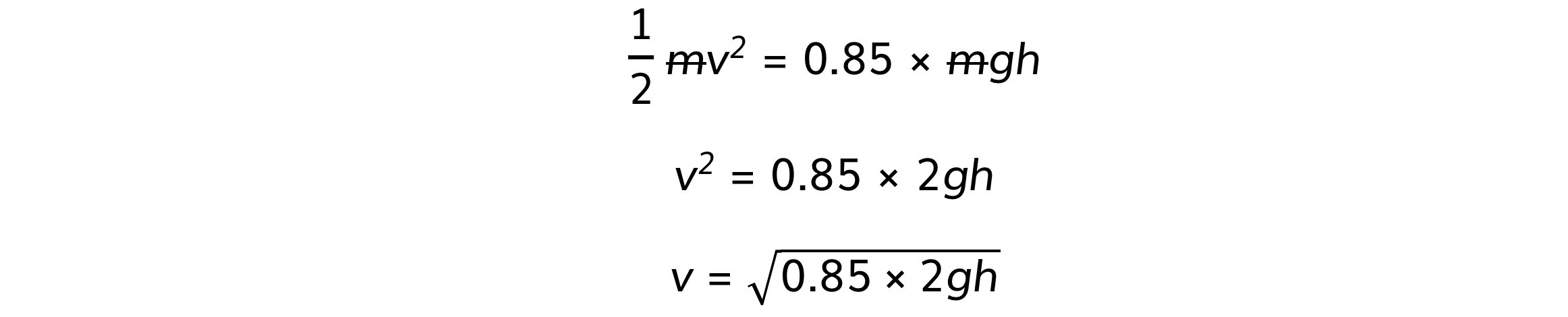
Step 4: Calculate the final speed, v

Examiner Tips and Tricks
Exam questions often ask about the 'work done' in the process. This means how much energy is transferred. You must consider all the energy changes in the system and remember that mechanical energy is always conserved. This is essentially the conservation of energy.

Unlock more, it's free!
Did this page help you?