Revision NotesExam QuestionsFlashcardsPast Papers
IBPhysicsDPHLRevision NotesSpace, Time & MotionRigid Body MechanicsRotational Kinetic Energy

Rotational Kinetic Energy (DP IB Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Rotational Kinetic Energy

  • A body moving with linear velocity has an associated linear kinetic energy given by

E subscript k space equals space 1 half m v squared

E subscript k space equals space fraction numerator p squared over denominator 2 m end fraction

  • Similarly, a rotating body with angular velocity has an associated rotational kinetic energy given by

E subscript k space equals space 1 half I omega squared

E subscript k space equals space fraction numerator L squared over denominator 2 I end fraction

  • Where:

    • E subscript k = rotational kinetic energy (J)

    • I = moment of inertia (kg m2)

    • omega = angular velocity (rad s−1)

    • L = angular momentum (kg m2 s−1)

Rolling without slipping

  • Circular objects, such as wheels, are made to move with both linear and rotational motion

    • For example, the wheels of a car, or bicycle rotate causing it to move forward

  • Rolling motion without slipping is a combination of rotating and sliding (translational) motion

  • When a disc rotates:

    • Each point on the disc has a different linear velocity depending on its distance from the centre open parentheses v space proportional to space r close parentheses

    • The linear velocity is the same at all points on the circumference 

  • When a disc slips, or slides:

    • There is not enough friction present to allow the object to roll

    • Each point on the object has the same linear velocity

    • The angular velocity is zero

  • So, when a disc rolls without slipping:

    • There is enough friction present to initiate rotational motion allowing the object to roll

    • The point in contact with the surface has a velocity of zero

    • The centre of mass has a velocity of v space equals space omega r

    • The top point has a velocity of 2 v or 2 omega r

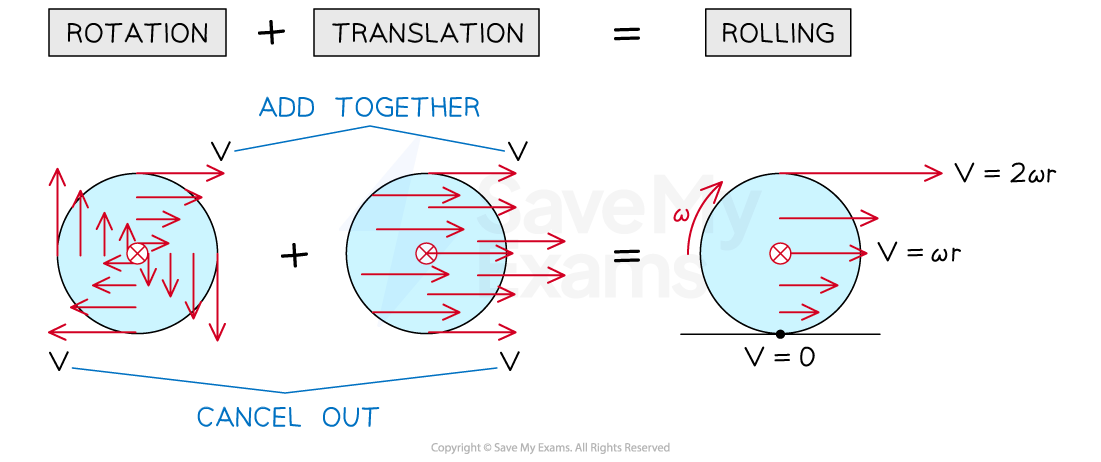
E16CHGH6_1-4-9-rotational-kinetic-energy-rolling-without-slipping

Rolling motion is a combination of rotational and translational motion. The resultant velocity at the bottom is zero and the resultant velocity at the top is 2v

Rolling down a slope

  • Another common scenario involving rotational and translational motion is an object (usually a ball or a disc) rolling down a slope

  • At the top of the slope, a stationary object will have gravitational potential energy equal to

E subscript p space equals space m g increment h

  • As the object rolls down the slope, the gravitational potential energy will be transferred to both translational (linear) and rotational kinetic energy

  • At the bottom of the slope, the total kinetic energy of the object will be equal to

E subscript K space t o t a l end subscript space equals space 1 half m v squared space plus space 1 half I omega squared

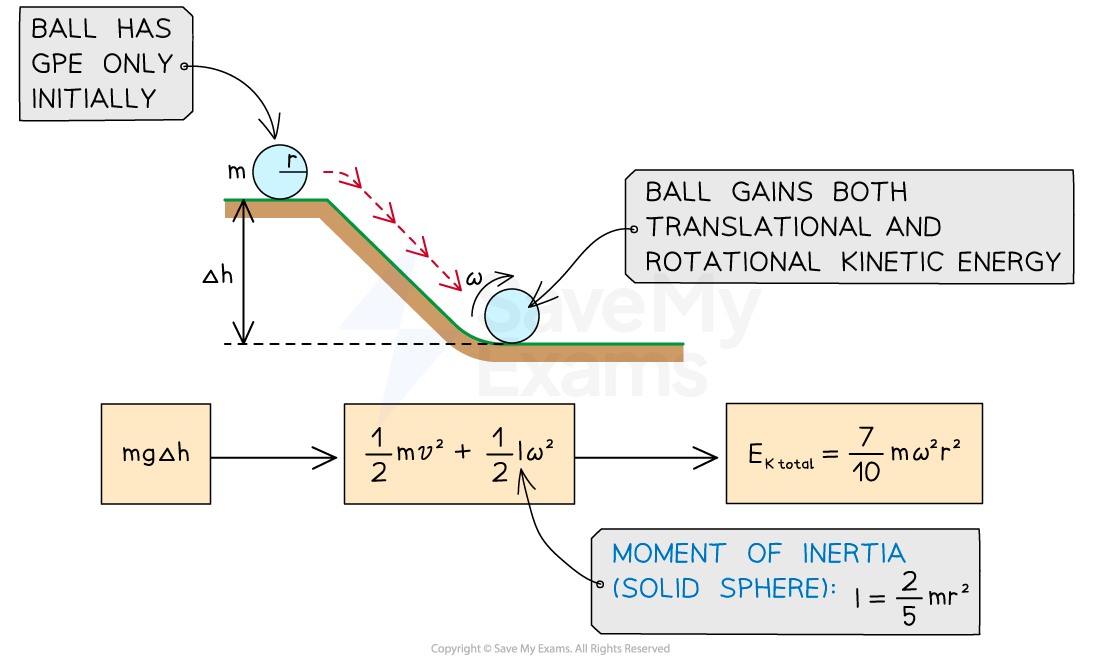
1-4-9-rotational-kinetic-energy-rolling-down-a-slope-ib-2025-physics

  • The linear or angular velocity can then be determined by

    • Equating E subscript p and E subscript K space t o t a l end subscript

    • Using the equation for the moment of inertia of the object

    • Using the relationship between linear and angular velocity v space equals space omega r

  • For example, for a ball (a solid sphere) of mass m and radius r, its moment of inertia is

I space equals space 2 over 5 m r squared

  • Equating the equations for E subscript p and E subscript K space t o t a l end subscript and simplifying gives

m g increment h space equals space 1 half m open parentheses omega r close parentheses squared space plus space 1 half open parentheses 2 over 5 m r squared close parentheses omega squared

m g increment h space equals space 1 half m omega squared r squared space plus space 1 fifth m omega squared r squared

m g increment h space equals space 7 over 10 m omega squared r squared

Worked Example

A flywheel of mass M and radius R rotates at a constant angular velocity ω about an axis through its centre. The rotational kinetic energy of the flywheel is E subscript K.

The moment of inertia of the flywheel is 1 half M R squared.

A second flywheel of mass 1 half M and radius 1 half R is placed on top of the first flywheel. The new angular velocity of the combined flywheels is 2 over 3 omega.

1-4-9-rotational-kinetic-energy-flywheel-mcq-worked-example-ib-2025-physics

What is the new rotational kinetic energy of the combined flywheels?

A. E subscript K over 2          

B.  E subscript K over 4          

C. E subscript K over 8           

D. E subscript K over 24

Answer:  A

  • The kinetic energy of the first flywheel is

E subscript K space equals space 1 half I omega squared space equals space 1 half cross times open parentheses 1 half M R squared close parentheses cross times omega squared

E subscript K space equals space 1 fourth M R squared omega squared

  • The combined flywheels have a total moment of inertia of

I subscript n e w end subscript space equals space I subscript 1 space plus space I subscript 2

I subscript n e w end subscript space equals space 1 half M R squared space plus space 1 half open parentheses 1 half M close parentheses open parentheses 1 half R close parentheses squared

I subscript n e w end subscript space equals space 9 over 16 M R squared

  • The kinetic energy of the combined flywheels is

E subscript K space n e w end subscript space equals space 1 half I subscript n e w end subscript omega subscript n e w end subscript squared space equals space 1 half cross times open parentheses 9 over 16 M R squared close parentheses cross times open parentheses 2 over 3 omega close parentheses squared

E subscript K space n e w end subscript space equals space 1 half cross times open parentheses 1 fourth M R squared omega squared close parentheses space equals space 1 half E subscript K

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Angular ImpulseNext:Reference Frames
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.