Rotational Equilibrium (DP IB Physics) : Revision Note
Rotational Equilibrium
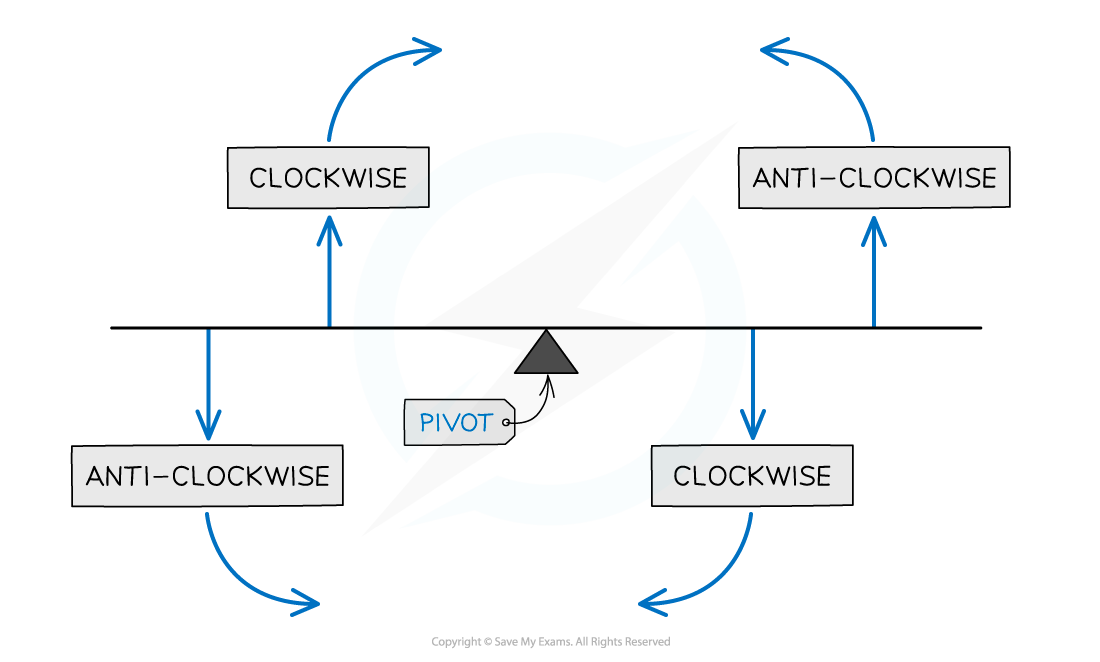
If the resultant torque acting on a body is zero, it is said to be in rotational equilibrium
A body in rotational equilibrium will therefore remain at rest, or rotate with a constant angular velocity
This is analogous to Newton's First Law for translational equilibrium
This means a body is in rotational equilibrium if:
The sum of the clockwise torques is equal to the sum of the anticlockwise torques
This is known as the principle of torques (also called the principle of moments)
It can be applied to a range of scenarios, such as a balanced beam
A beam is an example of a rigid, extended body
A beam in rotational equilibrium

When the forces on a beam are balanced on each side of a pivot, the resultant torque on the beam is zero, so it will be in rotational equilibrium
Worked Example
Four beams of the same length each have three forces acting on them.
Which of the beams is in rotational equilibrium?

Answer: C
A beam is in rotational equilibrium when there is zero resultant torque acting on it
In rotational equilibrium:
Total clockwise torque = Total anticlockwise torque
Consider beam C, taking torques from the centre of the beam (where its weight acts) :
Torque, (as
)
Total clockwise torque = 15 × 50 = 750 N cm
Total anticlockwise torque = 25 × 30 = 750 N cm
The total clockwise torque (750 N cm) = total anticlockwise torque (750 N cm), therefore, beam C is in rotational equilibrium
The other beams are not in rotational equilibrium because...
Beam A has a resultant torque of 310 N cm anticlockwise
Beam B has a resultant torque of 370 N cm clockwise
Beam D has a resultant torque of 1790 N cm clockwise
Examiner Tips and Tricks
When considering an object in rotational equilibrium, choosing certain points can simplify calculations of resultant torque. Remember, you can choose any point, not just the axis of rotation.
To simplify your calculation, choose a point where the torque of (most of) the forces are unknown, or when you need to determine where the resultant torque is zero. To do this, choose a point through which the lines of action of the forces pass
Unbalanced Torque
A resultant torque causes angular acceleration
This is analogous to the way a resultant force causes linear acceleration
The direction of the angular acceleration depends on the direction of the net resultant torque
A beam with an unbalanced torque

If there is a net resultant torque in the clockwise or anti-clockwise direction, the beam will also have an angular acceleration in that direction
Worked Example
A uniform plank of mass 30 kg and length 10 m is supported at its left end and at a point 1.5 m from the centre.

Calculate the maximum distance r to which a boy of mass 50 kg can walk without tipping the rod over.
Answer:
Step 1: Analyse the scenario and identify the forces
Let the forces at each support be FL (reaction force from the left support) and FR (reaction force from the right support)
These are vertically upwards
Just before the plank tips over, the system is in rotational equilibrium
When the plank begins to tip over, the left support force FL will become zero since the rod will no longer touch the support

Step 2: Take torques about the right support
Torque = Fr sin θ (θ = 90° for all)
Clockwise torque = 50 × g × r
Anti-clockwise torque = 30 × g × 1.5
Step 3: Equate the clockwise and anti-clockwise torques
r = 0.90 m
Therefore, the plank will begin to tip once the boy is 0.90 m from the right support
Worked Example
The diagram shows three forces acting on a wheel.

Determine the net resultant torque about the axis of rotation O. State whether the angular acceleration that is produced is clockwise or anticlockwise.
Answer:
Step 1: Recall the equation for torque
Step 2: Find the sum of the torques in the clockwise direction
Torque of the 10 N force:
Torque of the 9 N force:
Total clockwise torque = 2.5 + 2.25 = 4.75 N m
Step 3: Calculate the torque in the anti-clockwise direction

Torque of the 12 N force:
Total anti-clockwise torque = 0.6 N m
Step 4: Determine the net resultant torque
Resultant torque = sum of clockwise torques − sum of anti-clockwise torques
Resultant torque:
= 4.75 − 0.6 = 4.15 N m, clockwise
Direction of angular acceleration: clockwise
Examiner Tips and Tricks
You should know that torque is a vector quantity, however, at this level, you will only need to consider whether it produces clockwise or anti-clockwise motion

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
