Rutherford Scattering & Nuclear Radius (DP IB Physics)

Nuclear Radius

• The radius of a nucleus depends on the nucleon number A of the atom

  • The greater the number of nucleons a nucleus has, the greater the space the nucleus occupies, hence giving it a larger radius

• The exact relationship between the radius and nucleon number can be determined from experimental data, such as Rutherford scattering

• By doing this, physicists were able to deduce the following relationship:

• Where:

  • R = nuclear radius (m)

  • A = nucleon / mass number

  • R₀ = Fermi radius

• The constant of proportionality R₀ = 1.20 × 10⁻¹⁵ m is known as the Fermi radius

• This is the radius of a hydrogen nucleus which contains only one proton (A = 1)

Nuclear Density

• Assuming that the nucleus is spherical, its volume is equal to:

• Combining this with the expression for nuclear radius gives:

• This tells us that the nuclear volume V is proportional to the mass of the nucleus m, which is equal to

• Where u = atomic mass unit (kg)

• Using the definition for density, nuclear density is equal to:

• Since the mass number A cancels out, the remaining quantities in the equation are all constants

• Therefore, this shows the density of the nucleus is:

  • The same for all nuclei

  • Independent of the radius

• The fact that nuclear density is constant shows that nucleons are evenly separated throughout the nucleus regardless of their size

• The accuracy of nuclear density depends on the accuracy of the constant R₀

  • As a guide, nuclear density should always be of the order 10¹⁷ kg m^–3

• Nuclear density is significantly larger than atomic density which suggests:

  • The majority of the atom’s mass is contained in the nucleus

  • The nucleus is very small compared to the atom

  • Atoms must be predominantly empty space

Rutherford Scattering Experiment

• In the Rutherford scattering experiment, alpha particles are fired at a thin gold foil

• Initially, before interacting with the foil, the particles have kinetic energy equal to

• Some of the alpha particles are found to come straight back from the gold foil

• This indicates that there is electrostatic repulsion between the alpha particles and the gold nucleus

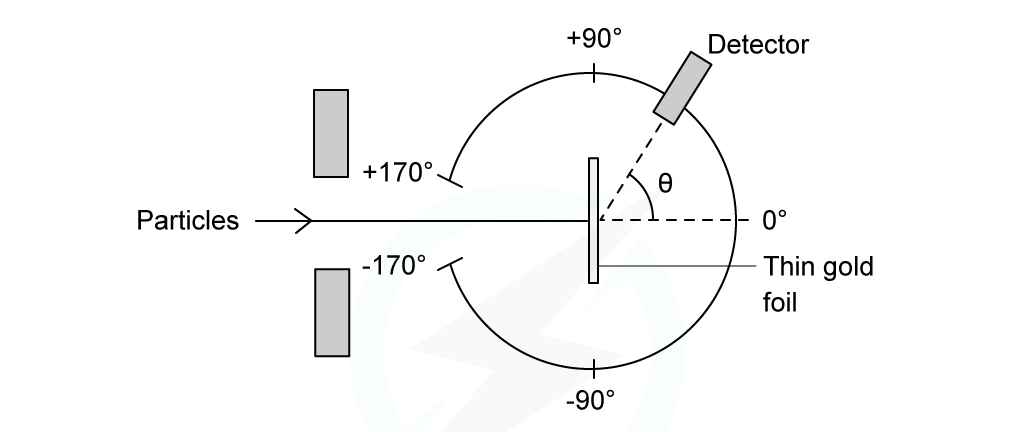
Experimental set-up of the Rutherford alpha scattering experiment

• At the point of closest approach d, the repulsive force reduces the speed of the alpha particles to zero momentarily, before any change in direction

• At this point, the initial kinetic energy of the alpha particle is equal to the electric potential energy  of the target nucleus:  

• Where the electric potential energy is given by

• Where:

  • Charge of an alpha particle, Q = 2e

  • Charge of a target nucleus, q = Ze

  • Z = proton (atomic) number

  • e = elementary charge (C)

  • k = Coulomb constant

• This gives an expression for the potential energy at the point of repulsion:

• Which, due to the conservation of energy also gives the initial kinetic energy possessed by the alpha particle

• Rearranging for the distance of closest approach d

• This gives a value for the radius of the nucleus, assuming the alpha particle is fired at a high energy

The closest approach method of determining the size of a gold nucleus