Photon Energy (DP IB Physics) : Revision Note
Photons & Atomic Transitions
The Photon Model
Photons are fundamental particles that make up all forms of electromagnetic radiation
A photon is defined as
A massless “packet” or a “quantum” of electromagnetic energy
This means that the energy transferred by a photon is not continuous but as discrete packets of energy
In other words, each photon carries a specific amount of energy and transfers this energy all in one go
This is in contrast to waves which transfer energy continuously
Atomic Energy Levels
Electrons in an atom occupy certain energy states called energy levels
Electrons will occupy the lowest possible energy level as this is the most stable configuration for the atom
When an electron absorbs or emits a photon, it can move between these energy levels, or be removed from the atom completely
Excitation
When an electron moves to a higher energy level, the atom is said to be in an excited state
To excite an electron to a higher energy level, it must absorb a photon
Electrons can also move back down to a lower energy level by de-excitation
To de-excite an electron to a lower energy level, it must emit a photon
Ionisation
When an electron is removed from an atom, the atom becomes ionised
An electron can be removed from any energy level it occupies
However, the ionisation energy of an atom is the minimum energy required to remove an electron from the ground state of an atom
Representing Energy Levels
Energy levels can be represented as a series of horizontal lines
The line at the bottom with the greatest negative energy represents the ground state
The lines above the ground state with decreasing energies represent excited states
The line at the top, usually 0 V or infinity
, represents the ionisation energy
Energy Levels in a Hydrogen Atom
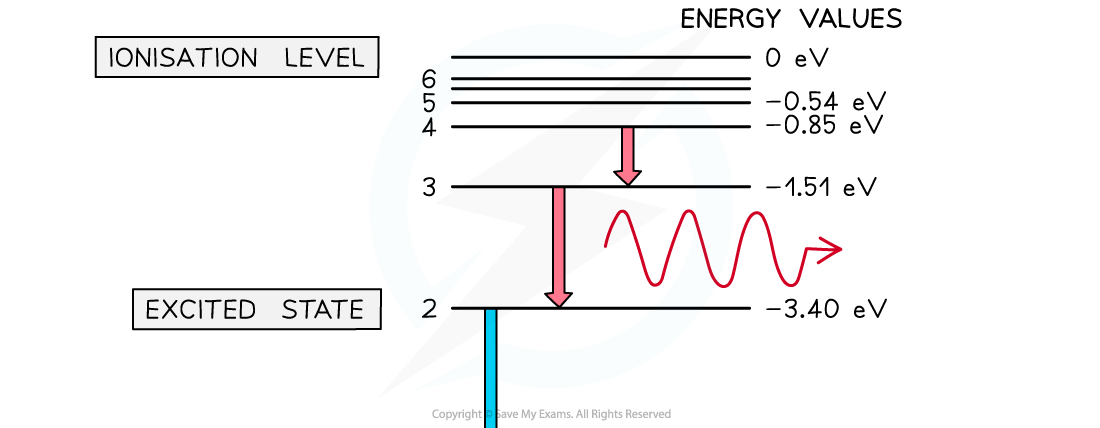

A photon is emitted when an electron moves from a higher energy state to a lower energy state. The energy of the emitted photon is equal to the difference in energy between the energy levels in the transition.
Worked Example
Explain how atomic spectra provide evidence for the quantisation of energy in atoms.
Answer:
Step 1: Outline the meaning of atomic spectra
Atomic spectra show the spectrum of discrete wavelengths emitted or absorbed by a specific atom
Step 2: Describe the relationship between energy and wavelength
Photon energy is related to frequency and wavelength
Therefore, photons with discrete wavelengths have discrete energies equal to the difference between two energy levels
Step 3: Explain how atomic spectra give evidence for the quantisation of energy
Photons arise from electron transitions between energy levels
This happens when an electron is excited, or de-excited, from one energy level to another, by either emitting or absorbing light of a specific wavelength
Since atomic spectra are made up of discrete wavelengths, this shows that atoms must contain discrete, or quantised, energy levels
Worked Example
The diagram shows the electron energy levels in an atom of hydrogen.

Determine the number of possible wavelengths that can be produced from transitions between the n = 4 excited state and the n = 1 ground state.
Answer:
There are six possible wavelengths that could be produced from the different energy level transitions
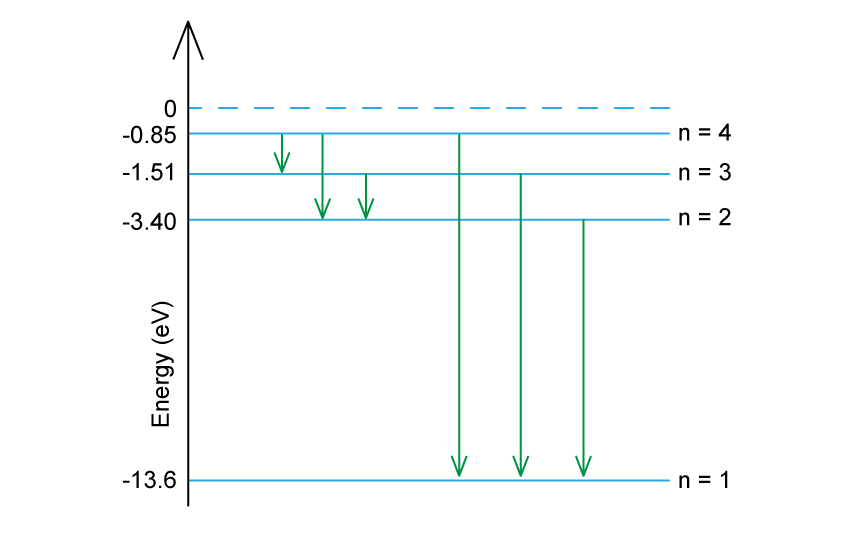
The possible transitions are:
n = 4 to n = 3
n = 4 to n = 2
n = 4 to n = 1
n = 3 to n = 2
n = 3 to n = 1
n = 2 to n = 1
Examiner Tips and Tricks
Make sure you learn the definition for a photon: discrete quantity / packet / quantum of electromagnetic energy are all acceptable definitions
Calculating Photon Energy
Each line of the emission spectrum corresponds to a different energy level transition within the atom
Electrons can transition between energy levels absorbing or emitting a discrete amount of energy
An excited electron can transition down to the next energy level or move to a further level closer to the ground state
For example, if an atom has six energy levels:
At low temperatures, most electrons will occupy the ground state n = 1
At high temperatures, electrons may be excited to the most excited state n = 6

Energy and frequency of a photon are directly proportional
The energy of a photon can be calculated using the formula:
Using the wave equation, energy can also be equal to:
Where:
E = energy of the photon (J)
h = Planck's constant (J s)
c = the speed of light (m s−1)
f = frequency (Hz)
λ = wavelength (m)
This equation tells us:
The higher the frequency of EM radiation, the higher the energy of the photon
The energy of a photon is inversely proportional to the wavelength
A long-wavelength photon of light has a lower energy than a shorter-wavelength photon
Difference in discrete energy levels
The difference between two energy levels is equal to a specific photon energy
The energy of the photon is given by:
Where:
E1 = energy of the lower level (J)
E2 = energy of the higher level (J)
Using the wave equation, the wavelength of the emitted, or absorbed, radiation can be related to the energy difference by the equation:
This equation shows that:
The larger the difference in energy between two levels ΔE, the shorter the wavelength λ and vice versa
Worked Example
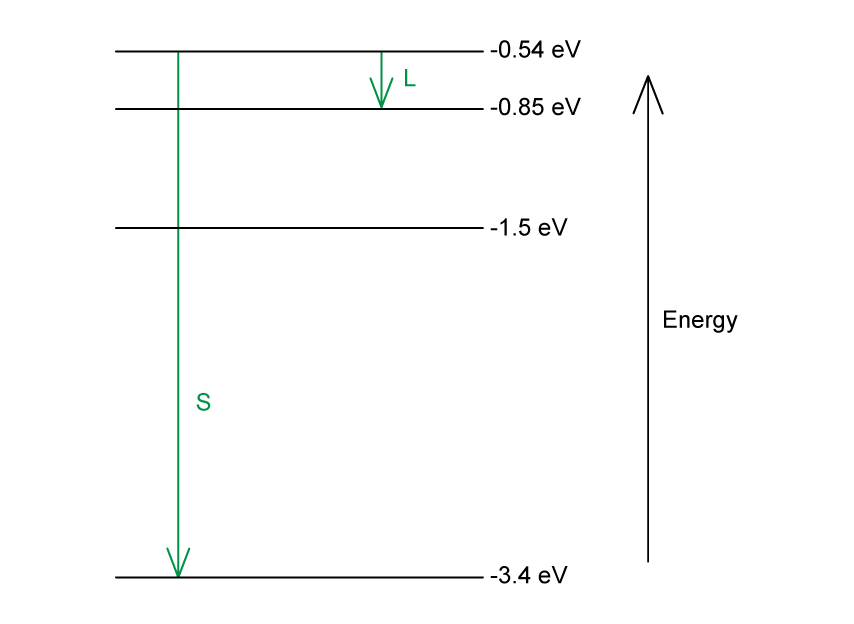
Some electron energy levels in atomic hydrogen are shown below.

The longest wavelength produced as a result of electron transitions between two of the energy levels is 4.0 × 10–6 m.
(a) Draw an arrow to show the transition that would produce:
A photon of wavelength 4.0 × 10–6 m. Mark with the letter L.
The photon with the shortest wavelength. Mark with the letter S.
(b) Calculate the wavelength for the transition giving rise to the shortest wavelength.
Answer:
(a)
Photon energy and wavelength are inversely proportional
Therefore, the largest energy change corresponds to the shortest wavelength (line S)
The smallest energy change corresponds to the longest wavelength (line L)
(b)
Step 1: Write down the equation linking wavelength and energy
Step 2: Identify the energy levels that give rise to the shortest wavelength
The shortest wavelength photon will come from a transition between the energy levels that have the largest difference:
Therefore, the greatest possible difference in energy is
Step 3: Calculate the wavelength
To convert from eV to J: multiply by 1.6 × 10−19 J
= 4.347 × 10−7 m = 435 nm
Worked Example
Light of wavelength 490 nm is incident normally on a surface, as shown in the diagram.
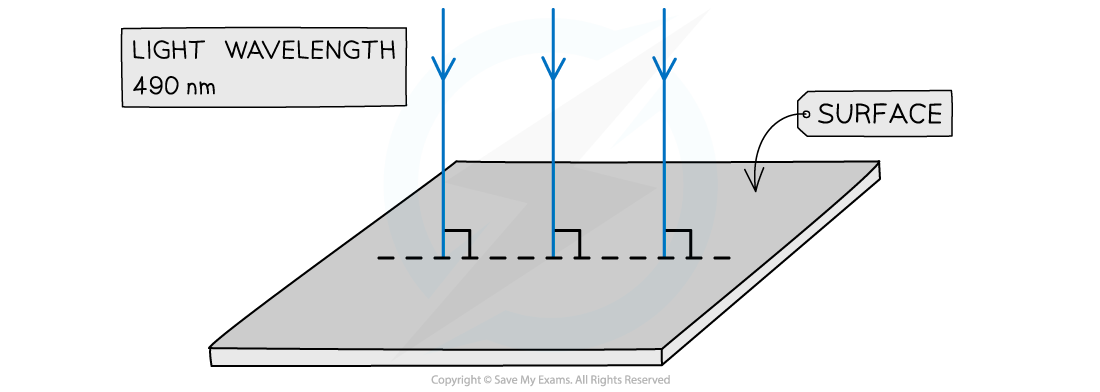
The power of the light is 3.6 mW. The light is completely absorbed by the surface.
Calculate the number of photons incident on the surface in 30 s.
Answer:
Step 1: Write down the known quantities
Wavelength, λ = 490 nm = 490 × 10−9 m
Power, P = 3.6 mW = 3.6 × 10−3 W
Time, t = 30 s
Step 2: Write the equation for photon energy and write in terms of wavelength
Step 3: Calculate the energy of one photon
Step 4: Calculate the number of photons hitting the surface every second
Step 5: Calculate the number of photons that hit the surface in 30 s
number of photons in 30 s = (8.87 × 1015) × 30 = 2.7 × 1017
Examiner Tips and Tricks
The values of Planck’s constant and the speed of light will be included in the data booklet, however, it helps to memorise them to speed up calculations!

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
