Decay Constant & Half-Life (DP IB Physics) : Revision Note
Decay Constant & Half-Life
Since radioactive decay is spontaneous and random, it is useful to consider the average number of nuclei that are expected to decay per unit time
This is known as the average decay rate
As a result, each radioactive element can be assigned a decay constant
The decay constant λ is defined as:
The probability that an individual nucleus will decay per unit of time
When a sample is highly radioactive, this means the number of decays per unit time is very high
This suggests it has a high level of activity
Activity, or the number of decays per unit time can be calculated using:
Where:
A = activity of the sample (Bq)
ΔN = number of decayed nuclei
Δt = time interval (s)
λ = decay constant (s-1)
N = number of nuclei remaining in a sample
The activity of a sample is measured in becquerels (Bq)
An activity of 1 Bq is equal to one decay per second, or 1 s-1
This equation shows:
The greater the decay constant, the greater the activity of the sample
The activity depends on the number of undecayed nuclei remaining in the sample
The minus sign indicates that the number of nuclei remaining decreases with time
Half-life and decay constant can be linked, using an equation called the exponential decay equation
This equation shows how the number of undecayed nuclei, N, changes over time, t, where N0 is the initial number of nuclei in the sample
When time t is equal to the half-life t½, the number of undecayed nuclei in the sample, N, will fall to half of its original value
The formula linking half-life and decay constant can then be derived as follows:
divide both sides by N0:
take the natural log of both sides:
apply properties of logarithms:
Therefore, half-life t½ can be calculated using the equation:
This equation shows that half-life t½ and the radioactive decay rate constant λ are inversely proportional
Therefore, the shorter the half-life, the larger the decay constant and the faster the decay
The half-life of a radioactive substance can be determined from decay curves and log graphs
Since half-life is the time taken for the initial number of nuclei, or activity, to reduce by half, it can be found by
Drawing a line to the curve at the point where the activity has dropped to half of its original value
Drawing a line from the curve to the time axis, this is the half-life
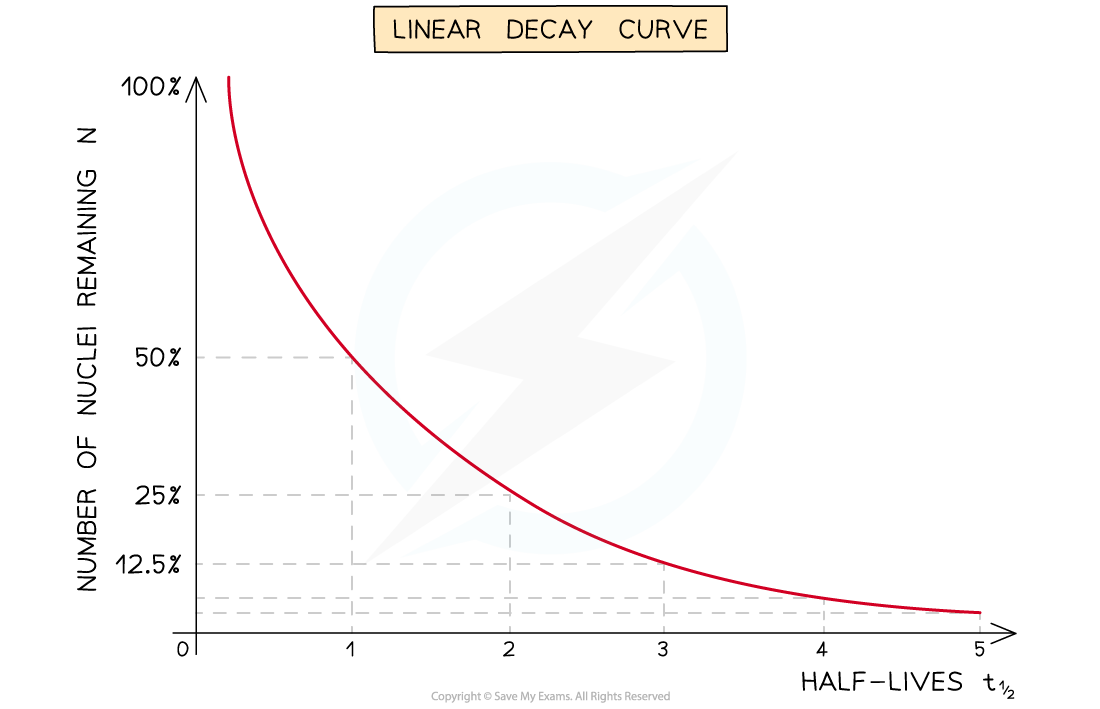
A linear decay curve. This represents the relationship:
Straight-line graphs tend to be more useful than curves for interpreting data
Due to the exponential nature of radioactive decay, logarithms can be used to achieve a straight-line graph
Take the exponential decay equation for the number of nuclei
Taking the natural logs of both sides
In this form, this equation can be compared to the equation of a straight line
Where:
ln N is plotted on the y-axis
t is plotted on the x-axis
gradient = −λ
y-intercept = ln N0
Half-lives can be found in a similar way to the decay curve but the intervals will be regular as shown below:

A logarithmic graph. This represents the relationship:
Note: experimentally, the measurement generally taken is the count rate of the source
Since count rate ∝ activity ∝ number of nuclei, the graphs will all take the same shapes when plotted against time (or number of half-lives) linearly or logarithmically
Worked Example
Radium is a radioactive element first discovered by Marie and Pierre Curie.
They used the radiation emitted from radium-226 to define a unit called the Curie (Ci) which they defined as the activity of 1 gram of radium.
It was found that in a 1 g sample of radium, 2.22 × 1012 atoms decayed in 1 minute.
Another sample containing 3.2 × 1022 radium-226 atoms had an activity of 12 Ci.
(a) Determine the value of 1 Curie
(b) Determine the decay constant for radium-226
Answer:
(a)
Step 1: Write down the known quantities
Number of atoms decayed, ΔN = 2.22 × 1012
Time, Δt = 1 minutes = 60 s
Step 2: Write down the activity equation

Step 3: Calculate the value of 1 Ci
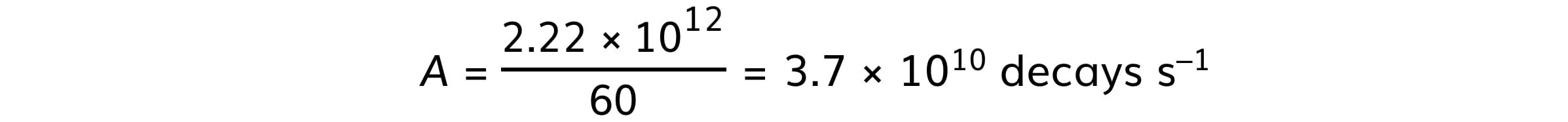
(b)
Step 1: Write down the known quantities
Number of atoms, N = 3.2 × 1022
Activity, A = 12 Ci = 12 × (3.7 × 1010) = 4.44 × 1011 Bq
Step 2: Write down the activity equation
A = λN
Step 3: Calculate the decay constant of radium
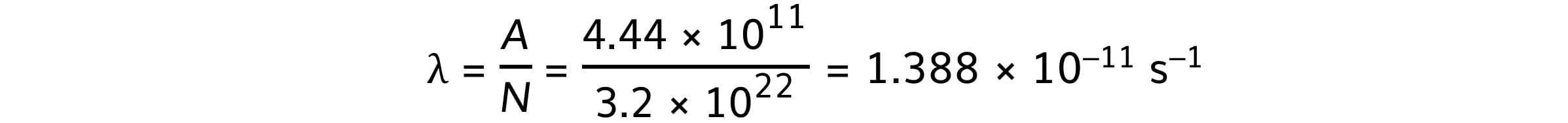
Therefore, the decay constant of radium-226 is 1.4 × 10–11 s–1
Worked Example
Strontium-90 is a radioactive isotope with a half-life of 28.0 years. A sample of Strontium-90 has an activity of 6.4 × 109 Bq.
(a) Calculate the decay constant λ, in year–1, of Strontium-90.
(b) Determine the fraction of the sample remaining after 50 years.
Answer:
(a)
Step 1: List the known quantities
Half-life, t½ = 28 years
Step 2: Write the equation for half-life
Step 3: Rearrange for λ and calculate
= 0.025 year−1
(b)
Step 1: List the known quantities
Decay constant, λ = 0.025 year−1
Time passed, t = 50 years
Step 2: Write the equation for exponential decay
Step 3: Rearrange for and calculate
= 0.287
Therefore, 28.7% of the sample will remain after 50 years

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
