The de Broglie Wavelength (DP IB Physics) : Revision Note
The de Broglie Wavelength
Louis de Broglie thought that if waves can behave like particles, then perhaps particles can also behave like waves
He proposed that electrons travel through space as waves
This would explain why they can exhibit wave-like behaviour such as diffraction
De Broglie suggested that electrons must also hold wave properties, such as wavelength
This came to be known as the de Broglie wavelength
However, he realised that all particles can show wave-like properties, not just electrons
He hypothesised that all moving particles have a matter wave associated with them
The definition of a de Broglie wavelength is:
The wavelength associated with a moving particle
De Broglie suggested that the momentum p of a particle and its associated wavelength λ are related by the equation:
Since momentum p = mv, the de Broglie wavelength can be related to the speed of a moving particle v by the equation:
Kinetic Energy & de Broglie Wavelength
Kinetic energy is defined as
Combining this with the previous equation gives relationship between the de Broglie wavelength of a particle to its kinetic energy:
Where:
λ = the de Broglie wavelength (m)
h = Planck’s constant (J s)
p = momentum of the particle (kg m s−1)
EK = kinetic energy of the particle (J)
m = mass of the particle (kg)
v = speed of the particle (m s−1)
Worked Example
A proton and an electron are each accelerated from rest through the same potential difference.
Determine the ratio:
Mass of a proton = 1.67 × 10–27 kg
Mass of an electron = 9.11 × 10–31 kg
Answer:

Evidence for the Wave Nature of Matter
The majority of the time, and for everyday objects travelling at normal speeds, the de Broglie wavelength is far too small for any quantum effects to be observed
A typical electron in a metal has a de Broglie wavelength of about 10 nm
Therefore, the quantum effects of diffraction will only be observable when the width of the aperture is of a similar size to the de Broglie wavelength
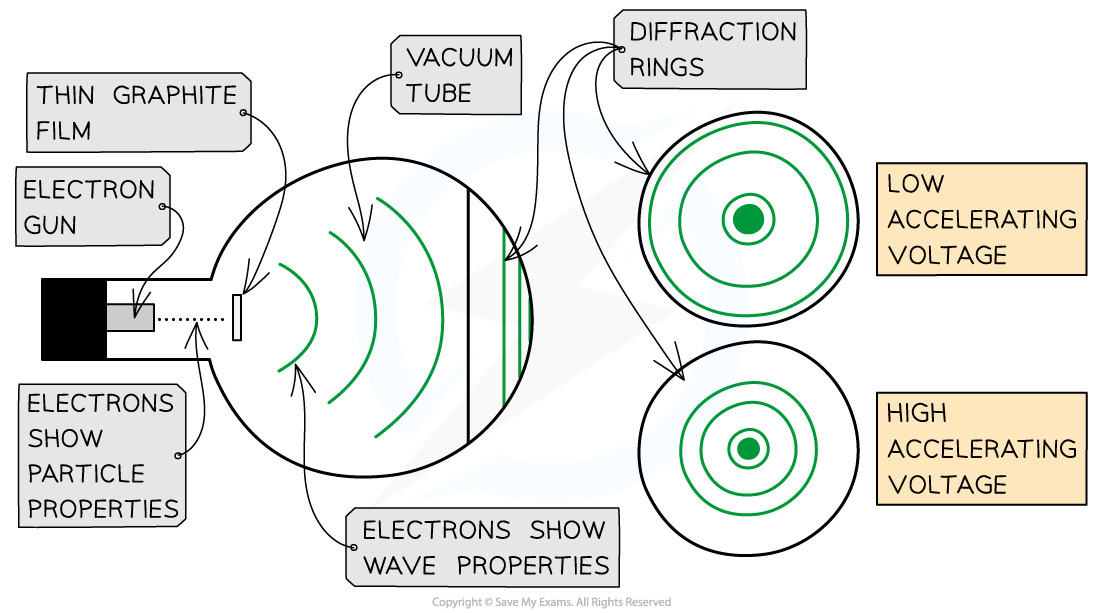
Electrons accelerated through a high potential difference demonstrate wave-particle duality
The electron diffraction tube can be used to investigate how the de Broglie wavelength of electrons depends on their speed
To observe the diffraction of electrons, they must be focused through a gap similar to their de Broglie wavelength, such as an atomic lattice
Graphite film is ideal for this purpose because of its crystalline structure
The gaps between neighbouring planes of the atoms in the crystals act as slits, allowing the electron waves to spread out and create a diffraction pattern
This phenomenon is similar to the diffraction pattern produced when light passes through a diffraction grating
If the electrons acted as particles, a pattern would not be observed, instead, the particles would be distributed uniformly across the screen. The diffraction pattern is observed on the screen as a series of concentric rings
It is observed that:
a larger accelerating voltage reduces the diameter of a given ring
a lower accelerating voltage increases the diameter of the rings
As the voltage is increased:
The speed of the electrons is increased, therefore:
the momentum of the electrons is increased
the kinetic energy of the electrons is increased
the de Broglie wavelength is decreased
The angle of diffraction is decreased, therefore:
the radius of the diffraction pattern is decreased
Electron diffraction was the first clear evidence that matter can behave like light and has wave properties
The de Broglie wavelength can be used to calculate the angle of the first maximum in the diffraction pattern
Where:
= angle of diffraction of the first maximum
= de Broglie wavelength
= spacing between atoms used for diffraction
The first minimum:
will be half the value of the first maximum
will not be zero
Subsequent minima reduce in intensity until reaching zero
Worked Example
Electrons are accelerated through a film of graphite. The electrons are accelerated through a potential difference of 40 V. The spacing between the graphite atoms is 2.1 × 10−10 m.
Calculate the angle of the first minimum of the diffraction pattern.
Answer:
Step 1: Determine the kinetic energy gained by an electron
Kinetic energy gained through a potential difference of 40 V = 40 eV
Step 2: Determine the speed of the electron
Step 3: Determine the de Broglie wavelength of the electron
Step 4: Determine the angle of the first maximum
Step 5: Determine the angle of the first minimum

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

