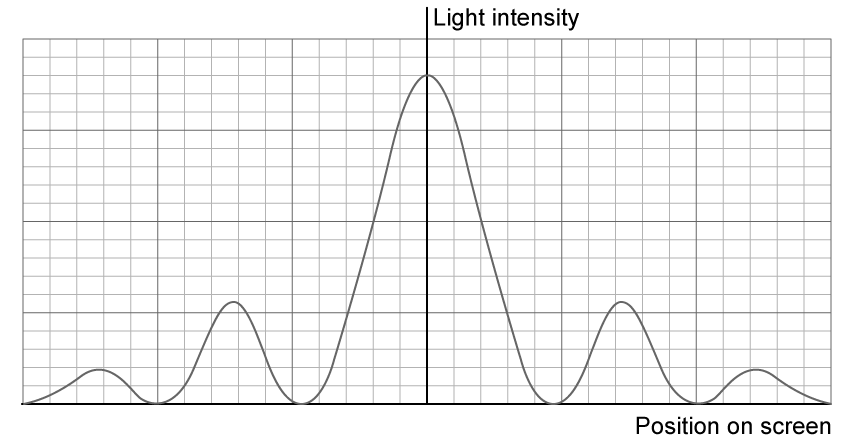
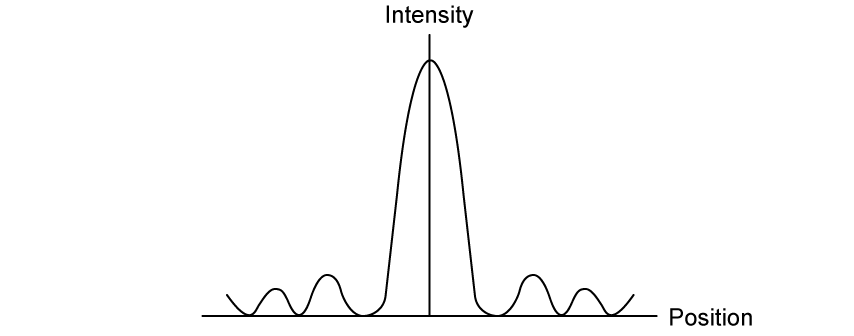
Outline what is meant by
(i) wavefront
[2]
(ii) ray.
[1]
Draw, on the grid below, scale diagrams showing the wavefronts for
(i) a plane wave with a wavelength of 1 cm
[2]
(ii) a circular wave with a wavelength of 1 cm.
[2]
In your diagrams, show the direction of propagation with arrows.

Did this page help you?