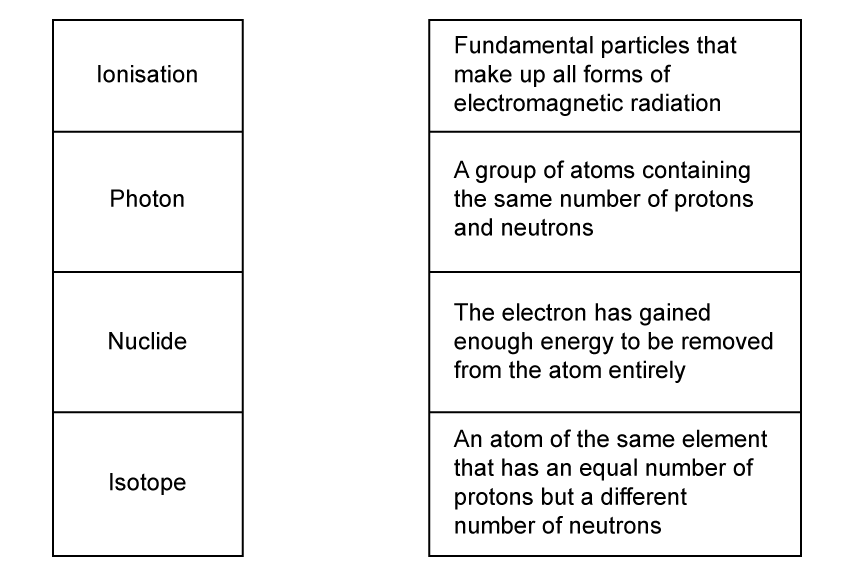
Match, by drawing a line, the words with their correct definitions.
The energy of a photon can be calculated using the equation
Define the following terms and give the unit:
Calculate the wavelength of a photon with an energy of 1.44 × 10−19 J.
Collisions with other atoms or electrons Releasing a photon Radioactive decay Absorbing a photon Changing colour Emitting a neutrino
A physical source, such as heat
[3]
Did this page help you?














