State Newton's Law of Gravitation.
Newton's Law of Gravitation can also be written in equation form:
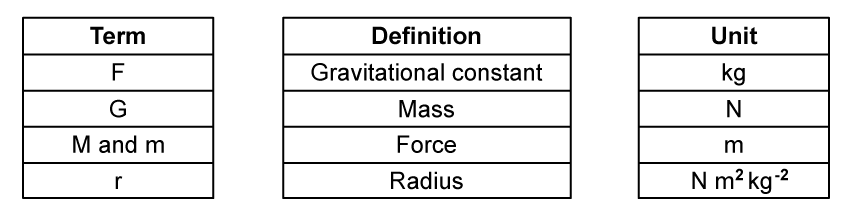
Match the terms in the equation with the correct definition and unit:
Newton's Law of Gravitation applies to point masses. Although planets are not point masses, the law also applies to planets orbiting the sun.
State why Newton's Law of Gravitation can apply to planets.
The mass of the Earth is 6.0 × 1024 kg. A satellite of mass 5000 kg is orbiting at a height of 8500 km above the centre of the Earth.
Calculate the gravitational force between the Earth and the satellite.
Did this page help you?





















