Single-Slit Diffraction (DP IB Physics): Revision Note
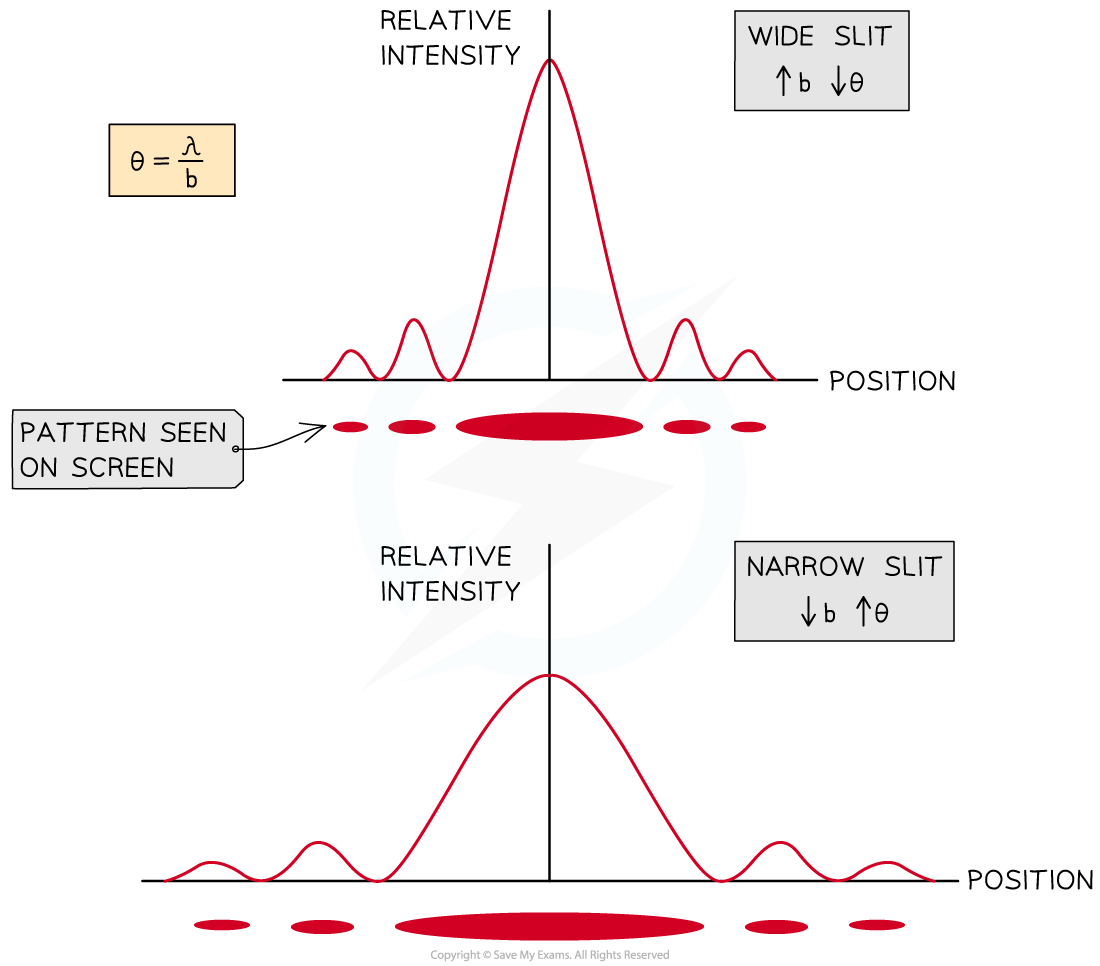
Single Slit Intensity Pattern
When monochromatic light passes through a single rectangular slit, a diffraction pattern can be observed on a faraway screen
This pattern, similar to the double slit interference pattern, contains:
bright fringes of maximum intensity, produced by constructive interference
dark fringes of zero or minimum intensity, produced by destructive interference
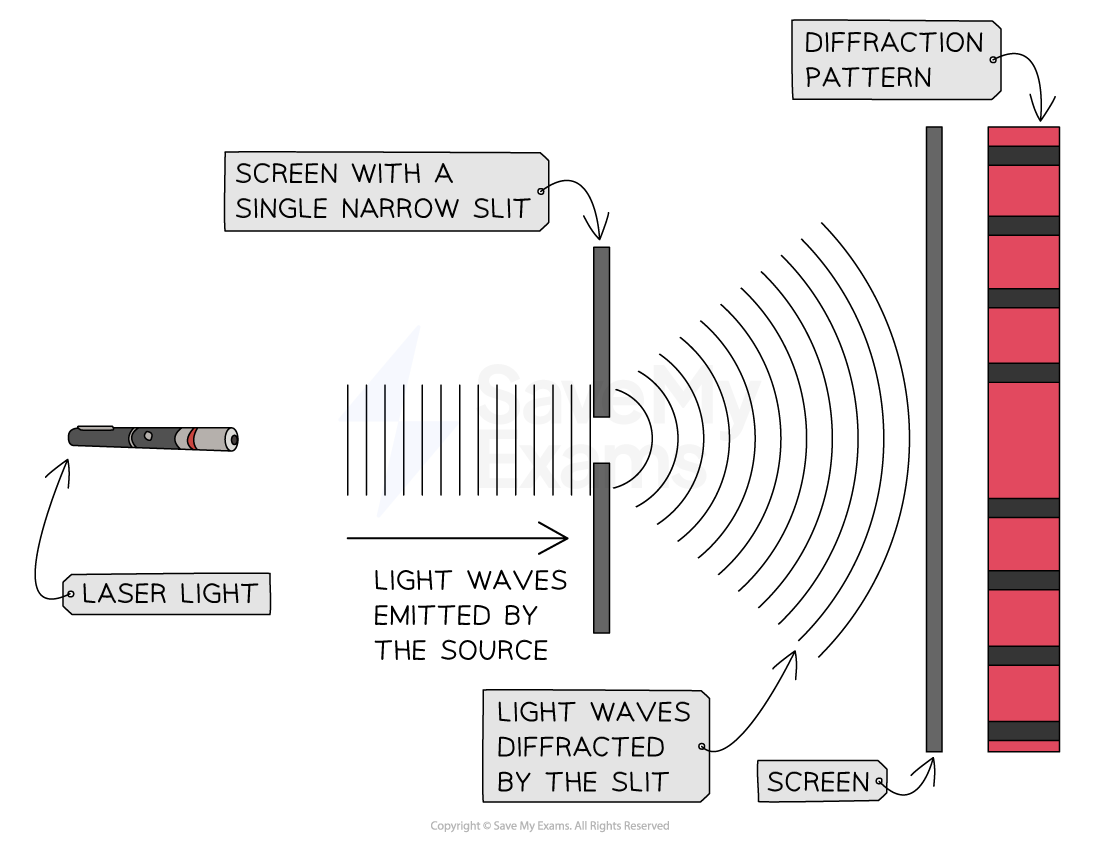
However, the single-slit diffraction and double-slit interference patterns are slightly different
The central maximum of the single-slit diffraction pattern is:
wider and brighter than the other bright fringes
wider than that of the double-slit interference pattern
On either side of the wide central maxima for the single slit diffraction pattern are much narrower and less bright maxima
These get dimmer as the order increases
Features of the single-slit intensity pattern
If a laser emitting blue light is directed at a single slit, where the slit width is similar in size to the wavelength of the light, its intensity pattern will be as follows:
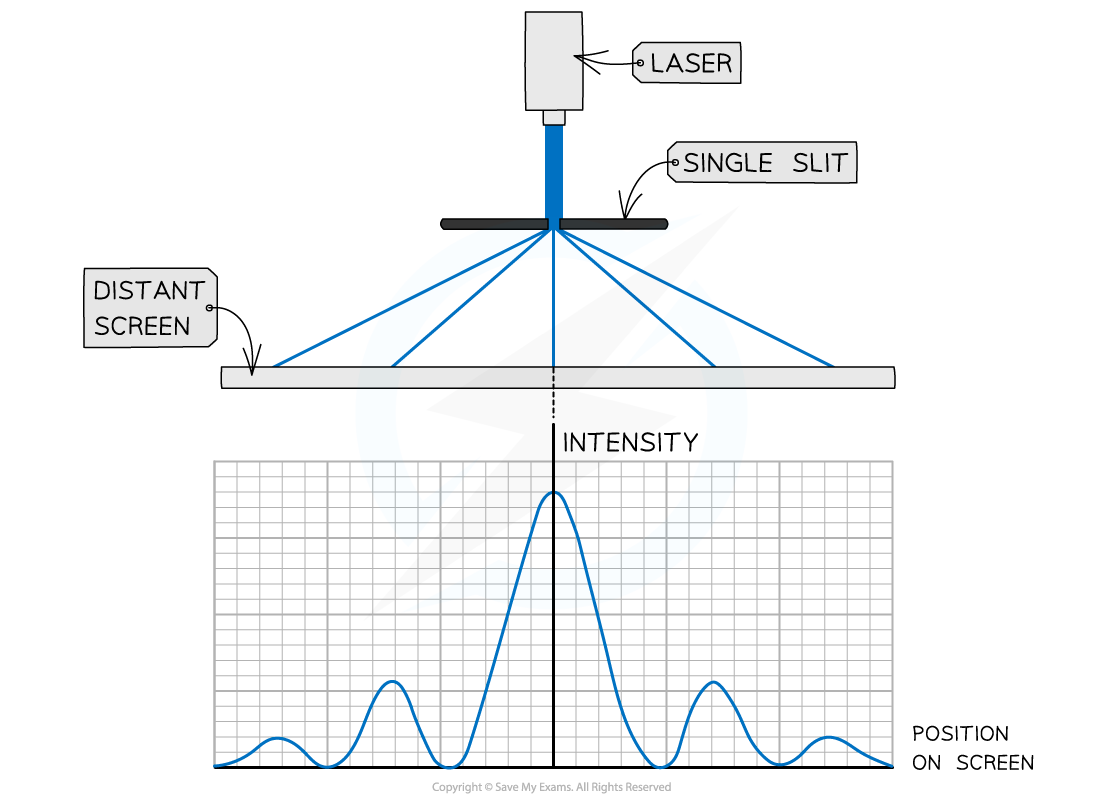
The features of the single slit intensity pattern are:
the central bright fringe has the greatest intensity of any fringe and is called the central maximum
the dark fringes are regions with zero intensity
the intensity of each bright fringe gradually decreases on either side of the central maxima
Effect of changing wavelength
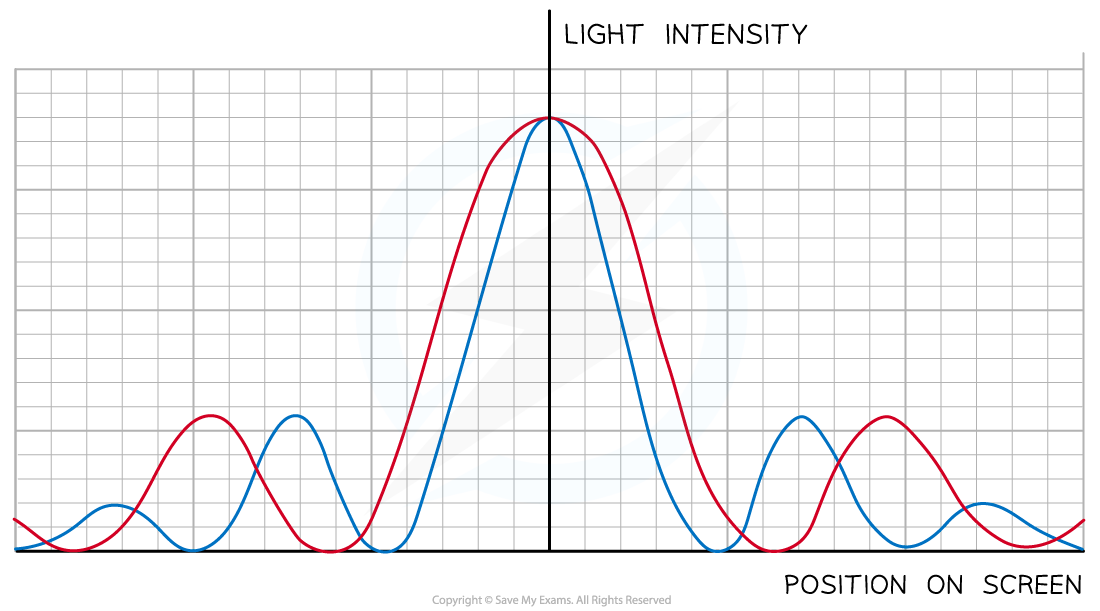
If the wavelength passing through the gap increases, the wave diffracts more
This means the angle of diffraction of the waves increases as they pass through the slit
As a result, the width of the bright maxima also increases
Red light
has the longest wavelength on the visible light spectrum
produces a diffraction pattern with wider fringes (due to a larger angle of diffraction)
Blue light
has a shorter wavelength on the visible light spectrum
produces a diffraction pattern with narrower fringes (due to a smaller angle of diffraction)
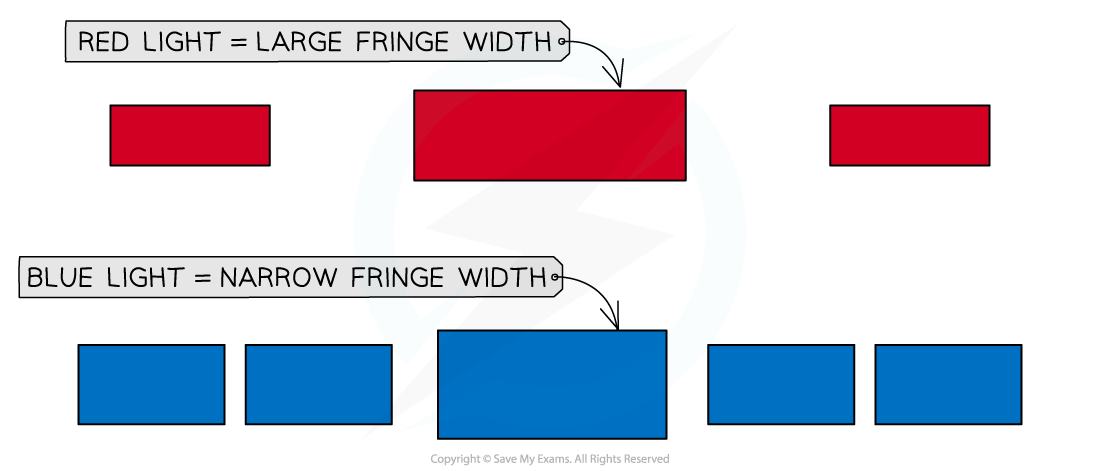
If the blue laser is replaced with a red laser:
the light diffracts more as the waves pass through the single slit
the fringes in the intensity pattern appear wider
Effect of changing slit width
If the slit is made narrower:
the angle of diffraction is greater
the waves spread out more beyond the slit
For a narrower slit, the intensity graph shows that:
the intensity of the maxima decreases
the width of the central maxima increases
the spacing between fringes is wider
Single slit diffraction equation
These properties of wavelength and slit width for single slit diffraction for the first minimum can be explained using the equation:
Where:
= the angle of diffraction of the first minimum (°)
= wavelength of incident light (m)
= slit width (m)
This equation tells us:
the longer the wavelength of light, the larger the angle of diffraction
the narrower the slit width then the larger the angle of diffraction
Single slit geometry
The diffraction pattern made by waves passing through a slit of width
can be explained by considering Huygen's principle, in which
each point on a wavefront acts as a source of secondary waves, or wavelets
the wavelets are coherent and interfere with each other
The central maximum is produced by:
wavelets travelling straight forward
constructive interference due to all wavelets travelling the same distance
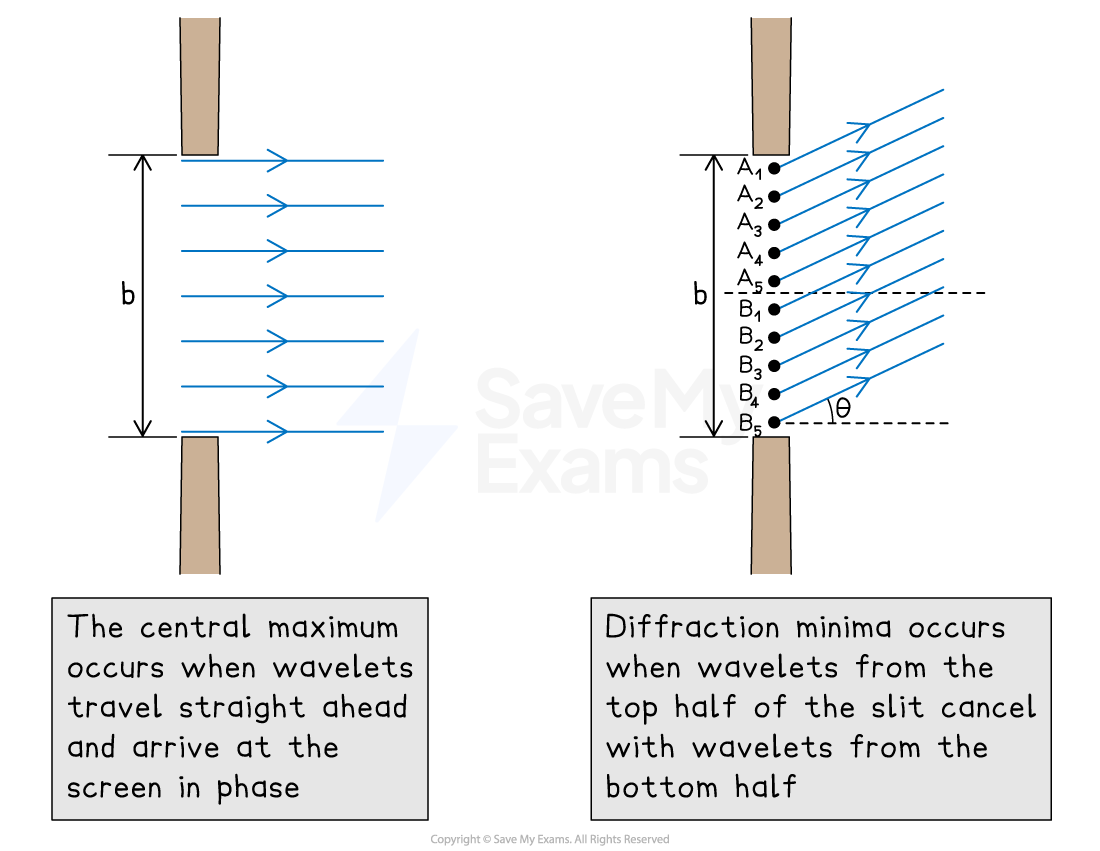
Position of the first minimum
For wavelets travelling to the first minimum at an angle
to the centre line (which splits the slit in half):
the wavelets on one half of the slit will travel a greater distance than the wavelets on the other half
if all the wavelets from one half cancel out all the wavelets from the other half, this will result in a dark region (destructive interference)
Every point on the wavefront can be paired with another point a distance
away
For all the wavelet pairs to cancel (or interfere destructively), the path difference must be

If the distance
between the slit and the screen is considerably larger than the slit width,
:
the waves can be considered to travel nearly parallel to each other
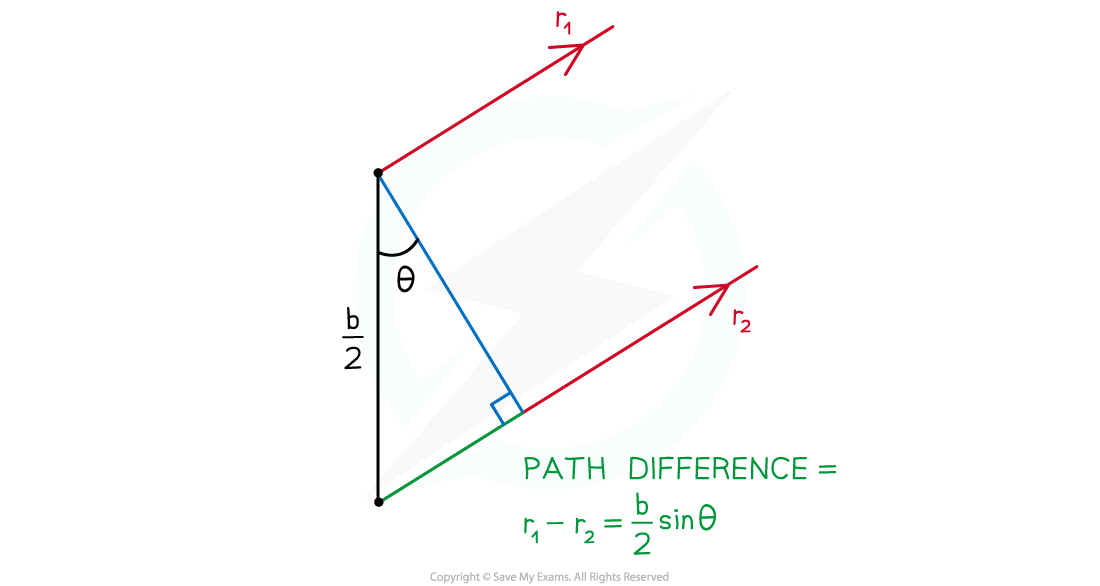
For two rays,
and
, travelling parallel to each other at an angle
between the normal and the slit, where:
emerges from the top edge of the slit
emerges from the centre of the slit, exactly halfway down
The path difference is the extra distance travelled by
, which is equal to:
path difference =
For the two rays,
and
, to interfere destructively:
path difference =
Therefore, the angle of the first minimum occurs when:
Since the distance between the slit and the screen is much larger than the slit width
, the angle
is very small
Therefore, the small-angle approximation
can be applied:
This leads to the equation for the angle of diffraction of the first minimum:
Using similar reasoning, additional minima occur at:
Where
= 1, 2, 3... etc.
Note: In general, the condition for destructive interference for single slit diffraction can be described by
. This expression should be used for angles at which the small-angle approximation is not valid
Width of the central maximum
The central maximum extends from the centre to the first minimum on each side
The distance to the first minimum can be found using trigonometry
Where
= angle of the first minimum (rad)
= distance from the centre to the first minimum (m)
= distance from the slit to the screen (m)
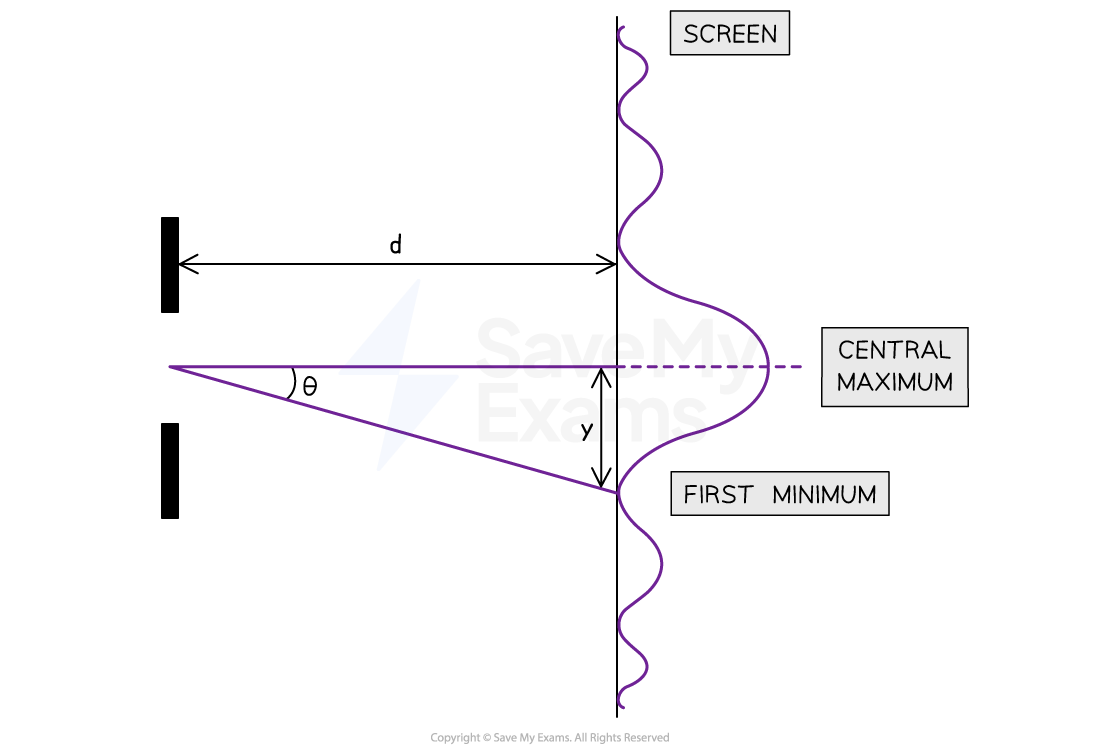
Using the small-angle approximation
:
The total width of the central maximum is equal to
, which gives:
Substituting the expression for the angle of the first minimum:
Worked Example
A group of students are performing a diffraction investigation where a beam of coherent light is incident on a single slit with width .
The light is then incident on a screen which has been set up a distance away.

A pattern of light and dark fringes is seen.
The teacher asks the students to change their setup so that the width of the first bright maximum increases.
Suggest three changes the students could make to the set-up of their investigation which would achieve this.
Answer:
Step 1: Write down the equation for the angle of diffraction
The width of the fringe is related to the size of the angle of diffraction
Step 2: Use the equation to determine the factors that could increase the width of each fringe
Change 1:
The angle of diffraction
is inversely proportional to the slit width
Therefore, reducing the slit width would increase the fringe width
Change 2:
The angle of diffraction
is directly proportional to the wavelength
Therefore, increasing the wavelength of the light would increase the fringe width
Change 3:
The distance between the slit and the screen will also affect the width of the central fringe
A larger distance means the waves must travel further, hence, they will spread out more
Therefore, moving the screen further away would increase the fringe width
Examiner Tips and Tricks
Make sure you have a good understanding of the models and assumptions made in single slit geometry, i.e. Huygens' principle, parallel rays, and the small angle approximation.
When applying the small-angle approximation , keep in mind:
must be in radians, not degrees
it is most accurate for angles of
or less
Double Slit Modulation
When light passes through a double slit, two types of interference occur:
The diffracted rays passing through one slit interfere with the rays passing through the other
Rays passing through the same slit interfere with each other
This produces a double-slit intensity pattern where the single-slit intensity pattern modulates (adjusts) the intensity of the light on the screen
The single-slit intensity pattern has a distinctive central maximum and subsequent maxima at lower intensity
The double-slit interference pattern has equally spaced intensity peaks with maxima of equal intensity
Together, the combined double slit intensity pattern has equally spaced bright fringes, but now within a single slit 'envelope'
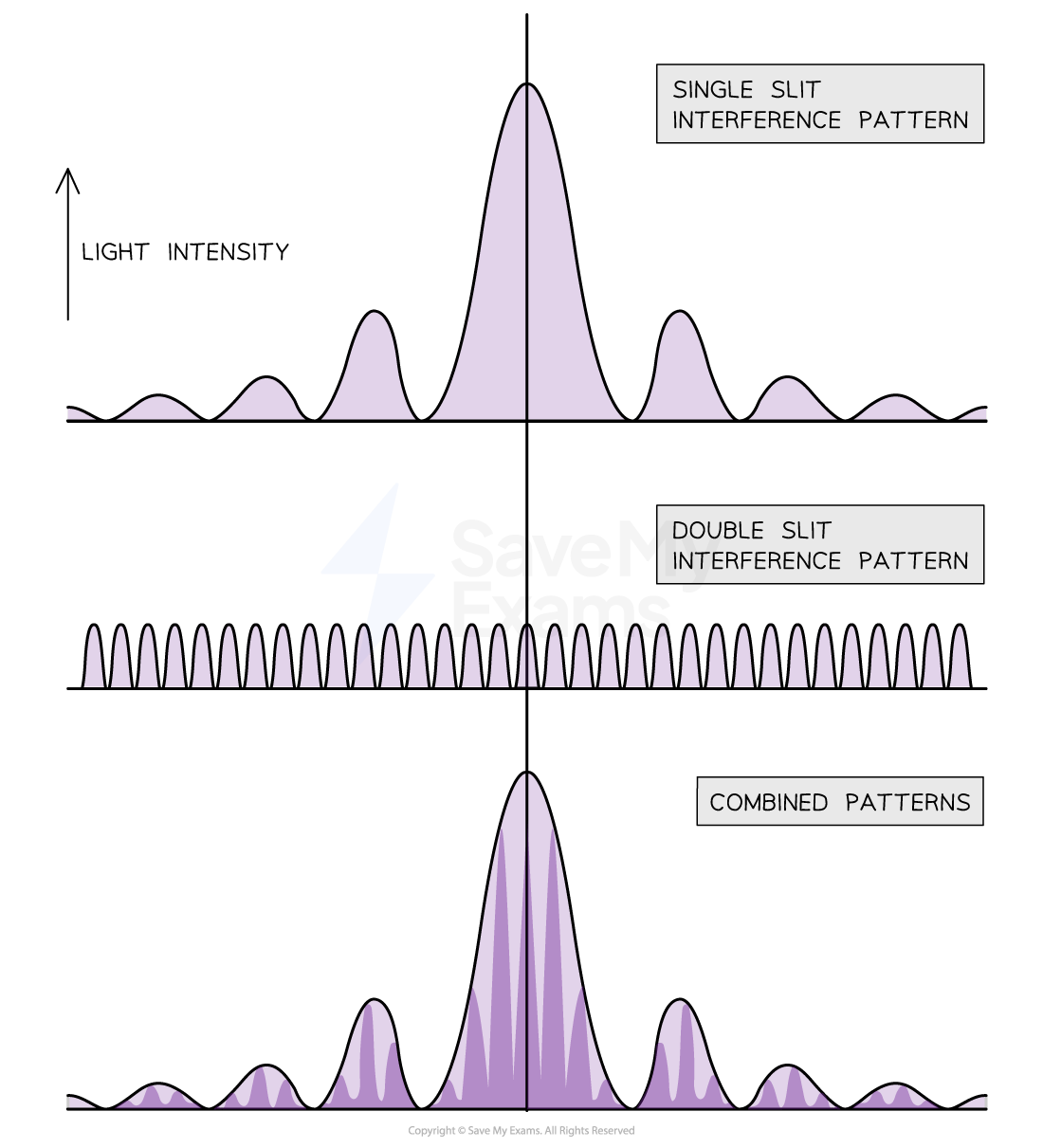
This is assuming that:
The slit width is not negligible
The distance between the slits is much greater than their width

Unlock more, it's free!
Did this page help you?