Binding Energy per Nucleon Curve (DP IB Physics: HL)

• In order to compare nuclear stability, it is more useful to look at the binding energy per nucleon
• The binding energy per nucleon is defined as:

The binding energy of a nucleus divided by the number of nucleons in the nucleus

• A higher binding energy per nucleon indicates a higher stability
  • In other words, it requires more energy to pull the nucleus apart

• Iron (A = 56) has the highest binding energy per nucleon, which makes it the most stable of all the elements

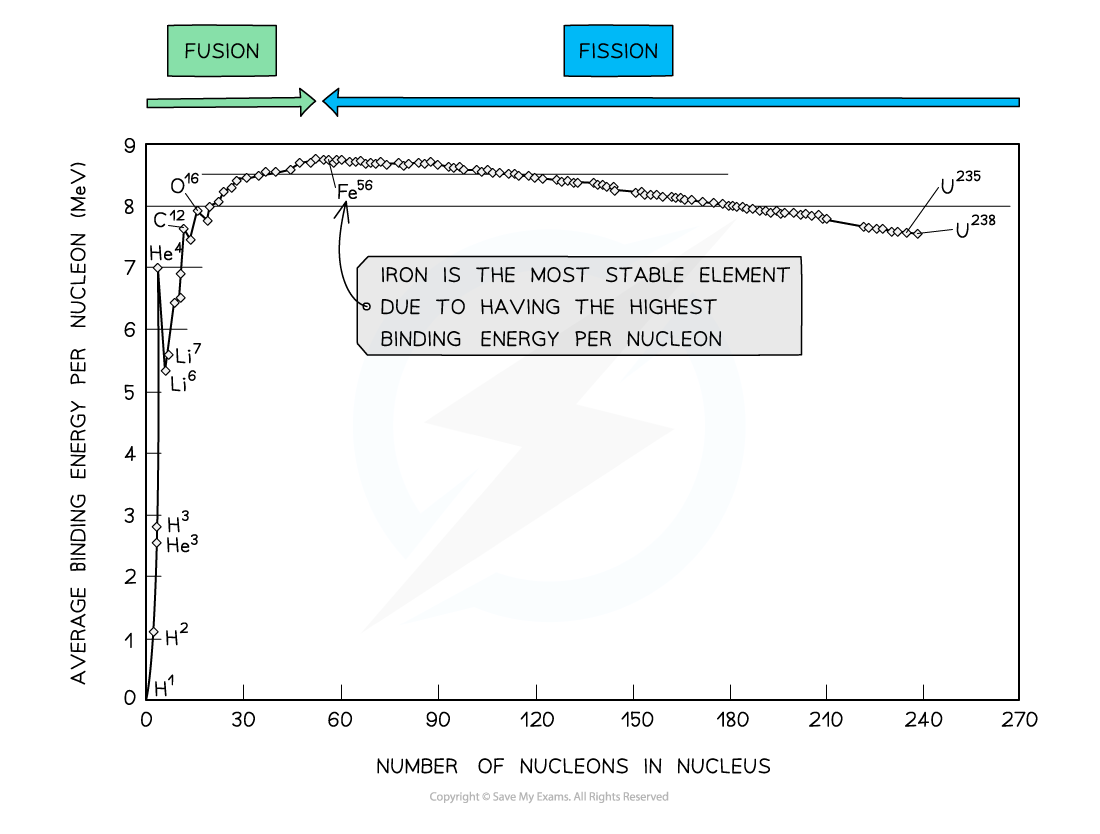
By plotting a graph of binding energy per nucleon against nucleon number, the stability of elements can be inferred

Key Features of the Graph

• At low values of A:
  • Nuclei tend to have a lower binding energy per nucleon, hence, they are generally less stable
  • This means the lightest elements have weaker electrostatic forces and are the most likely to undergo fusion

• Helium (⁴He), carbon (¹²C) and oxygen (¹⁶O) do not fit the trend
  • Helium-4 is a particularly stable nucleus hence it has a high binding energy per nucleon
  • Carbon-12 and oxygen-16 can be considered to be three and four helium nuclei, respectively, bound together

• At high values of A:
  • The general binding energy per nucleon is high and gradually decreases with A
  • This means the heaviest elements are the most unstable and likely to undergo fission

Comparing Fusion & Fission

• Fusion occurs at low values of A because:
  • Attractive nuclear forces between nucleons dominate over repulsive electrostatic forces between protons

• In fusion, the mass of the nucleus that is created is slightly less than the total mass of the original nuclei
  • The mass defect is equal to the binding energy that is released since the nucleus that is formed is more stable

• Fission occurs at high values of A because:
  • Repulsive electrostatic forces between protons begin to dominate, and these forces tend to break apart the nucleus rather than hold it together

• In fission, an unstable nucleus is converted into more stable nuclei with a smaller total mass
  • This difference in mass, the mass defect, is equal to the binding energy that is released

• Fusion releases much more energy per kg than fission
• The energy released is the difference in binding energy caused by the difference in mass between the reactant and products
  • Hence, the greater the increase in binding energy, the greater the energy released

• At small values of A (fusion region), the gradient is much steeper compared to the gradient at large values of A (fission region)
• This corresponds to a larger binding energy per nucleon being released

Step 1: Calculate the mass defect Δm

Number of protons, Z = 26

Number of neutrons, A – Z = 56 – 26 = 30

Mass defect, Δm = Zm_p + (A – Z)m_n – m_total

Δm = (26 × 1.673 × 10^–27) + (30 × 1.675 × 10^–27) – (9.288 × 10^–26)

Δm = 8.680 × 10^–28 kg

Step 2: Calculate the binding energy E of the nucleus

Binding energy, E = Δmc²

E = (8.680 × 10^–28) × (3.00 × 10⁸)² = 7.812 × 10^–11 J

Step 3: Calculate the binding energy per nucleon

Binding energy per nucleon = 

Step 4: Convert to MeV

J → eV: multiply by 6.2 × 10^-18

eV → MeV: divide by 10⁶

Binding energy per nucleon

Part (a)

Step 1: Use the graph to identify each isotope’s binding energy per nucleon

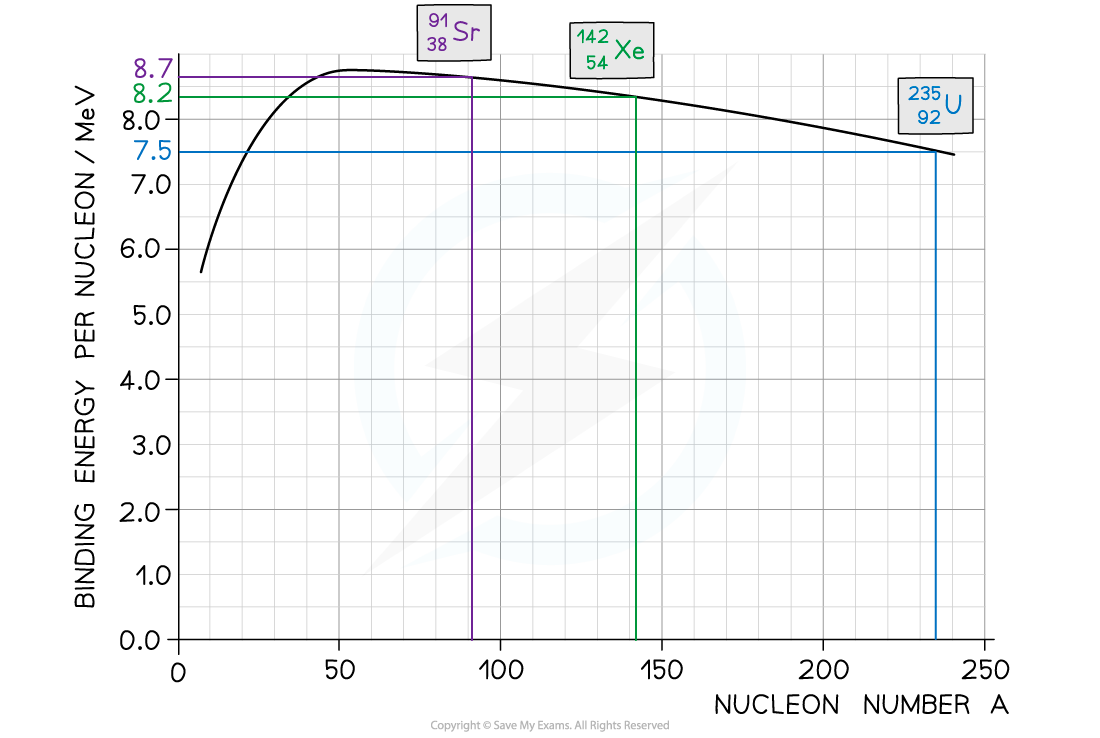
• • Binding energy per nucleon (U-235) = 7.5 MeV
  • Binding energy per nucleon (Sr-91) = 8.2 MeV
  • Binding energy per nucleon (Xe-142) = 8.7 MeV

Step 2: Determine the binding energy of each isotope

Binding energy = Binding Energy per Nucleon × Mass Number

• • Binding energy of U-235 nucleus = (235 × 7.5) = 1763 MeV
  • Binding energy of Sr-91 = (91 × 8.2) = 746 MeV
  • Binding energy of Xe-142 = (142 × 8.7) = 1235 MeV

Step 3: Calculate the energy released

Energy released = Binding energy after (Sr + Xe) – Binding energy before (U)

Energy released = (1235 + 746) – 1763 = 218 MeV

Part (b)

Step 1: Calculate the energy released by 1 mol of uranium-235

• • There are N_A (Avogadro’s number) atoms in 1 mol of U-235, which is equal to a mass of 235 g
  • Energy released by 235 g of U-235 = (6 × 10²³) × 218 MeV

Step 2: Convert the energy released from MeV to J

• • 1 MeV = 1.6 × 10^–13 J
  • Energy released = (6 × 10²³) × 218 × (1.6 × 10^–13) = 2.09 × 10¹³ J

Step 3: Work out the proportion of uranium-235 in the sample

• • 1 kg of uranium which is 3% U-235 contains 0.03 kg or 30 g of U-235

Step 4: Calculate the energy released by the sample

Energy released from 1 kg of Uranium =