Properties of Waves (DP IB Physics: HL)

• Travelling waves are defined as follows:

Oscillations that transfer energy from one place to another without transferring matter

• Energy is transferred by the waves, but matter is not
• The direction of the motion of the wave is the direction of the energy transfer
• Travelling waves can be of two types:
  • Mechanical Waves, which propagate through a medium and cannot take place in a vacuum
  • Electromagnetic Waves, which can travel through a vacuum

• Waves are generated by oscillating sources 
  • These oscillations travel away from the source

• Oscillations can propagate through a medium (e.g. air, water) or in vacuum (i.e. no particles), depending on the type of wave

• The key properties of travelling waves are as follows:

• Displacement (x) of a wave is the distance of a point on the wave from its equilibrium position
  • It is a vector quantity; it can be positive or negative
  • Measured in metres (m)

• Wavelength (λ) is the length of one complete oscillation measured from same point on two consecutive waves 
  • For example, two crests, or two troughs
  • Measured in metres (m)

• Amplitude (x₀) is the maximum displacement of an oscillating wave from its equilibrium position (x = 0)
  • Amplitude can be positive or negative depending on the direction of the displacement 
  • Measured in metres (m)

• Period (T) is the time taken for a fixed point on the wave to undergo one complete oscillation
  • Measured in seconds (s)

• Frequency (f) is the number of full oscillations per second
  • Measured in Hertz (Hz)

• Wave speed (c) is the distance travelled by the wave per unit time
  • Measured in metres per second (m s^-1)

Diagram showing the amplitude and wavelength of a wave

• The frequency, f, and the period, T, of a travelling wave are related to each other by the equation:

Period T and frequency f of a travelling wave

(i) Identify the amplitude A of the wave on the graph 

• • The amplitude is defined as the maximum displacement from the equilibrium position (x = 0)

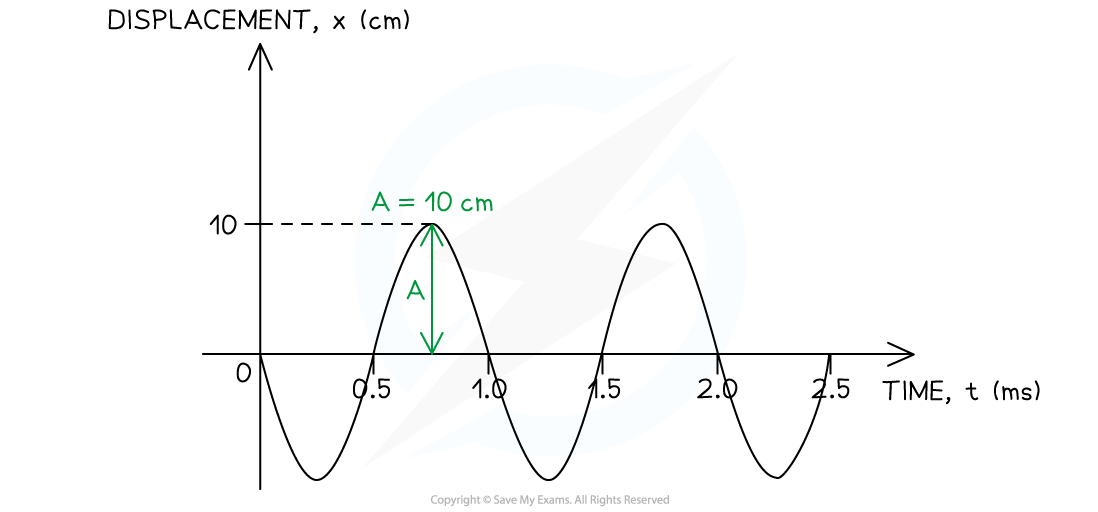
• • The amplitude must be converted from centimetres (cm) into metres (m)

A = 0.1 m

(ii) Calculate the frequency of the wave

Step 1: Identify the period T of the wave on the graph 

• • The period is defined as the time taken for one complete oscillation to occur

• • The period must be converted from milliseconds (ms) into seconds (s)

T = 1 × 10^–3 s

Step 2: Write down the relationship between the frequency f and the period T 

Step 3: Substitute the value of the period determined in Step 1

f = 1000 Hz

• The wave equation describes the relationship between the wave speed, the wavelength and the frequency of the wave

c = fλ

• Where
  • c = wave speed in metres per second (m s⁻¹)
  • f = frequency in hertz (Hz)
  • λ = wavelength in metres (m)

Deriving the Wave Equation

• The wave equation can be derived using the equation for speed

v = 

• Where
  • v = velocity or speed in metres per second (m s⁻¹)
  • d = distance travelled in metres (m)
  • t = time taken in seconds (s)

• When the source of a wave undergoes one complete oscillation, the travelling wave propagates forward by a distance equal to one wavelength λ

• The travelling wave covers this distance in the time it takes the source to complete one oscillation, the time period T

wave speed =  = 

• Therefore, the wave speed c  is given by

c = 

• The period T of a wave is given by:

T = 

• Therefore, combining these equations gives the wave equation

c = fλ

Step 1: Write down the known quantities

• • Period, T = 1.0 μs = 1.0 × 10^–6 s
  • Velocity, c = 100 cm s^–1 = 1.0 m s^–1

Note the conversions:

• • The period must be converted from microseconds (μs) into seconds (s)
  • The velocity must be converted from cm s^–1 into m s^–1

Step 2: Write down the relationship between the frequency f and the period T 

Step 3: Substitute the value of the period into the above equation to calculate the frequency 

f = 1.0 × 10⁶ Hz

Step 4: Write down the wave equation

c = fλ

Step 5: Rearrange the wave equation to calculate the wavelength λ

Step 6: Substitute the numbers into the above equation 

λ = 1 × 10^–6 m