Specific Heat Capacity (DP IB Physics) : Revision Note
Specific Heat Capacity
The amount of thermal energy needed to change the temperature of an object depends on:
The change in temperature required ΔT, i.e. the larger the change in temperature the more energy is needed
The mass of the object m, i.e. the greater the mass the more energy is needed
The specific heat capacity c of the given substance, i.e. the higher the specific heat capacity the more energy is needed
Substance | Specific Heat Capacity (J kg−1 K−1) |
|---|---|
Water | 4200 |
Ice | 2200 |
Aluminium | 900 |
Copper | 390 |
Gold | 130 |
The equation for the thermal energy transferred, Q, is then given by
Where:
m = mass of the substance (kg)
ΔT = change in temperature (K or °C)
c = specific heat capacity of the substance (J kg–1 K–1)
The specific heat capacity of a substance is defined as:
The amount of energy required to change the temperature of 1 kg of a substance by 1 K (or 1°C)
This definition can be explained when the above equation is rearranged for c:
This means the higher the specific heat capacity of a substance, the longer it takes for the substance to warm up or cool down
Note that the specific heat capacity is measured in J kg–1 K–1
Specific heat capacity of water and copper
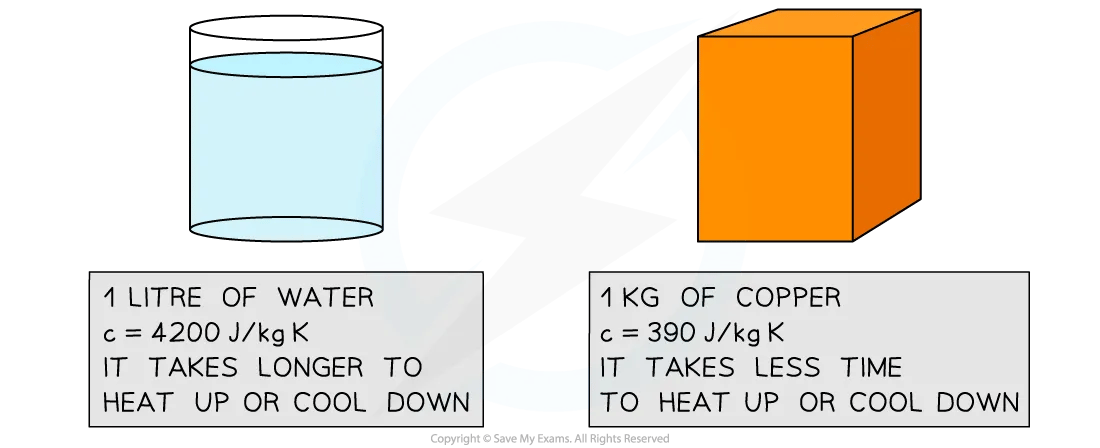
The high specific heat capacity of water means it heats up and cools down much slower than metals, such as copper
Worked Example
A piece of copper of mass 50 g is heated until it reaches a temperature of 120 °C. The copper is removed from the heat and immediately placed into 250 mL of water at 25 °C.
The temperature of the water and copper is measured until they reach thermal equilibrium.
Determine the final temperature of the copper and water, in degrees Celsius (°C), assuming no heat is lost to the surroundings.
The specific heat capacity of water is 4200 J kg–1 K–1
The specific heat capacity of copper is 390 J kg–1 K–1
Answer:
Step 1: Write down the known quantities
Mass of copper, mc = 50 g = 0.05 kg
Mass of water, mw = 250 ml = 0.25 kg (since 1 litre = 1 kg)
Initial temperature of copper, Tc = 120 °C
Initial temperature of water, Tw = 25°C
Specific heat capacity of water, cw = 4200 J kg–1 K–1
Specific heat capacity of copper, cc = 390 J kg–1 K–1
Step 2: Write down the equation for thermal energy
Step 3: Equate the equations for the energy transferred from the copper to the water
The copper is at a higher initial temperature than the water, hence thermal energy will be transferred from the copper to the water
The energy lost by the copper = the energy gained by the water
Step 4: Determine the final temperature Tf of the copper and water
Since the water and copper reach thermal equilibrium, their final temperature Tf will be the same
Examiner Tips and Tricks
You should notice that changes in temperature ΔT can usually be written in degrees Celsius (although this is not the SI base unit for temperature) and do not need to be converted into kelvin (K). This is because differences in absolute temperatures always correspond to differences in Celsius temperature.
If the question asks to determine the initial or final temperature of a substance, make sure you always check the unit of measure (°C or K) in which you are required to give your final answer.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
