Quantization of Angular Momentum (DP IB Physics: HL)

• Angular momentum is a property of any spinning or rotating body, very similar to linear momentum
  • In linear motion, momentum is the product of mass and velocity
• In rotational motion the momentum is the product of moment of inertia and angular speed

• Angular momentum is a vector, this means:
  • The magnitude is equal to the momentum of the particle times its radial distance from the centre of its circular orbit
  • The direction of the angular momentum vector is normal to the plane of its orbit with the direction being given by the corkscrew rule

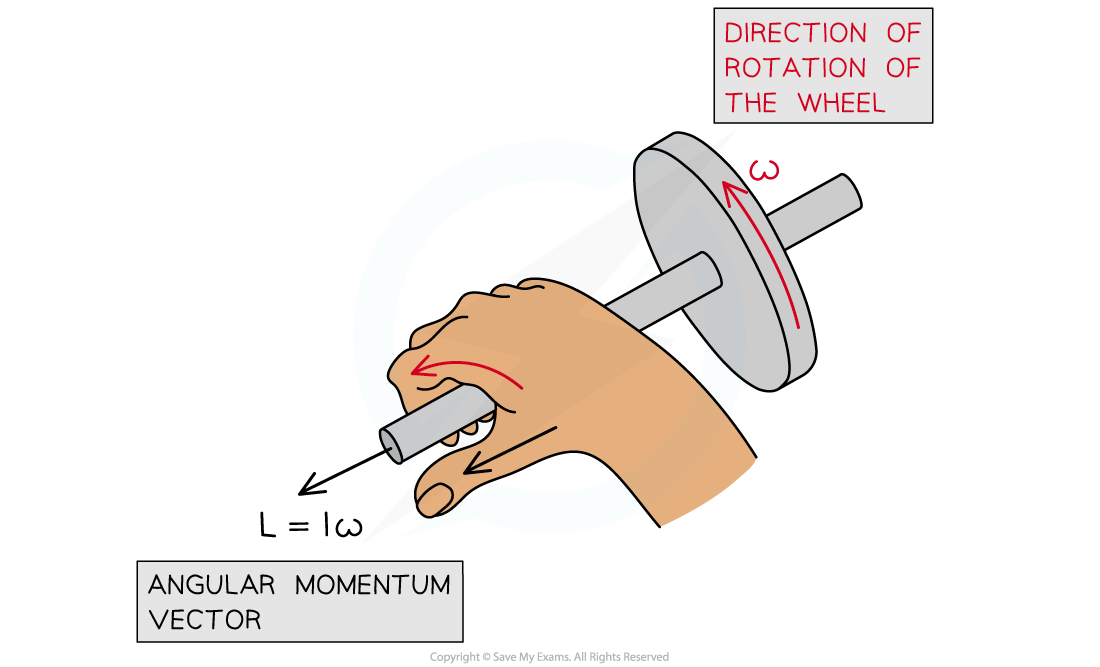
Angular momentum acts at right angles to the direction of rotation

• Niels Bohr proposed that the angular momentum, L, of an electron in an energy level is quantised in integer multiples of
• Where:
  • n = an integer (n = 1, 2, 3...)
  • h = Planck’s constant
• Sometimes h may be written as the reduced Planck's constant, ħ, which is equal to

• Hence the angular momentum for an electron in a circular orbit is constant

• De Broglie proposed that an electron with momentum p = mv has a wavelength λ given by

• For an electron moving in a straight line, the matter wave takes a familiar wave shape consisting of peaks and troughs
  • Although the electron itself isn't oscillating up and down, only the matter wave

de Broglie matter wave for an electron moving in a straight line at constant speed

• For the same electron moving in a circle, the matter wave still has a sinusoidal shape but is wrapped into a circle

de Broglie matter wave for an electron moving in a circular orbit at constant speed

• As the electron continues to orbit in a circle two possibilities may occur:

 1. On completing one oscillation, the waves overlap in phase

• • The waves will continue in phase over many orbits giving rise to constructive interference and a standing wave 

de Broglie matter wave where 3λ is less than the orbits circumference

• • In other words, peak overlaps with peak, trough with trough
  • This means that where the waves overlap, destructive interference occurs and as a result, no such electron orbit is allowed

de Broglie matter wave where n = 3. Here the circumference of the circular orbit is 3λ

• Hence, the circumference of the orbit  must equal an integer number of wavelengths  for a standing wave to form:

• Using the de Broglie relation, :

• Since momentum is equal to :

• Rearranging for angular momentum, :

Bohr Condition

• The Bohr Condition is given by the relation:

• Where:
  • n = energy level 
  • h = Planck's constant (J s)
  • m = mass (kg)
  • v = velocity (m s^–1)
  • r = radius (m)
• The condition essentially states that an electron can only move in fixed orbits
• Neils Bohr and Ernest Rutherford found that atomic orbits are only allowed when:
  • The angular momentum of the electron is an integer multiple of 
• The Bohr condition also leads to the restriction of the electron radius to certain values 
• Another implication is that the discrete or quantised energy of the electron follows this rule:

eV

Step 1: List the known quantities

• • Mass of an electron, m = 9.1 × 10⁻³¹ kg
  • Radius of the orbit, r = 0.529 × 10⁻¹⁰ m
  • Planck's constant, h = 6.63 × 10⁻³⁴ kg m² s^-1

Step 2: Write the Bohr Condition equation and rearrange for velocity, v

Step 3: Substitute in the values and calculate, v

Step 4: Write the final answer

The velocity of the electron = 2.2 × 10⁶ m s^-1