Faraday’s Law of Induction (DP IB Physics): Revision Note
Faraday’s Law of Induction
Faraday's law of induction relates the rate of change of magnetic flux linkage with the e.m.f. induced in a conductor
It is defined in words as:
The magnitude of an induced e.m.f is directly proportional to the rate of change of magnetic flux linkage
Faraday's law is defined by the equation:
Where:
= induced e.m.f (V)
= change in magnetic flux linkage (Wb turns)
= time interval (s)
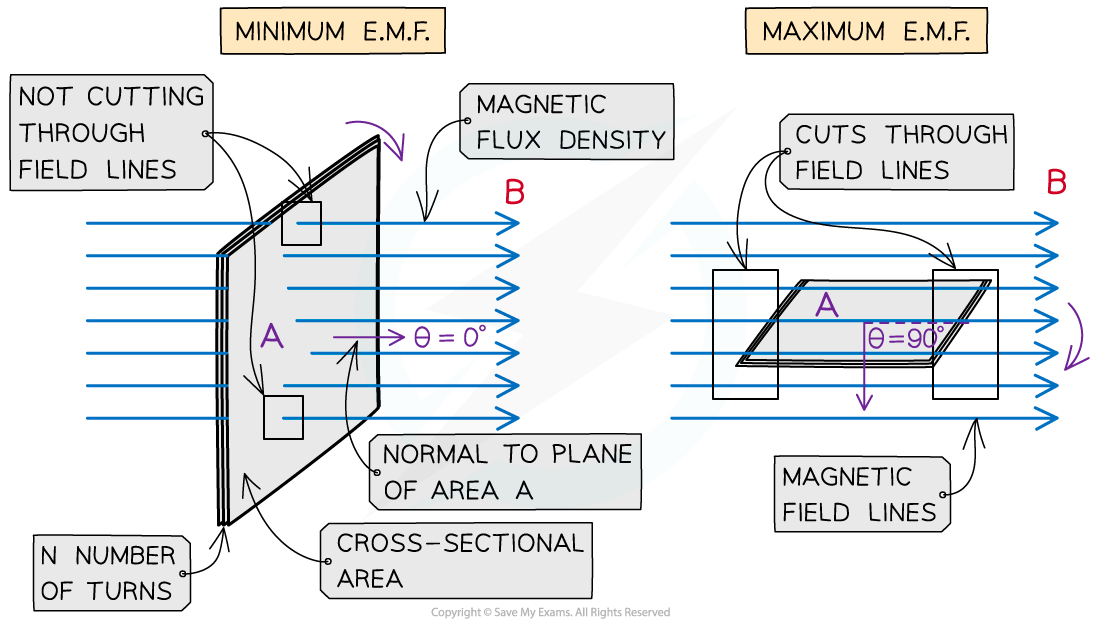
When a coil is completely vertical relative to the magnetic field lines:
The magnetic flux linkage is at a maximum - the field lines are travelling through the area of the coil
There is no e.m.f induced - there is no cutting of field lines i.e. there is no change in magnetic flux linkage
When a coil is completely horizontal relative to the magnetic field lines:
The magnetic flux linkage is zero - there are no field lines travelling through the area of the coil
Maximum e.m.f is induced - this is when the coil is cutting the magnetic field lines at the greatest rate, i.e. the maximum rate of change of magnetic flux linkage
e.m.f. induced and the rotation of a coil
Worked Example
A small rectangular coil contains 350 turns of wire. The longer sides are 3.5 cm, and the shorter sides are 1.4 cm.
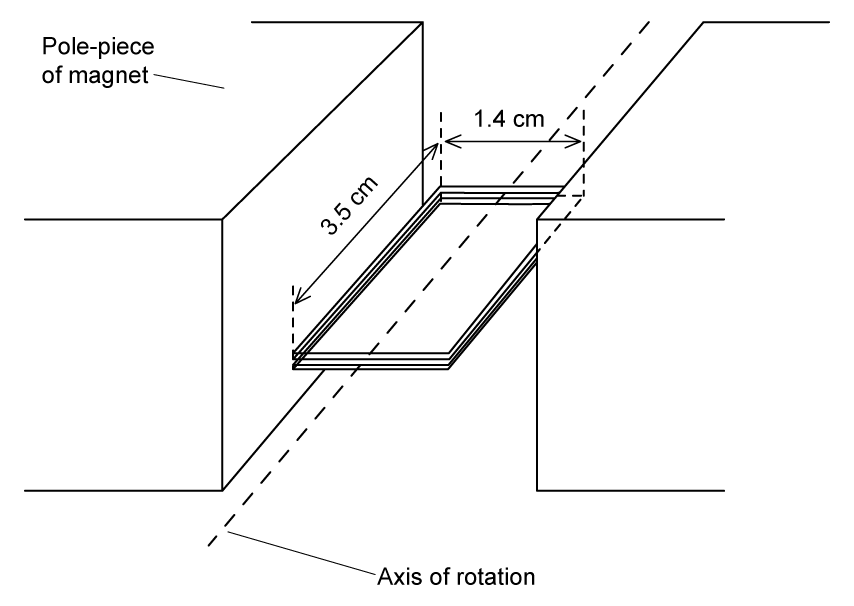
The coil is held between the poles of a large magnet so that the coil can rotate about an axis through its centre. The magnet produces a uniform magnetic field of flux density 80 mT between its poles.
The coil is positioned horizontally and then turned through an angle of 40° over a time interval of 0.18 s.
Calculate the magnitude of the average e.m.f induced in the coil.
Answer:
Step 1: Write down the known quantities
Magnetic flux density, B = 80 mT = 80 × 10-3 T
Area, A = 3.5 × 1.4 = (3.5 × 10-2) × (1.4 × 10-2) = 4.9 × 10-4 m2
Number of turns, N = 350
Angle of rotation, θ = 40°
Time interval, Δt = 0.18 s
Step 2: Write down the equation for Faraday’s law:
Step 3: Write out the equation for the change in flux linkage:
The number of turns N and the coil area A stay constant
The flux through the coil changes as B cos θ as it rotates
Therefore, the equation to use is:
Step 4: Determine the change in magnetic flux linkage
The coil is initially horizontal, so the plane of the area is parallel to the magnetic field, so
The initial flux linkage through the coil is:
The coil rotates through 40°, so the angle between the plane of the area and the field is
The final flux linkage through the coil is:
Therefore, the change in flux linkage is:
Step 5: Substitute the change in flux linkage and time into Faraday’s law equation:
Examiner Tips and Tricks
The important point to notice is that an emf is induced in a conductor in a magnetic field if there is change in flux linkage. This means the conductor (e.g. a coil) must cut through the field lines to have an emf (and hence a current) induced.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?