Potential Energy Calculations

Electric Potential Energy of Two Point Charges

The electric potential energy E_p at point in an electric field is defined as:

The work done in bringing a charge from infinity to that point

The electric potential energy of a pair of point charges Q₁and Q₂ is defined by:

$E_{p} = \frac{Q_{1} \times Q_{2}}{4 \times π \times ε_{0} \times r}$

Where:

E_p = electric potential energy (J)
r = separation of the charges Q₁ and Q₂ (m)
ε₀ = permittivity of free space (F m^-1)

The potential energy equation is defined by the work done in moving point charge Q₂ from infinity towards a point charge Q₁.

The work done is equal to:

W = q \times Δ V_{e}

- Where:
  - W = work done (J)
  - V = electric potential due to a point charge (V)
  - Q = Charge producing the potential (C)

This equation is relevant to calculate the work done due on a charge in a uniform field
- Unlike the electric potential, the potential energy will always be positive
- Recall that at infinity, V = 0 therefore E_p = 0

It is more useful to find the change in potential energy, for example, as one charge moves away from another

- The change in potential energy from a charge Q₁ at a distance r₁ from the centre of charge Q₂ to a distance r₂ is equal to:

Δ E_{p} = \frac{Q_{1} \times Q_{2}}{4 \times π \times ε_{0}} \times (\frac{1}{r_{1}} - \frac{1}{r_{2}})

- The change in electric potential ΔV is the same, without the charge Q₂

Δ V = \frac{Q}{4 \times π \times ε_{0}} \times (\frac{1}{r_{1}} - \frac{1}{r_{2}})

There is another similarity with gravitational potential, as both equations are very similar to the change in gravitational potential between two points near a point mass

Worked example

An $α$ -particle ${}_{2}^{4}H e$ is moving directly towards a stationary gold nucleus ${}_{79}^{197}A u$ .

At a distance of 4.7 × 10^-15 m, the $α$ -particle momentarily comes to rest.

Calculate the electric potential energy of the particles at this instant.

Step 1: Write down the known quantities

- Distance, r = 4.7 × 10^-15 m
- The charge of one proton, q = +1.60 × 10^-19 C

An alpha particle (Helium nucleus) has 2 protons

- Charge of alpha particle, Q₁ = 2 × 1.60 × 10^-19 = +3.2 × 10^-19 C

The gold nucleus has 79 protons

- Charge of gold nucleus, Q₂ = 79 × 1.60 × 10^-19 = +1.264 × 10^-17 C

Step 2: Write down the equation for electric potential energy

E_{p} = \frac{Q_{1} \times Q_{2}}{4 \times π \times ε_{0} \times r}

Step 3: Substitute values into the equation

E_{p} = \frac{(3.2 \times 10^{- 19}) \times (1.264 \times 10^{- 17})}{(4 π \times 8.85 \times 10^{- 12}) \times (4.7 \times 10^{- 15})} = 7.7 \times 10^{- 12} J

Gravitational Potential Energy Between Two Point Masses

The gravitational potential energy (G.P.E) at point in a gravitational field is defined as:

The work done in bringing a mass from infinity to that point

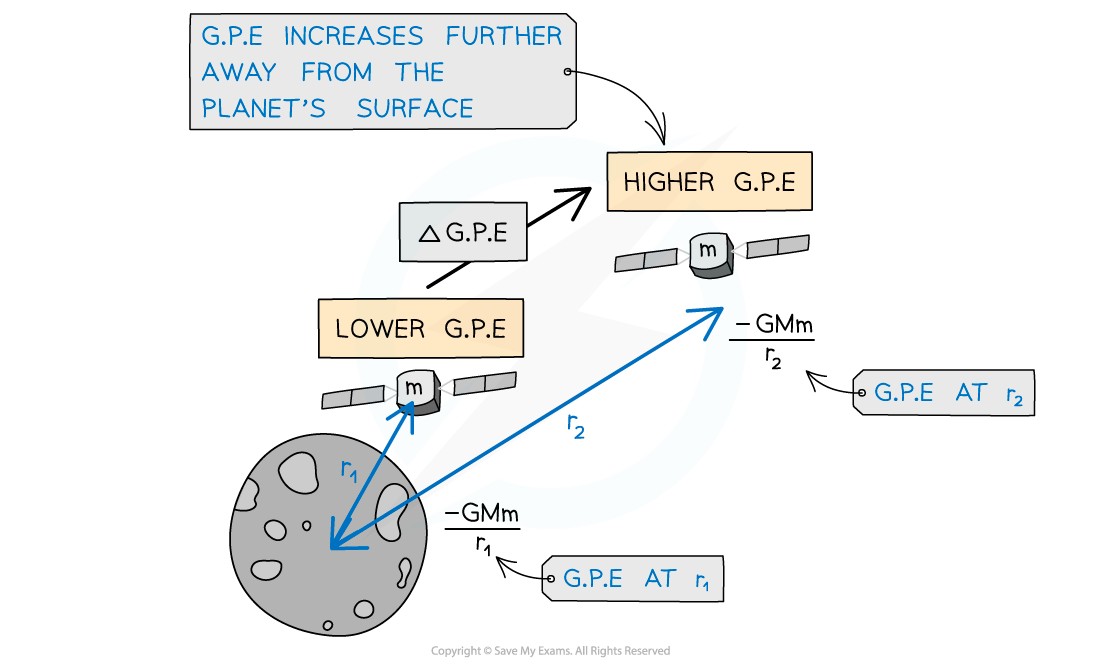
The equation for G.P.E of two point masses m and M at a distance r is:

G . P . E = - \frac{G \times M \times m}{r}

G.P.E is calculated using mgh, but recall that at infinity, g = 0 and therefore G.P.E = 0

GPE equation, downloadable AS & A Level Physics revision notes

It is more useful to find the change in G.P.E for example for a satellite which is lifted into space from the Earth’s surface

- The change in G.P.E from for an object of mass m at a distance r₁ from the centre of mass M, to a distance of r₂ further away is:

Δ G . P . E = - \frac{G \times M \times m}{r_{2}} - (- \frac{G \times M \times m}{r_{1}}) = G \times M \times m \times (\frac{1}{r_{1}} - \frac{1}{r_{2}})

Change in gravitational potential energy between two points

- The change in potential Δg is the same, without the mass of the object m:

Δ g = - \frac{G \times M}{r_{2}} - (- \frac{G \times M}{r_{1}}) = G \times M \times (\frac{1}{r_{1}} - \frac{1}{r_{2}})

Change in gravitational potential between two points

Change in GPE, downloadable AS & A Level Physics revision notes

Gravitational potential energy increases as a satellite leaves the surface of the Moon

Worked example

Calculate the difference in potential energy when a satellite of mass 1450 kg when it is moved from a distant orbit of 980 km above Earth’s surface to a closer orbit of 480 km above the Earth’s surface. Assume the Earth’s mass to be 5.97 x 10²⁴ kg and the radius of the Earth to be 6.38 x 10⁶ m.

Step 1: Write down the known quantities

- Initial distance of orbit above Earth’s surface: 980 km
- Final distance of orbit above Earth’s surface: 480 km
- Mass of the satellite: m = 1450 kg
- Earth’s mass: M = 5.97 x 10²⁴kg
- Radius of the Earth: 6.38 x 10⁶ m

Step 2: Write down the equation for change in gravitational potential energy

$Δ G . P . E = - \frac{G \times M \times m}{r_{2}} - (- \frac{G \times M \times m}{r_{1}}) = G \times M \times m \times (\frac{1}{r_{1}} - \frac{1}{r_{2}})$

Step 3: Convert distances into standard units and include Earth radius

- Distance from centre of Earth to orbit 1:

9.8 x 10⁵ m + 6.38 x 10⁶ m = 7.36 x 10⁶ m

- Distance from centre of Earth to orbit 2:

4.8 x 10⁵ m + 6.38 x 10⁶ m = 6.86 x 10⁶ m

Step 4: Substitute values into the equation

Δ G . P . E = 6.67 \times 10^{- 11} \times 5.97 \times 10^{24} \times 1450 \times (\frac{1}{7.36 \times 10^{6}} - \frac{1}{6.86 \times 10^{6}}) = 5.72 \times 10^{9} J

Step 5: State final answer

- The difference in gravitational potential energy between the two orbits is: 5.72 x 10⁹ J

Potential Energy Calculations (DP IB Physics: HL)

Revision Note