Gravitational Field Strength (DP IB Physics): Revision Note
Gravitational Field Strength
There is a universal force of attraction between all matter with mass
This force is known as the ‘force due to gravity’ or the weight
The Earth’s gravitational field is responsible for the weight of all objects on Earth
A gravitational field is defined as:
A region of space where a test mass experiences a force due to the gravitational attraction of another mass
The direction of the gravitational field always acts toward the centre of the mass which produces the field
This is because gravitational forces are always attractive
Gravity has an infinite range, meaning it affects all objects in the universe
There is a greater gravitational force around objects with a large mass (such as planets)
There is a smaller gravitational force around objects with a small mass (almost negligible for atoms)

The Earth's gravitational field produces an attractive force. The force of gravity is always attractive
The gravitational field strength at a point is defined as:
The force per unit mass experienced by a test mass at that point
This can be written in equation form as:
Where:
g = gravitational field strength (N kg−1)
F = force due to gravity, or weight (N)
m = mass of test mass in the field (kg)
This equation shows that:
On planets with a large value of g, the gravitational force per unit mass is greater than on planets with a smaller value of g
An object's mass remains the same at all points in space
However, on planets such as Jupiter, the weight of an object will be greater than on a less massive planet, such as Earth
This means the gravitational force would be so high that humans, for example, would not be able to fully stand up
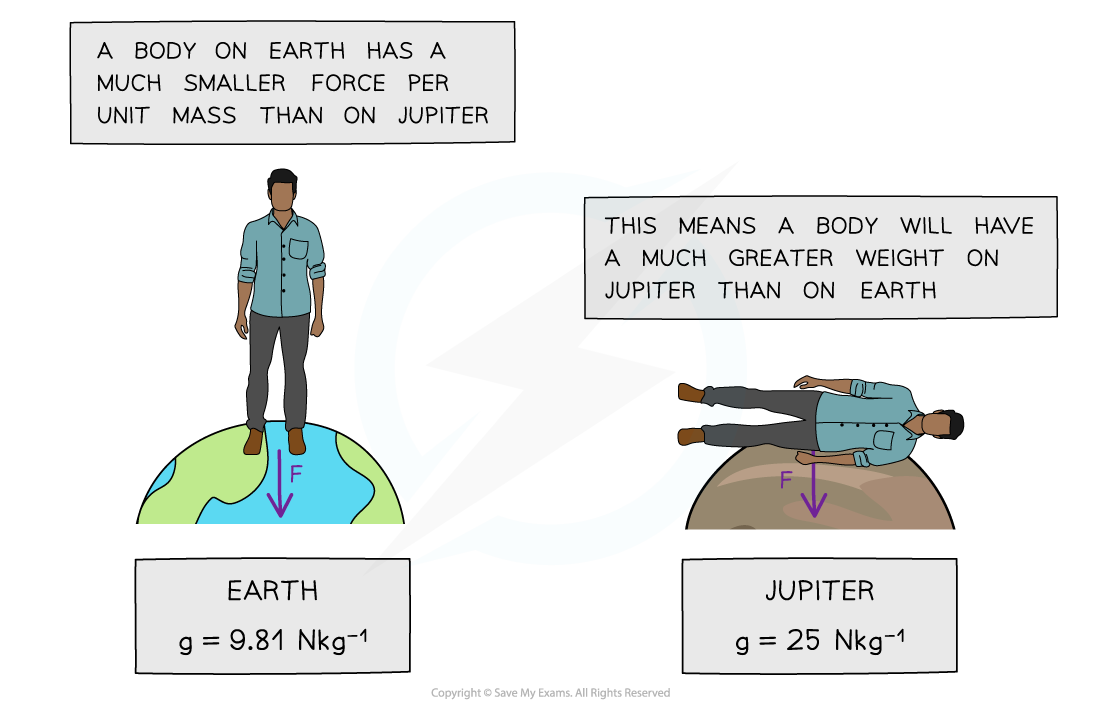
A person’s weight on Jupiter would be so large that a human would be unable to fully stand up
Factors that affect the gravitational field strength at the surface of a planet are:
the radius r (or diameter) of the planet
the mass M (or density) of the planet
This can be shown by equating the equation F = mg with Newton's law of gravitation:
Substituting the force F with the gravitational force mg leads to:
Cancelling the mass of the test mass m leads to the equation:
Where:
G = Newton's Gravitational Constant
M = mass of the body causing the field (kg)
r = distance from the mass where you are calculating the field strength (m)
This equation shows that:
The gravitational field strength g depends only on the mass of the body M which produces the field
Hence, objects with any mass m in that field will experience the same gravitational field strength
The gravitational field strength g is inversely proportional to the square of the radial distance, r2
Worked Example
Calculate the mass of an object with a weight of 10 N on Earth.
Answer:

Worked Example
The mean density of the Moon is times the mean density of the Earth. The gravitational field strength on the Moon is
the gravitational field strength on Earth.
Determine the ratio of the Moon's radius to the Earth's radius
.
Answer:
Step 1: Write down the known quantities
= gravitational field strength on the Moon,
= mean density of the Moon
= gravitational field strength on the Earth,
= mean density of the Earth
Step 2: Write down the equations for the gravitational field strength, volume and density
Gravitational field strength:
Volume of a sphere:
Density:
Step 3: Substitute the relationship between M and r into the equation for g
Step 4: Find the ratio of the gravitational field strength
Step 5: Substitute the ratio of the densities into the equation
Step 6: Calculate the ratio of the radii
Examiner Tips and Tricks
There is a big difference between g and G (sometimes referred to as ‘little g’ and ‘big G’ respectively), g is the gravitational field strength and G is Newton’s gravitational constant. Make sure not to use these interchangeably!
Remember the equation , which may come in handy with some calculations. The equation for the volume of common shapes is in your data booklet.

Unlock more, it's free!
Did this page help you?