Combining & Resolving Vectors (DP IB Physics): Revision Note
Combining & resolving vectors
Vectors can be changed in a variety of ways, such as
combining through vector addition or subtraction
combining through vector multiplication
resolving into components through trigonometry
Combining vectors
Vectors can be combined by adding or subtracting them to produce the resultant vector
The resultant vector is sometimes known as the ‘net’ vector (e.g. the net force)
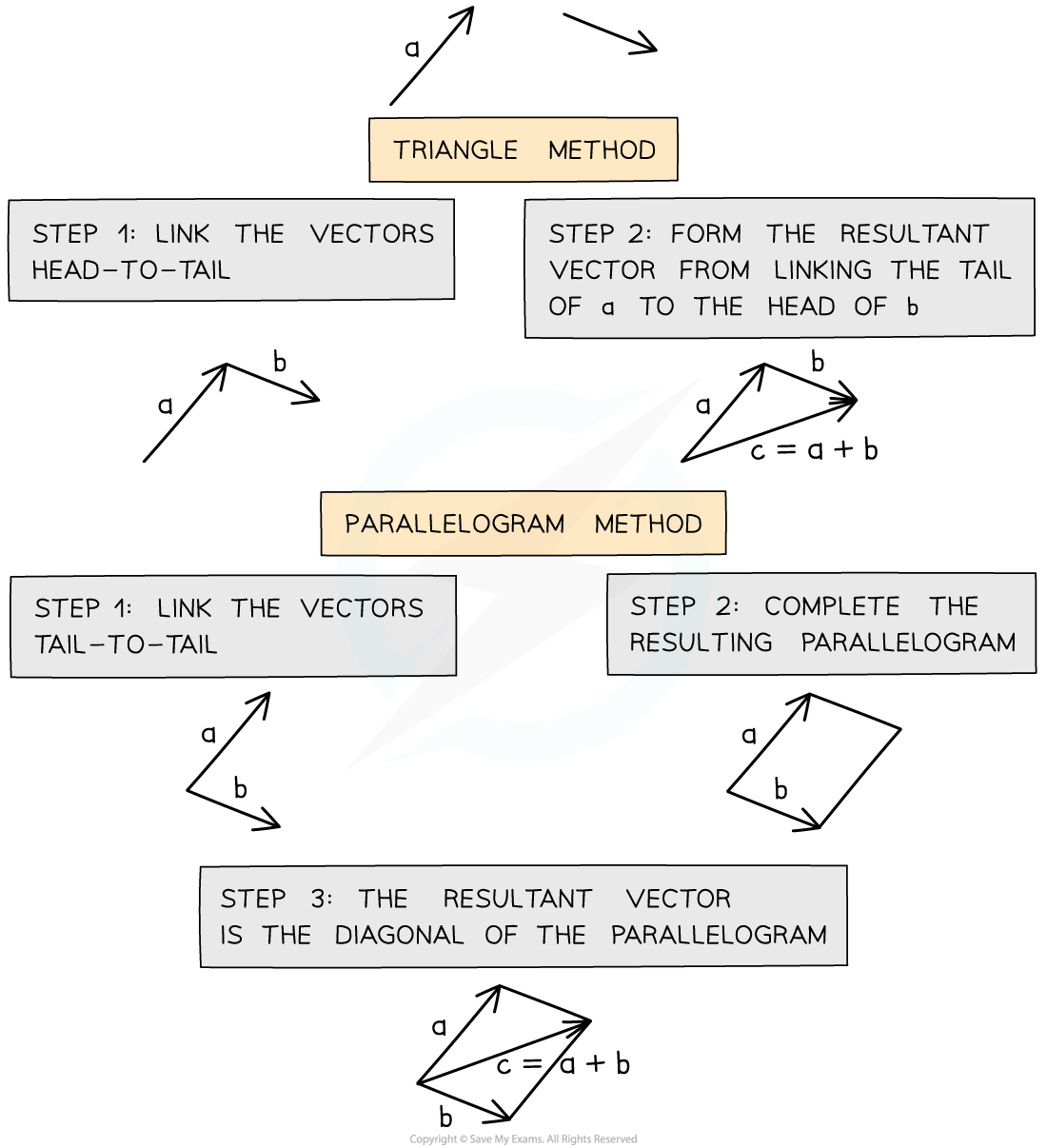
There are two methods that can be used to combine vectors: the triangle method and the parallelogram method
Triangle method
To combine vectors using the triangle method:
Step 1: link the vectors head-to-tail
Step 2: the resultant vector is formed by connecting the tail of the first vector to the head of the second vector
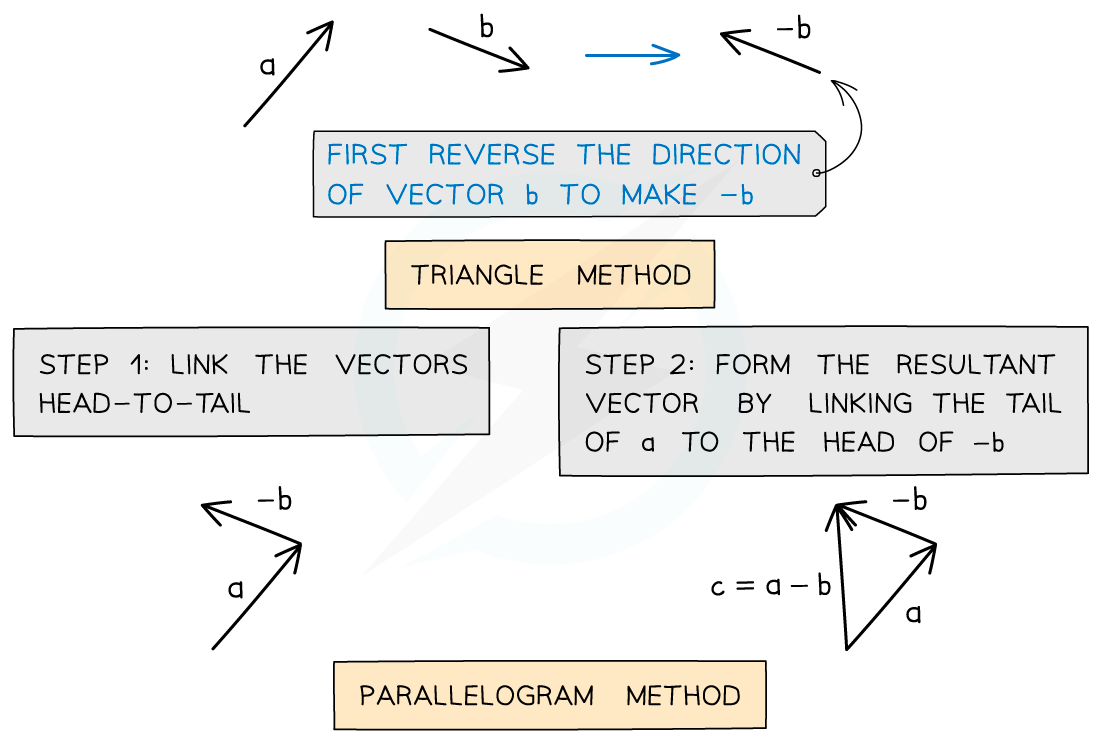
To subtract vectors, change the direction of the vector from positive to negative and add them in the same way

The triangle method links vectors tip to tail to find the resultant vector
Parallelogram method
To combine vectors using the parallelogram method:
Step 1: link the vectors tail-to-tail
Step 2: complete the resulting parallelogram
Step 3: the resultant vector is the diagonal of the parallelogram

The parallelogram method links vectors tail to tail to find the resultant vector
When two or more vectors are added together (or one is subtracted from the other), a single vector is formed, known as the resultant vector
The magnitude of the resultant vector can be found using Pythagoras' theorem or trigonometry
Worked Example
Draw the vector c = a + b.
Answer:
Worked Example
Draw the vector c = a – b.
Answer:
Vector multiplication
The product of a scalar and a vector is always a vector
For example, consider the scalar quantity mass
and the vector quantity acceleration
The product of mass
and acceleration
gives rise to a vector quantity force
For another example, consider the scalar quantity mass
and the vector quantity velocity
The product of mass
and velocity
gives rise to a vector quantity momentum
Resolving vectors
Two vectors can be represented by a single resultant vector
Resolving a vector is the opposite of adding vectors
A single resultant vector can be resolved
This means it can be represented by two vectors, which in combination, have the same effect as the original one
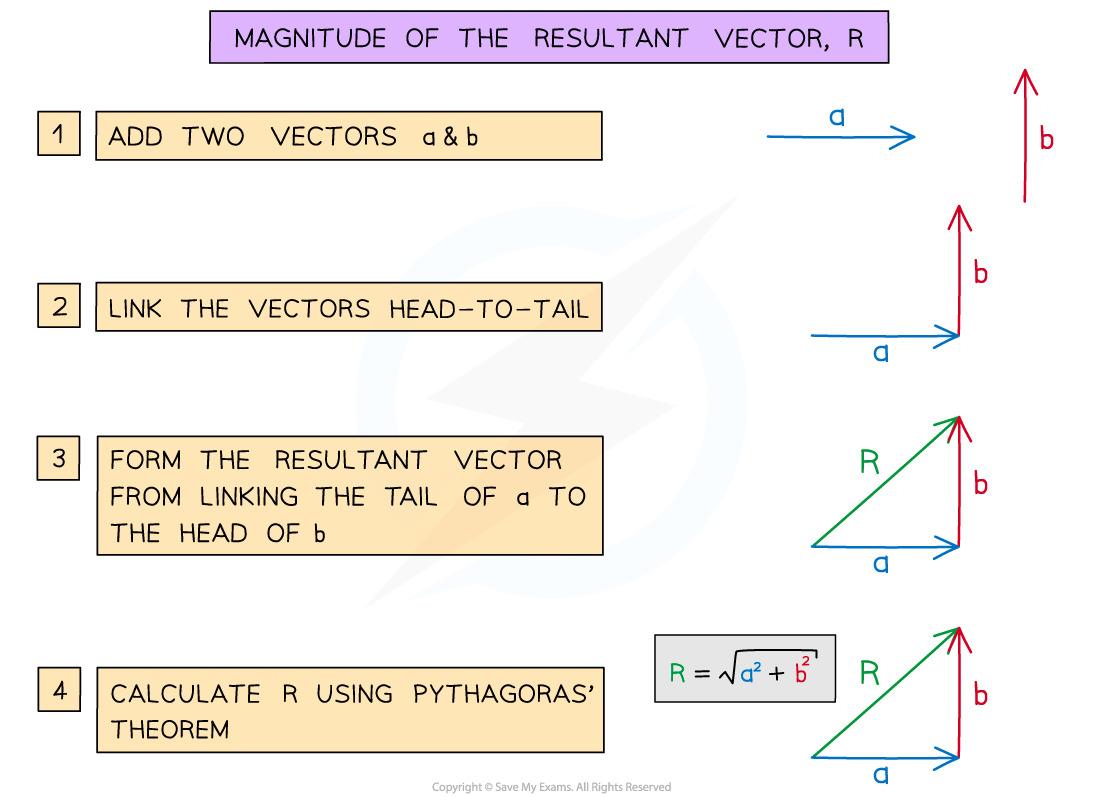
The magnitude of the resultant vector is found by using Pythagoras’ Theorem
When a single resultant vector is broken down into its parts, those parts are called components
For example, a force vector of magnitude FR and an angle of θ to the horizontal is shown below

Resolving two force vectors F1 and F2 into a resultant force vector FR
It is possible to resolve this vector into its horizontal and vertical components using trigonometry

The resultant force FR can be split into its horizontal and vertical components
The direction of the resultant vector is found from the angle it makes with the horizontal or vertical
The question should imply which angle it is referring to (i.e. calculate the angle from the x-axis)
Calculating the angle of this resultant vector from the horizontal or vertical can be done using trigonometry
Either the sine, cosine or tangent formula can be used depending on which vector magnitudes are calculated
For the horizontal component, Fx = F cos θ
For the vertical component, Fy = F sin θ
Worked Example
A hiker walks a distance of 6 km due east and 10 km due north.
Calculate the magnitude of their displacement and its direction from the horizontal.
Answer:
Step 1: Draw a vector diagram
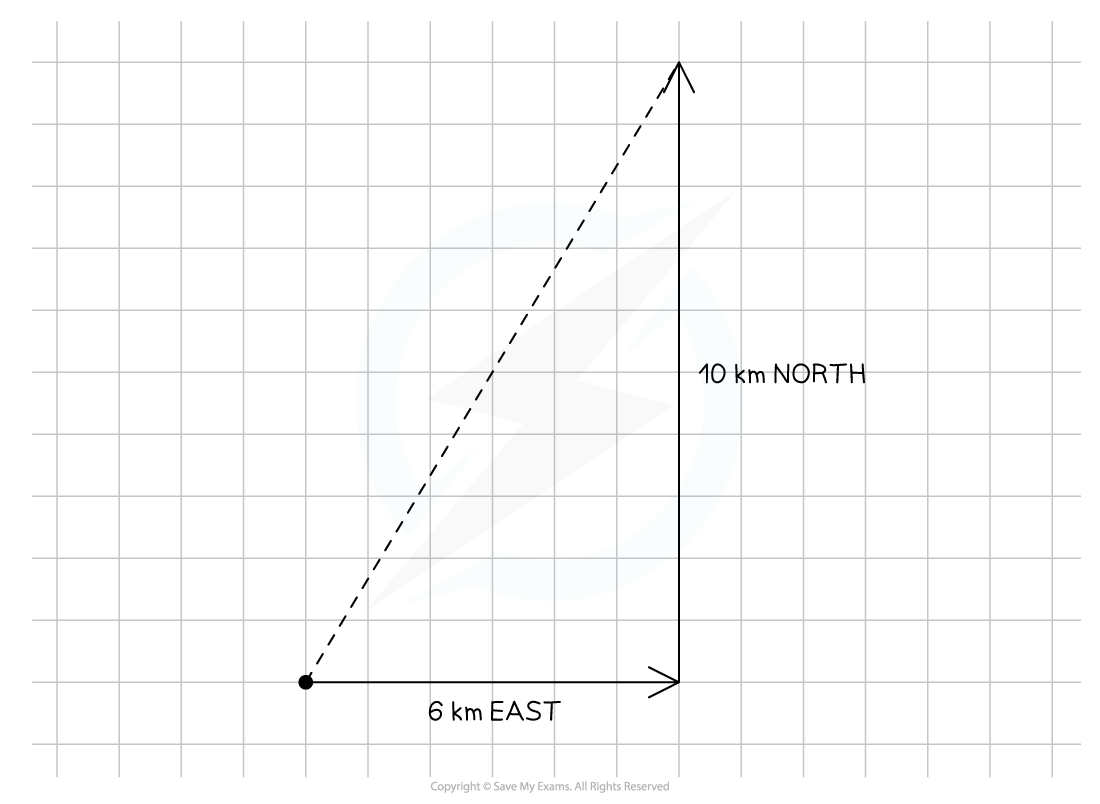
Step 2: Calculate the magnitude of the resultant vector using Pythagoras' Theorem
Resultant vector = 11.66
Step 3: Calculate the direction of the resultant vector using trigonometry
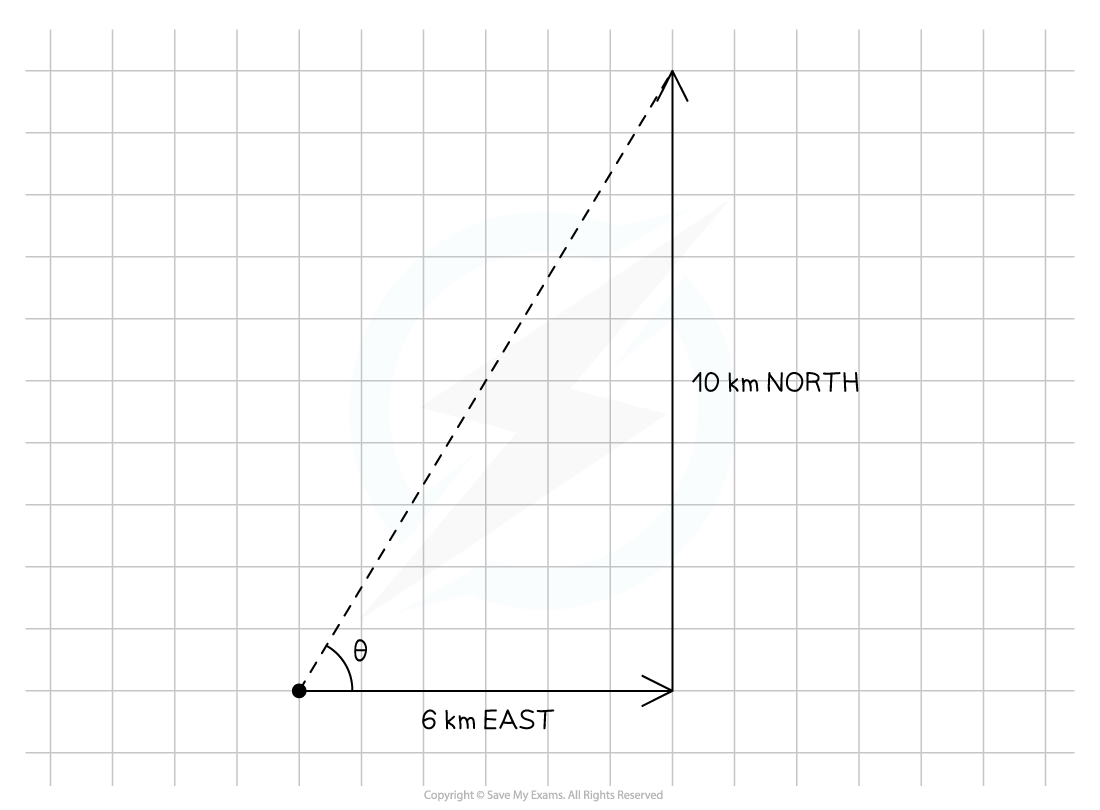
Step 4: State the final answer complete with direction
Vector magnitude: 12 km
Direction: 59° east and upwards from the horizontal
Examiner Tips and Tricks
Make sure you are confident using trigonometry as it is used a lot in vector calculations!
If you're unsure as to which component of the force is cos θ or sin θ, just remember that the cos θ is always the adjacent side of the right-angled triangle


Unlock more, it's free!
Did this page help you?