IBPhysicsSLRevision NotesWave BehaviourWave PhenomenaRefraction of Waves

Syllabus Edition

First teaching 2023

First exams 2025

|

Refraction of Waves (SL IB Physics)

Revision Note

Test yourselfFlashcards
Ashika

Author

Ashika

Last updated

Snell's Law

  • Snell’s law relates the angle of incidence to the angle of refraction at a boundary between two media

Refractive Index

  • The refractive index, n of a material tells us how optically dense it is
  • The refractive index of air is n = 1
    • Media that are more optically dense than air will have a refractive index of n > 1
    • Media that are less optically dense than air will have a refractive index of n < 1
  • The higher the refractive index of a material then the more optically dense and hence the slower light will travel through it
  • The refractive index of a material is calculated using the equation: 

n space equals space c over v

  • Where:
    • n = absolute refractive index of the medium
    • c = speed of light in a vacuum in metres per second (m s–1), 3.00 × 108 m s–1, as given in the data booklet
    • v = speed of light in the medium in metres per second (m s–1)

  • Note that, being a ratio, the absolute refractive index is a dimensionless quantity
    • This means that it has no units

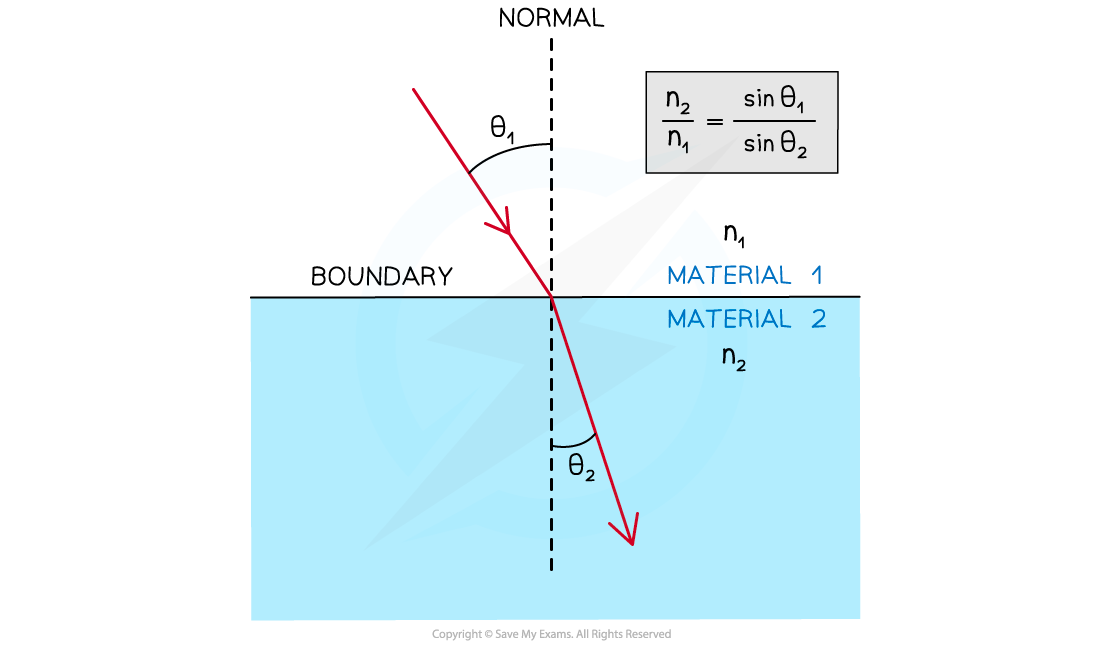
Snell's Law

  • Snell’s law is given by:

n subscript 1 over n subscript 2 space equals space fraction numerator sin space theta subscript 2 over denominator sin space theta subscript 1 end fraction space equals space v subscript 2 over v subscript 1

  • Where:
    • n1 = the refractive index of material 1
    • n2 = the refractive index of material 2
    • θ1 = the angle of incidence of the ray in material 1
    • θ2 = the angle of refraction of the ray in material 2
    • v1 = the speed of the wave in material 1
    • v2 = the speed of the wave in material 2
  • Snell's Law describes the angle at which light meets the boundary and the angle at which light leaves the boundary, so that the light travels through the media in the least amount of time

  • Light can travel through medium 1 at a speed of v1 due to the optical density n1 of that medium
    • Light will approach the boundary at angle θ1
    • This is the angle of incidence
  • Light can travel through medium 2 at a speed of v2 due to the optical density n2 of that medium
    • Light will leave the boundary at angle θ2
    • This is the angle of refraction

Snell’s Law

Snell's Law

  • Snell's Law can also be given in a more convenient form:

n subscript 1 space sin space theta subscript 1 space equals space n subscript 2 space sin space theta subscript 2

Worked example

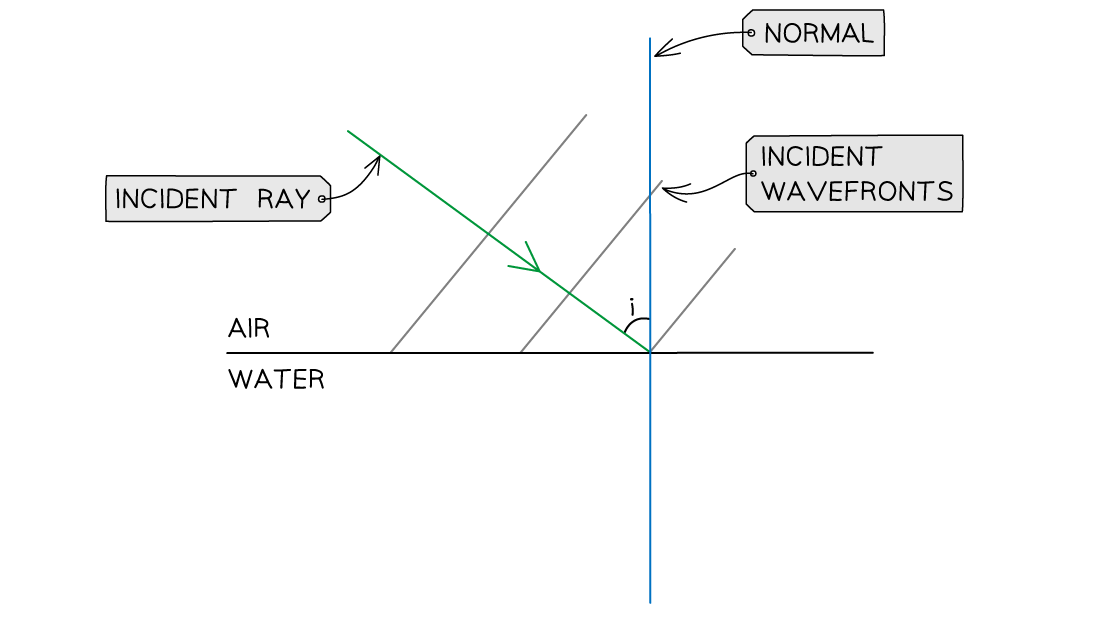
Wavefronts travel from air to water as shown. Add the refracted wavefronts to the diagram.

4-4-3-we-refraction-question



Answer:

Step 1: Add the incident ray to mark the direction of the incident waves 

  • The incident ray must be perpendicular to all wavefronts
  • Remember to add an arrow pointing towards the air-water boundary


4-4-3-we-refraction-answer-step-1

Step 2: Add the normal at the point of incidence 

  • Mark the angle of incidence (i) between the normal and the incident ray


4-4-3-we-refraction-answer-step-2

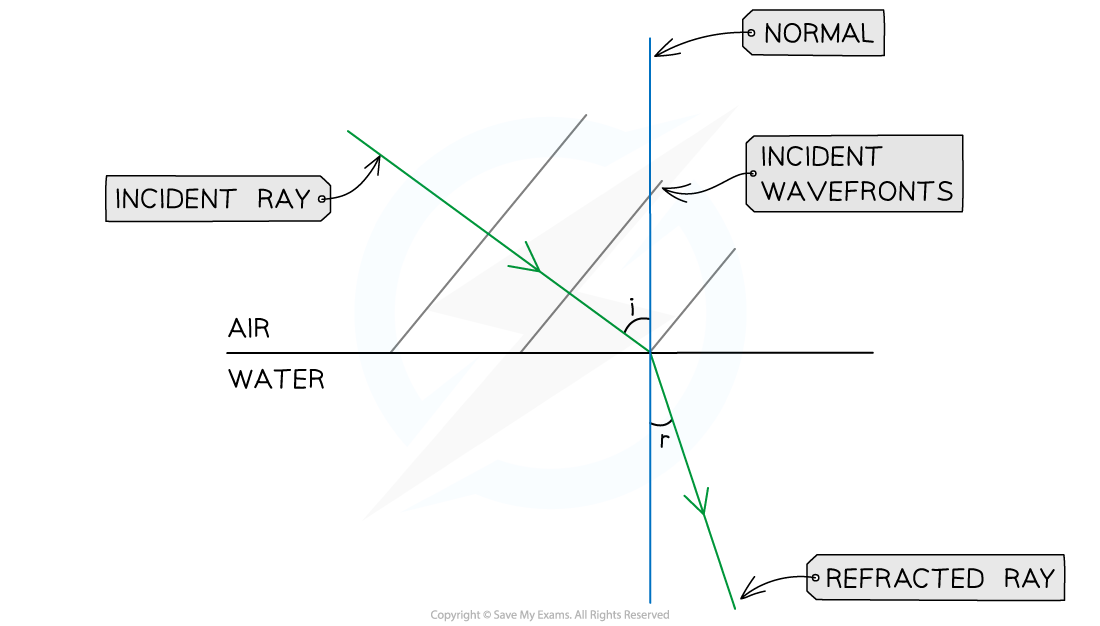
Step 3: Draw the refracted ray into the water 

  • Water is optically denser than air
  • The refracted ray must bend towards the normal
  • Mark the angle of refraction (r) between the normal and the refracted ray
  • By eye, i > r


4-4-3-we-refraction-answer-step-3

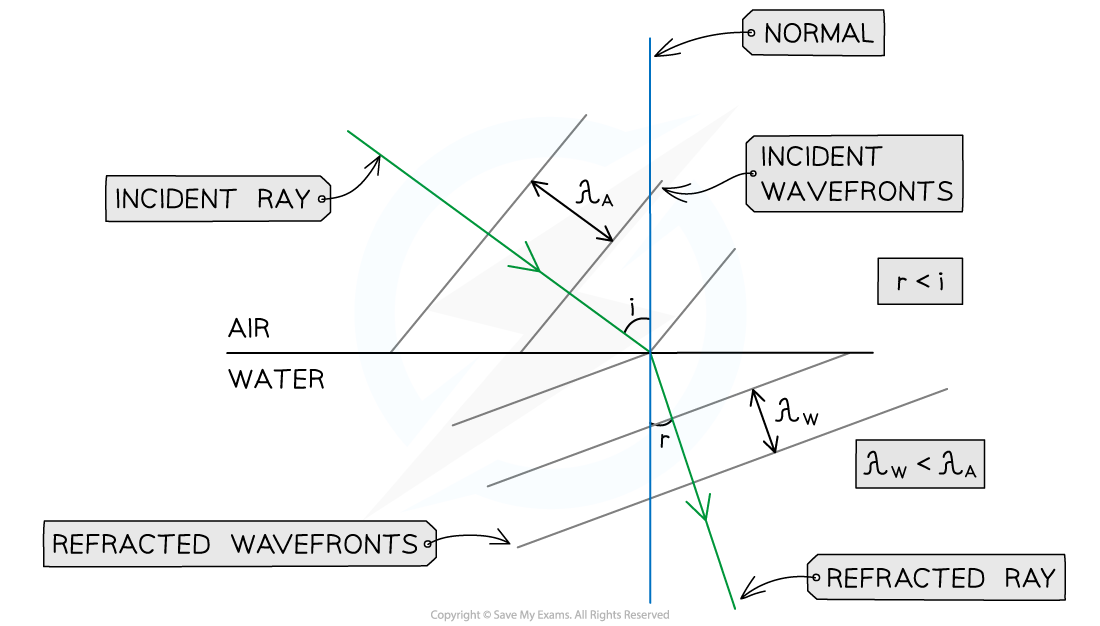
Step 4: Add three equally spaced wavefronts, all perpendicular to the refracted ray 

  • The refracted wavefronts must be closer to each other than the incident wavefronts, since:
    • The speed v of the waves decreases in water
    • The frequency f of the waves stays the same
    • The wavelength λ of the waves in water is shorter than the wavelength of the waves in air λW < λA, since v = fλ


4-4-3-we-refraction-answer-step-4

Worked example

Light travels from air into glass. Determine the speed of light in glass.

  • Refractive index of air, n1 = 1.00
  • Refractive index of glass, n2 = 1.50



Answer:

Step 1: Write down the known quantities 

  • n1 = 1.00
  • n2 = 1.50
  • From the data booklet, c = 3 × 108 m s–1 (speed of light in air)

Step 2: Write down the relationship between the refractive indices of air and glass and the speeds of light in air (v1) and glass (v2)

Step 3: Rearrange the above equation to calculate v2

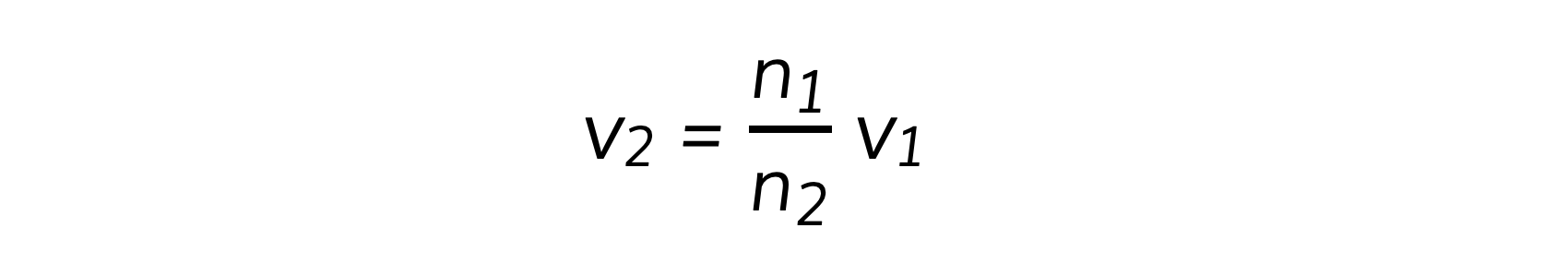
Step 4: Substitute the numbers into the above equation 

v2 = 2 × 108 m s–1

Worked example

A light ray is directed at a vertical face of a glass cube. The angle of incidence at the vertical face is 39° and the angle of refraction is 25° as shown in the diagram.

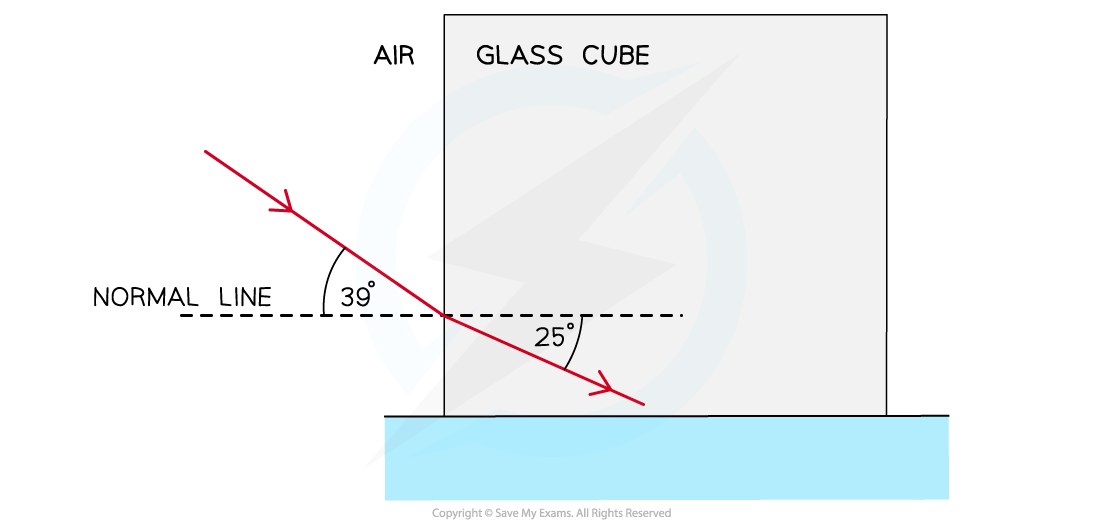
Snell’s Law Worked Example, downloadable AS & A Level Physics revision notes

Show that the refractive index of the glass is about 1.5.



Answer:

Examiner Tip

Always double-check if your calculations for the refractive index are greater than 1. Otherwise, something has definitely gone wrong in your calculation! The refractive index of air might not be given in the question. Always assume that nair = 1

Make sure your calculator is always in degrees mode for calculating the sine of angles!

Always check that the angle of incidence and refraction are the angles between the normal and the light ray. If the angle between the light ray and the boundary is calculated instead, calculate 90 – θ (since the normal is perpendicular to the boundary) to get the correct angle

Critical Angle & Total Internal Reflection (TIR)

  • As the angle of incidence (i) is increased, the angle of refraction (r) also increases until it gets closer to 90°
  • When the angle of refraction is exactly 90° the light is refracted along the boundary between the two material
    • At this point, the angle of incidence is known as the critical angle θc

Critical Angle

  • The larger the refractive index of a material, the smaller the critical angle

  • When light is shone at a boundary between two materials, different angles of incidence result in different angles of refraction

    • As the angle of incidence is increased, the angle of refraction also increases

    • Until the angle of incidence reaches the critical angle

  • When the angle of incidence = critical angle then:

    • Angle of refraction = 90°

    • The refracted ray is refracted along the boundary between the two materials

  • When the angle of incidence < critical angle then:

    • the ray is refracted and exits the material

  • When the angle of incidence > critical angle then:

    • the ray undergoes total internal reflection

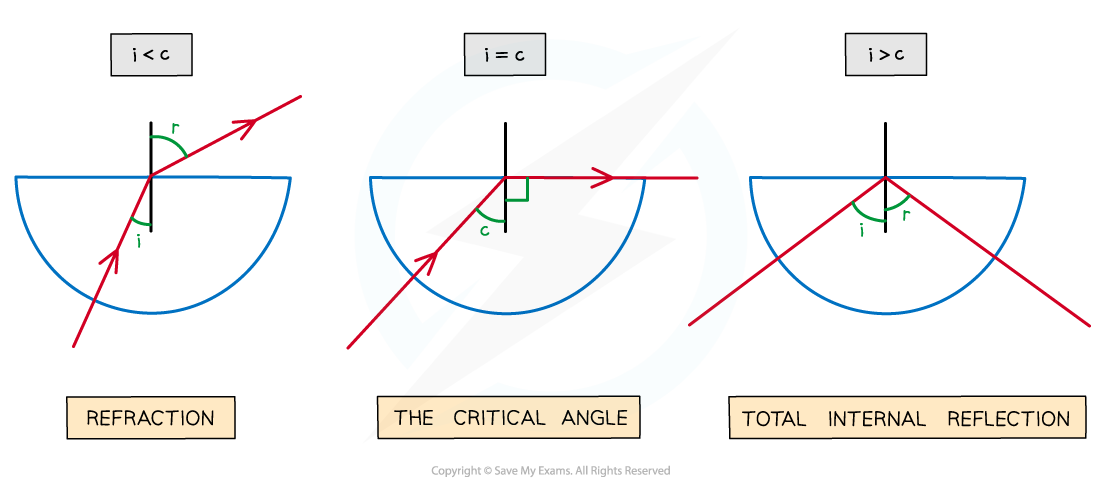
Total internal reflection, IGCSE & GCSE Physics revision notes

As the angle of incidence increases it will eventually exceed the critical angle and lead to the total internal reflection of the light

Critical Angle Equation

  • The critical angle of material 1 is found using the equation:

sin space theta subscript c space equals space n subscript 2 over n subscript 1

  • Where:
    • θc = critical angle of material 1 (°)
    • n1 = absolute refractive index of material 1
    • n2 = absolute refractive index of material 2

  • The two conditions for total internal reflection to occur are:
    • The refractive index of the second medium must be less than the refractive index of the first, n2 < n1
    • The angle of incidence must be greater than the critical angle, θi > θc

Total Internal Reflection

  • Total internal reflection is a special case of refraction that occurs when:

    • The angle of incidence within the denser medium is greater than the critical angle (I > θc)

    • The incident refractive index n1 is greater than the refractive index of the material at the boundary n2 (n1 > n2)

  • Total internal reflection follows the law of reflection

angle of incidence = angle of reflection

  • A denser medium has a higher refractive index

    • For example, the refractive index of glass, ng > the refractive index of air, na

  • Light rays inside a material with a higher refractive index are more likely to be totally internally reflected

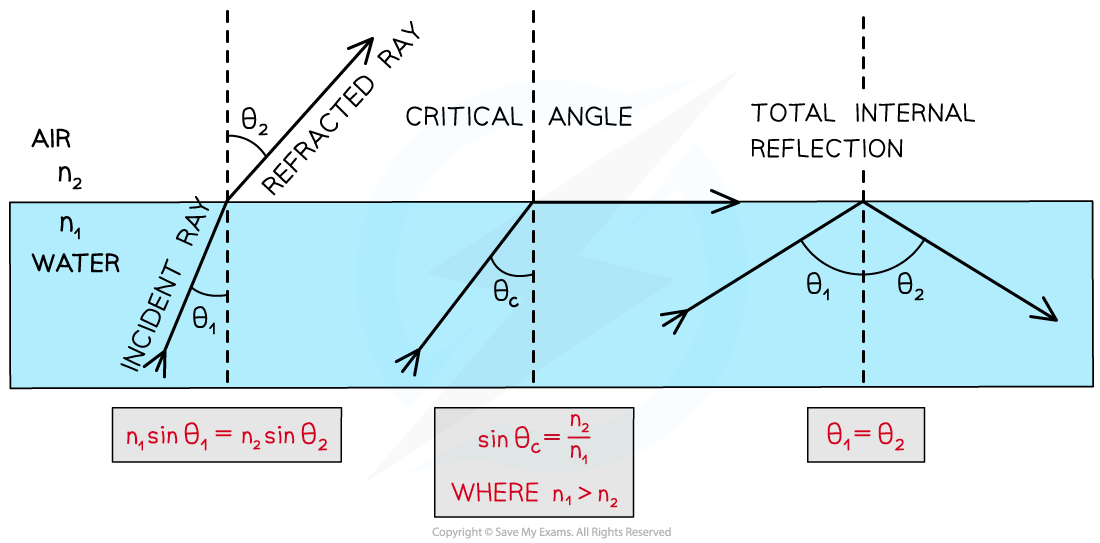
Total Internal Reflection, downloadable AS & A Level Physics revision notes

Angles of incidence, reflection and refraction to satisfy the conditions for total internal reflection

Worked example

Light travels from a material with refractive index 1.2 into air.

Determine the critical angle of the material.

Answer:

Step 1: Write down the known quantities 

  • Refractive index of material 1, n1 = 1.2
  • Refractive index of air, n2 = 1.0

Step 2: Write down the equation for the critical angle θc

Step 3: Substitute the numbers into the above equation 

sinθc = 0.83

Step 4: Calculate θc by taking sin–1 of the above equation 

θc = sin–1 0.83

θc = 56°

Examiner Tip

You do not need to remember the derivation for the critical angle, but you must understand and remember the critical angle formula, as this is not given in your data booklet. 

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Diffraction of WavesNext:Superposition of Waves
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.