Time Period of a Simple Pendulum (SL IB Physics)

• A simple pendulum consists of a string and a bob at the end
  • The bob is a weight, generally spherical and considered a point mass
  • The bob moves from side to side
  • The string is light and inextensible remaining in tension throughout the oscillations
  • The string is attached to a fixed point above the equilibrium position

• The time period of a simple pendulum for small angles of oscillation is given by:

• Where:
  • T = time period (s)
  • L = length of string (from the pivot to the centre of mass of the bob) (m)
  • g = gravitational field strength (N kg^-1)

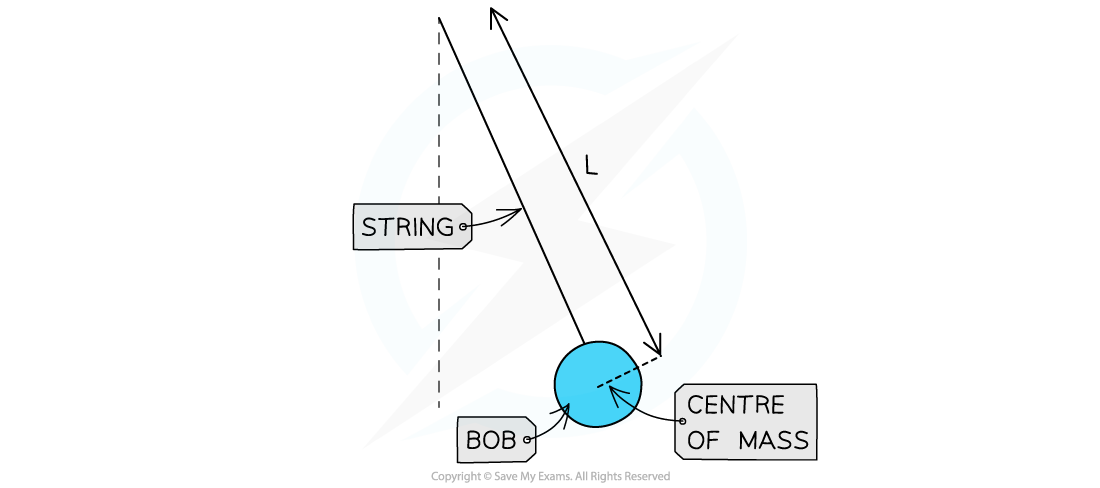
A simple pendulum

• The time period of a pendulum depends on gravitational field strength
  • Therefore, the time for a pendulum to complete one oscillation would be different on the Earth and the Moon

Small Angle Approximation

• This formula for time period is limited to small angles (θ < 10°) and therefore small amplitudes of oscillation from the equilibrium point
• The restoring force of a pendulum is equal to the component of weight acting along the arc of the circle towards the equilibrium position
  
  • It is assumed to act at an angle θ to the horizontal
  • Using the small angle approximation: sin θ ≅ θ 

Forces on a pendulum when it is displaced. Assuming θ < 10°, the small angle approximation can be used to describe the time period of a simple pendulum