Stoke's Law (SL IB Physics)

Viscous Drag

• Viscous drag is defined as:

the frictional force between an object and a fluid which opposes the motion between the object and the fluid

• This drag force is often from air resistance
• Viscous drag is calculated using Stoke’s Law:

• Where
  • F_d = viscous drag force (N)
  • η = fluid viscosity (N s m⁻² or Pa s)
  • r = radius of the sphere (m)
  • v = velocity of the sphere through the fluid (ms⁻¹)

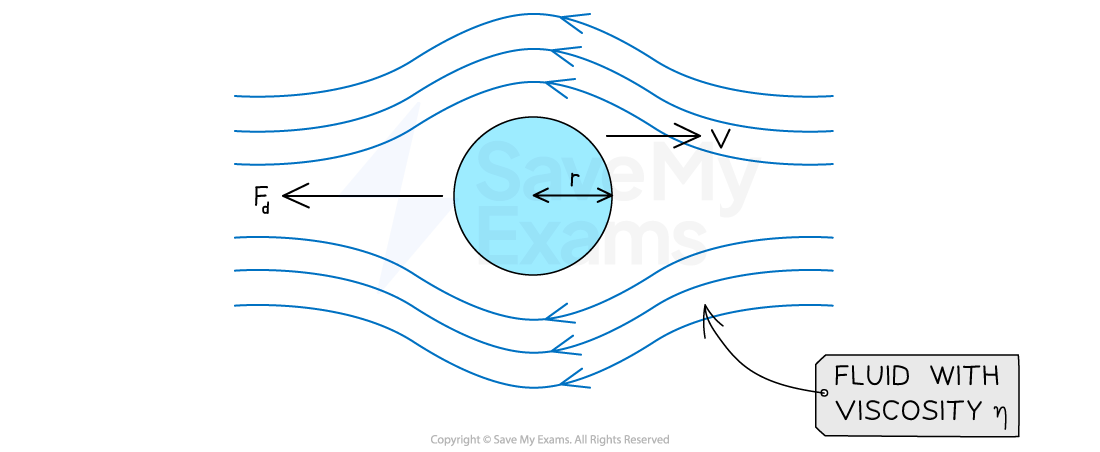
A sphere travelling through air will experience a drag force that depends on its radius, velocity and the viscosity of the liquid

• The viscosity of a fluid can be thought of as its thickness, or how much it resists flowing
  • Fluids with low viscosity are easy to pour, while those with high viscosity are difficult to pour

Water has a lower viscosity than ketchup as it is easier to pour and flow

• The coefficient of viscosity is a property of the fluid (at a given temperature) that indicates how much it will resist flow
  • The rate of flow of a fluid is inversely proportional to the coefficient of viscosity
• The size of the force depends on the:
  • Speed of the object
  • Size of the object
  • Shape of the object