Centripetal Force (SL IB Physics)

• Velocity and acceleration  are both vector  quantities
• An object in uniform circular motion is continuously changing direction, and therefore is constantly changing velocity
  • The object must therefore be accelerating

• This is called the centripetal acceleration and is perpendicular to the direction of the linear speed
  • Centripetal means it acts towards the centre of the circular path

• From Newton's second law, this must mean there is a resultant force acting upon it
  • This is known as the centripetal force and is what keeps the object moving in a circle
  • This means the object changes direction even if its magnitude of velocity remains constant

• The centripetal force (F) is defined as:

The resultant force perpendicular to the velocity required to keep a body in a uniform circular motion which acts towards the centre of the circle

 

•  The magnitude of the centripetal force F can be calculated using:

 

• Where:
  • F = centripetal force (N)
  • v = linear speed (m s⁻¹)
  • ⍵ = angular speed (rad s⁻¹)
  • r = radius of the orbit (m)

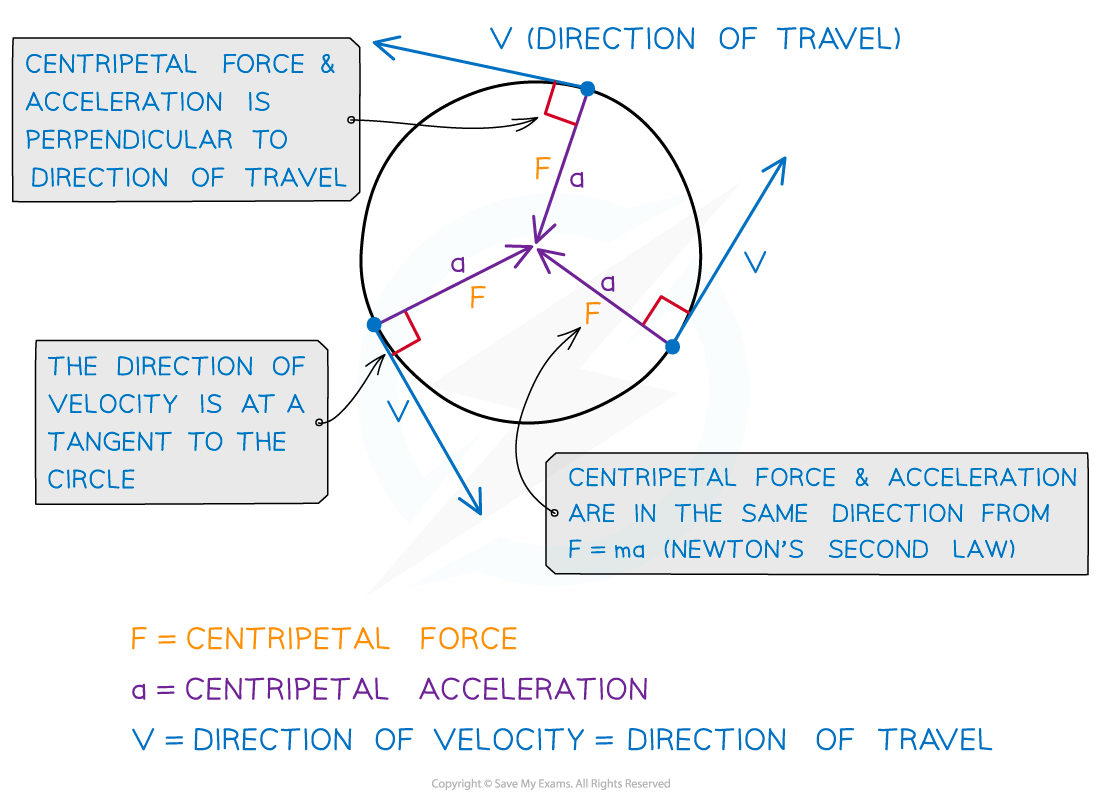
Centripetal force is always perpendicular to the linear velocity (i.e, the direction of travel)

• The direction of the centripetal force is:
  • In the same direction as the centripetal acceleration (towards the centre of the circle) 
    • This is due to Newton's Second Law
  • Perpendicular to the linear velocity

• The centripetal force is not a separate force of its own
• It can be any type of force, depending on the situation, which keeps an object moving in a circular path
  • For example, tension, friction, gravitational, electrostatic or magnetic

Examples of centripetal force

• When solving circular motion problems involving one of these forces, the equation for centripetal force can be equated to the relevant force equation
• For example, for a mass orbiting a planet in a circular path, the centripetal force is provided by the gravitational force

• When an object travels in circular motion, there is no work done
  • This is because there is no change in kinetic energy

Horizontal Circular Motion

• An example of horizontal circular motion is a vehicle driving on a curved road
• The forces acting on the vehicle are:
  • The friction between the tyres and the road
  • The weight of the vehicle downwards

• In this case, the centripetal force required to make this turn is provided by the frictional force
  • This is because the force of friction acts towards the centre of the circular path

• Since the centripetal force is provided by the force of friction, the following equation can be written:

• Where:
  • m = mass of the vehicle (kg)
  • v = speed of the vehicle (m s^–1)
  • r = radius of the circular path (m)
  • μ = static coefficient of friction
  • g = acceleration due to gravity (m s^–2)

• Rearranging this equation for v gives:

 

•  This expression gives the maximum speed at which the vehicle can travel around the curved road without skidding
  • If the speed exceeds this, then the vehicle is likely to skid
  • This is because the centripetal force required to keep the car in a circular path could not be provided by friction, as it would be too large

The frictional force provides the centripetal force

• Therefore, in order for a vehicle to avoid skidding on a curved road of radius r, its speed must satisfy the equation

• A mass attached to a string rotating around is another example of horizontal circular motion

• In this case, the tension is the centripetal force as it acts towards the centre of the circle

• This time, the weight of the mass will be acting as well as the tension of the string

A mass attached to a string will have its weight acting meaning the string is at an angle

• The weight mg of the mass needs to be balanced by the vertical component of the tension

 

• This means the string will always be at an angle and never perfectly horizontal
• The ball's linear velocity, v is still perpendicular to the tension and its weight, mg points downward
• All three forces are perpendicular to each other, so no other component contributes to the centripetal force, just the tension
• The centripetal force is still towards the centre of the circle, but now is just the horizontal component of the tension

• This is an important example of resolving vectors properly. The vertical component does not always have 'sinθ', it depends on what θ is defined as

Banking

• A banked road, or track, is a curved surface where the outer edge is raised higher than the inner edge
  • The purpose of this is to make it safer for vehicles to travel on the curved road, or track, at a reasonable speed without skidding

• When a road is banked, the centripetal force no longer depends on the friction between the tyres and the road
• Instead, the centripetal force depends solely on the horizontal component of the normal force

During banking, the horizontal component of the normal reaction force provides the centripetal force