Energy Released in Fusion Reactions (DP IB Physics): Revision Note
Energy Released in Fusion Reactions
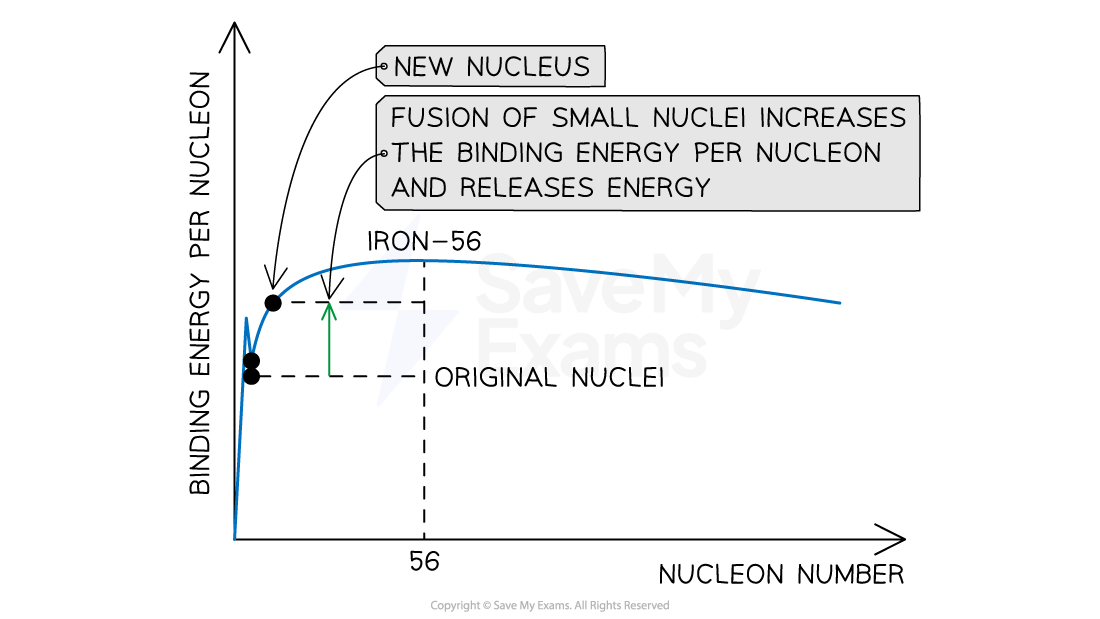
When two small nuclei undergo fusion, the larger nucleus produced as a result will have a higher binding energy per nucleon than the original two nuclei
There is a mass defect between the original nuclei and the new nucleus
Energy is released as a result of the difference in binding energy
For example, when two deuterium nuclei
fuse into one helium nucleus
the binding energy of a helium nucleus is about 28 MeV
the total binding energy of the deuterium nuclei is about 4 MeV
the energy released is 28 - 4 = 24 MeV
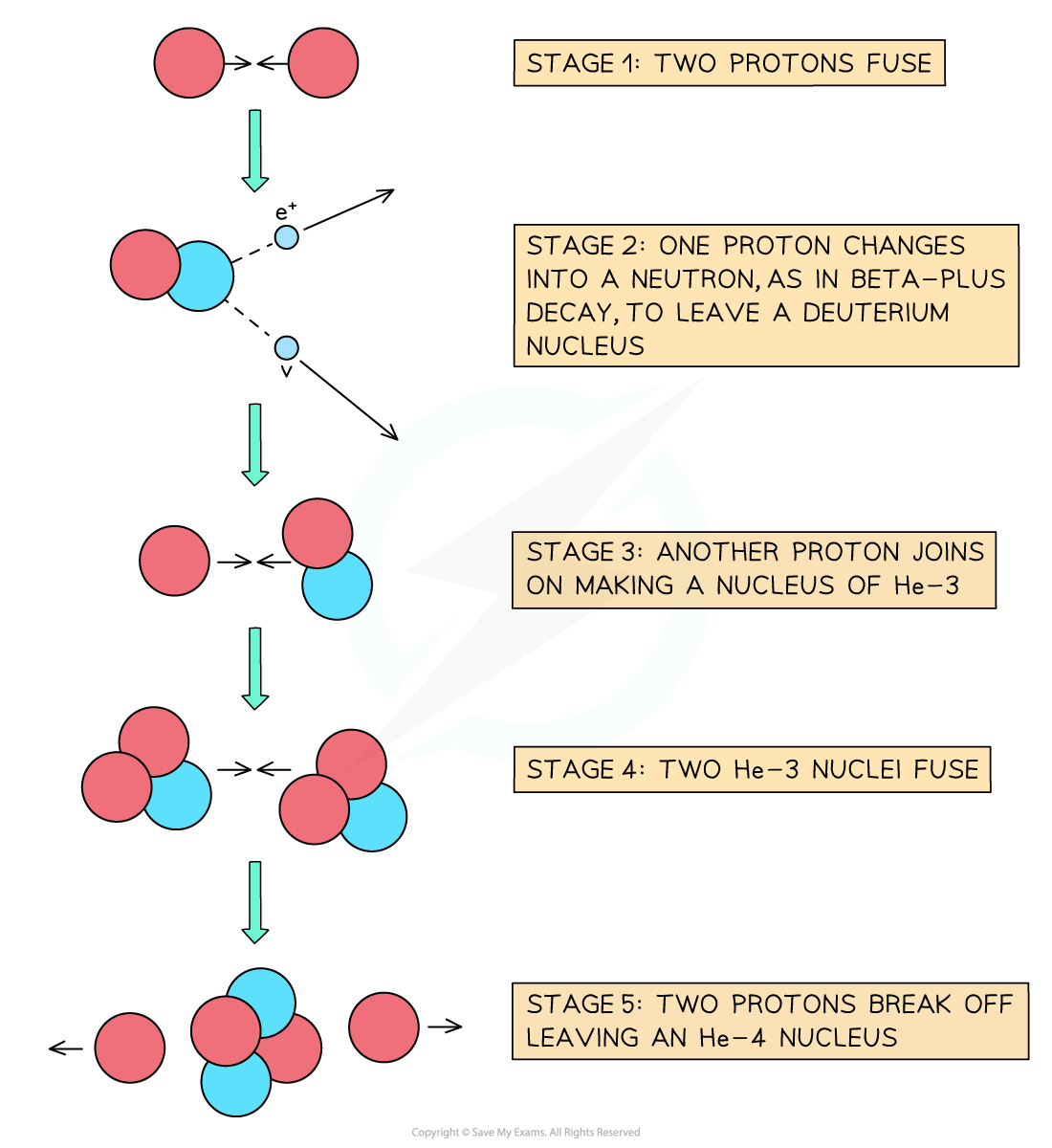
In the hot core of a star, fusion begins with two protons combining to form a deuterium nucleus
The deuterium nuclei go on to form a helium nucleus, plus the release of energy
This provides fuel for the star to continue burning
The proton-proton chain
Worked Example
In the Sun, fusion occurs via a process known as the proton-proton chain.
It is predicted that 80% of the total power output of the Sun is produced through the following cycle:
(overall reaction)
nucleus | rest mass / u |
hydrogen-1 | 1.007825 |
helium-4 | 4.002603 |
The neutrinos produced in the first step carry away 2% of the energy released by the process.
Determine the mass of hydrogen-1 that must be fused each second to produce this output.
Luminosity of the Sun = 3.85 × 1026 W.
Answer:
Step 1: Determine the energy released per overall fusion reaction
In the overall reaction, 4 hydrogen-1 nuclei fuse into a helium-4 nucleus, so the mass defect is:
= 4(1.007825u) − 4.002603u
= 0.028697u
Where atomic mass unit, u = 1.66 × 10−27 kg
Using mass-energy equivalence, the energy released by one reaction is:
= 0.028697 × (1.66 × 10−27) × (3 × 108)2
= 4.287 × 10−12 J
Step 2: Determine the energy released minus the energy that is carried away by neutrinos
Per reaction, neutrinos carry away 2% of 4.287 × 10−12 J, so 98% of the energy contributes to the luminosity of the Sun
= 0.98 × (4.287 × 10−12) = 4.201 × 10−12 J
Step 3: Determine the number of fusion reactions that happen each second
This process accounts for 80% of the luminosity of the Sun,
So, the total power output of the reaction = 0.8 × (3.85 × 1026) W
The number of fusion reactions each second is:
number of reactions =
number of reactions = = 7.332 × 1037 s−1
Step 4: Determine the mass of hydrogen that fuses each second
Every reaction fuses 4 hydrogen-1 nuclei, so the mass per reaction is 4 × 1.007825u
The mass of hydrogen-1 that fuses each second in this process is
mass of hydrogen-1 = 4u × number of reactions
mass of hydrogen-1 = 4 × 1.007825 × (1.66 × 10−27) × (7.332 × 1037)
mass of hydrogen-1 = 4.91 × 1011 kg s−1

Unlock more, it's free!
Did this page help you?