Revision NotesExam QuestionsFlashcards
IBPhysicsSLRevision NotesNuclear & Quantum PhysicsFissionEnergy Released in Fission Reactions

Syllabus Edition

First teaching 2023

First exams 2025

|

Energy Released in Fission Reactions (SL IB Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Energy Released in Fission Reactions

  • When a large (parent) nucleus, such as uranium-235, undergoes a fission reaction, the daughter nuclei produced as a result will have a higher binding energy per nucleon than the parent nucleus
  • As a result of the mass defect between the parent nucleus and the daughter nuclei, energy is released

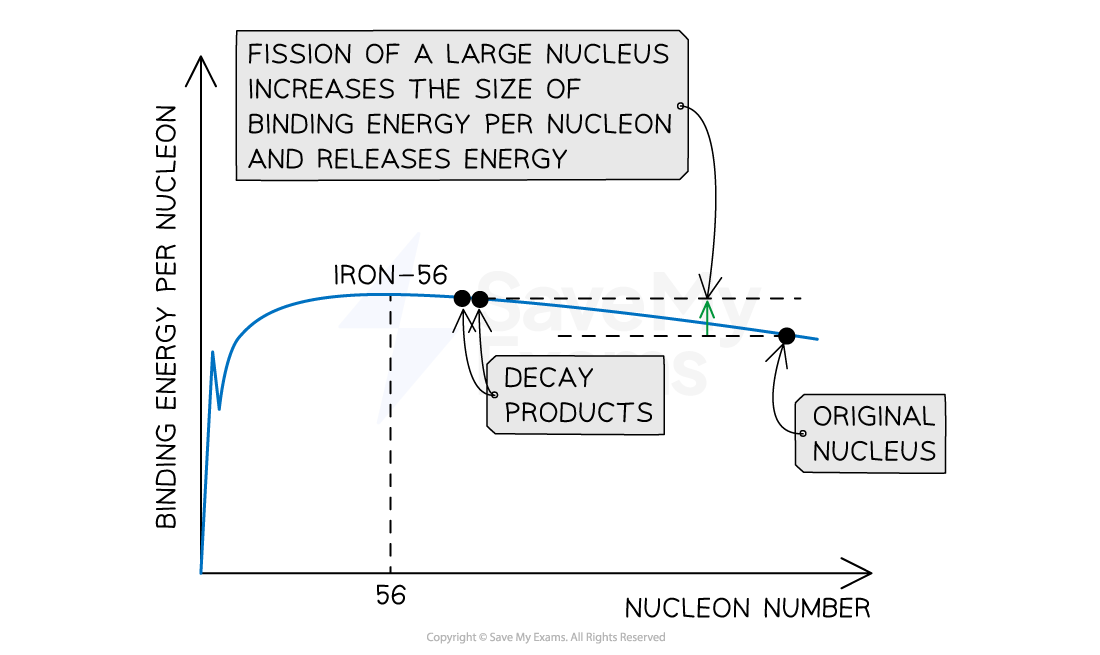
5-4-2-energy-released-in-fission-reactions-graph

Energy can be extracted from fission reactions due to the mass defect between parent and daughter nuclei

  • Nuclear fission is well-regarded as having the fuel source with the highest energy density of any fuel that is currently available to us (until fusion reactions become feasible)

Examples of Common Fuels: Energy Density and Specific Energy Table

8-1-1-energy-comparison-table_sl-physics-rn

  • Calculations involving energy released in fission reactions often require the use of equations found in an array of previous topics, such as

d e n s i t y space open parentheses k g space m to the power of negative 3 end exponent close parentheses space equals space fraction numerator e n e r g y space d e n s i t y space open parentheses J space m to the power of negative 3 end exponent close parentheses over denominator s p e c i f i c space e n e r g y space open parentheses J space k g to the power of negative 1 end exponent close parentheses end fraction

n o. space o f space a t o m s space equals space fraction numerator m a s s space open parentheses g close parentheses space cross times space A v o g a d r o apostrophe s space n u m b e r space N subscript A space open parentheses m o l to the power of negative 1 end exponent close parentheses over denominator m o l a r space m a s s space open parentheses g space m o l to the power of negative 1 end exponent close parentheses end fraction

Worked example

When a uranium-235 nucleus absorbs a slow-moving neutron and undergoes a fission reaction, one possible pair of fission fragments is technetium-112 and indium-122.

The equation for this process, and the binding energy per nucleon for each isotope, are shown below.

straight U presubscript 92 presuperscript 235 space plus space straight n presubscript 0 presuperscript 1 space rightwards arrow space Tc presubscript 43 presuperscript 112 space plus space In presubscript 49 presuperscript 122 space plus thin space 2 straight n presubscript 0 presuperscript 1

nucleus binding energy per nucleon / MeV
straight U presubscript 92 presuperscript 235 7.59
Tc presubscript 43 presuperscript 112 8.36
In presubscript 49 presuperscript 122 8.51

 

(a)
Calculate the energy released per fission of uranium-235, in MeV.
(b)
Determine the mass of uranium-235 required per day to run a 500 MW power plant at 35% efficiency.
(c)
The specific energy of coal is approximately 35 MJ kg−1.
 
For the same power plant, estimate the ratio 
 

fraction numerator m a s s space o f space c o a l space r e q u i r e d space p e r space d a y over denominator m a s s space o f space to the power of 235 U space r e q u i r e d space p e r space d a y end fraction


Answer:

(a)  Energy released per fission of uranium-235

Step 1: Determine the binding energies of the nuclei before and after the reaction

  • Binding energy is equal to binding energy per nucleon × mass number
  • Binding energy before open parentheses straight U presubscript blank presuperscript 235 close parentheses = 235 × 7.59 = 1784 MeV
  • Binding energy after open parentheses Tc presubscript blank presuperscript 112 space plus space In presubscript blank presuperscript 122 close parentheses = (112 × 8.36) + (122 × 8.51) = 1975 MeV

Step 2: Find the difference to obtain the energy released per fission reaction

  • Therefore, the energy released per fission = 1975 – 1784 = 191 MeV

(b)  Mass of uranium-235 required per day

Step 1: List the known quantities

  • Avogadro's number, NA = 6.02 × 1023 mol−1
  • Molar mass of U-235, mr = 235 g mol−1
  • Power output, Pout = 500 MW = 500 × 106 J s−1
  • Efficiency, e = 35% = 0.35
  • Time, t = 1 day = 60 × 60 × 24 = 86 400 s

Step 2: Determine the number of atoms in 1 kg of U-235

  • There are NA (Avogadro’s number) atoms in 1 mol of U-235, which is equal to a mass of 235 g

number of atoms = fraction numerator m a s s space open parentheses g close parentheses cross times N subscript A space open parentheses m o l to the power of negative 1 end exponent close parentheses over denominator m subscript r space open parentheses g space m o l to the power of negative 1 end exponent close parentheses end fraction

  • A mass of 1 kg (1000 g) of U-235 contains fraction numerator 1000 space cross times space open parentheses 6.02 cross times 10 to the power of 23 close parentheses over denominator 235 end fraction = 2.562 × 1024 atoms kg−1

Step 3: Determine the specific energy of U-235

  • Specific energy of U-235 = total amount of energy released by 1 kg of U-235
  • Specific energy of U-235 = (number of atoms per kg) × (energy released per atom) = energy released per kg
  • Energy released per atom of U-235 = 191 MeV
  • Therefore, specific energy of U-235 = (2.562 × 1024) × 191 = 4.893 × 1026 MeV kg−1
  • To convert 1 MeV = 106 × (1.6 × 10−19) J
  • Specific energy of U-235 = (4.893 × 1026) × 106 × (1.6 × 10−19) = 7.83 × 1013 J kg−1

Step 4: Use the relationship between power, energy and efficiency to determine the mass

  • The input power required is:

efficiency & power:  e space equals space P subscript o u t end subscript over P subscript i n end subscript space space space space space rightwards double arrow space space space space space P subscript i n end subscript space equals space P subscript o u t end subscript over e

input power:  P subscript i n end subscript space equals space fraction numerator 500 over denominator 0.35 end fraction space equals space 1429 space MW

input power:  P subscript i n end subscript space equals space E subscript i n end subscript over t space equals space 1429 space cross times 10 to the power of 6 space straight J thin space straight s to the power of negative 1 end exponent

  • Therefore, the mass of U-235 required in a day is:

m a s s space o f space to the power of 235 U space open parentheses k g space s to the power of negative 1 end exponent close parentheses space equals space fraction numerator E subscript i n end subscript space open parentheses J close parentheses over denominator 1 space s end fraction cross times fraction numerator 1 space k g over denominator s p e c i f i c space e n e r g y space o f space to the power of 235 U space open parentheses J close parentheses end fraction

mass of U-235 (per second) = fraction numerator 1429 cross times 10 to the power of 6 over denominator 1 end fraction cross times fraction numerator 1 over denominator 7.83 cross times 10 to the power of 13 end fraction space equals space 1.82 space cross times space 10 to the power of negative 5 end exponent space kg space straight s to the power of negative 1 end exponent

mass of U-235 (per day) = (1.82 × 10−5) × 86 400 = 1.58 kg

  • Therefore, 1.58 kg of uranium-235 is required per day to run a 500 MW power plant at 35% efficiency 

(c)  Ratio of the masses of coal and U-235

  • Since specific energyproportional to space fraction numerator 1 over denominator m a s s end fraction

fraction numerator s p e c i f i c space e n e r g y space o f space to the power of 235 U over denominator s p e c i f i c space e n e r g y space o f space c o a l end fraction space proportional to space fraction numerator m a s s space o f space c o a l space r e q u i r e d space p e r space d a y over denominator m a s s space o f space to the power of 235 U space r e q u i r e d space p e r space d a y end fraction

  • Where the energy density of coal = 35 MJ kg−1

fraction numerator m a s s space o f space c o a l space r e q u i r e d space p e r space d a y over denominator m a s s space o f space to the power of 235 U space r e q u i r e d space p e r space d a y end fraction space equals space fraction numerator 7.83 cross times 10 to the power of 13 over denominator 35 cross times 10 to the power of 6 end fraction space equals space 2.24 space cross times space 10 to the power of 6

  • Over 2 million times (~3.5 × 106 kg) more coal is required than uranium-235 to achieve the same power output in a day (or second, or month or year)

Examiner Tip

If you need to brush up on binding energy calculations, take a look at the Mass Defect & Nuclear Binding Energy revision notes.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Spontaneous & Induced FissionNext:Chain Reactions from Fission
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.