Kepler's Laws of Planetary Motion

Kepler's First Law

Kepler's First Law describes the shape of planetary orbits
It states:

The orbit of a planet is an ellipse, with the Sun at one of the two foci

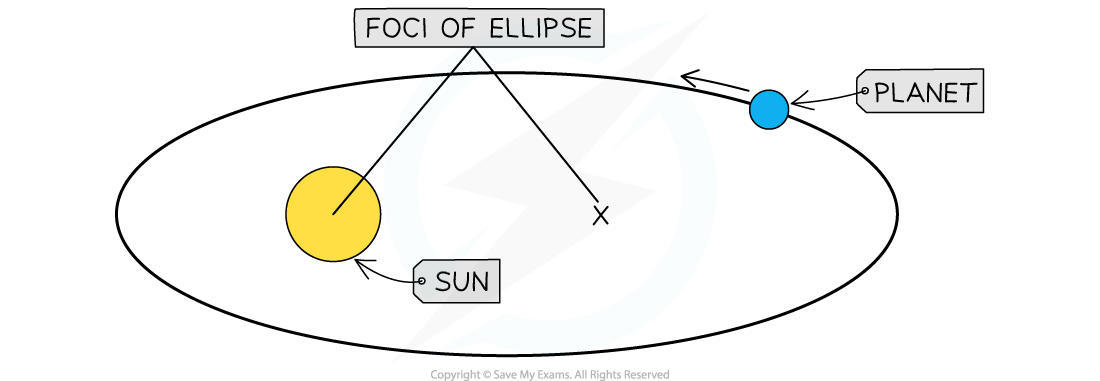
The orbit of all planets are elliptical, and with the Sun at one focus

An ellipse is just a 'squashed' circle
- Some planets, like Pluto, have highly elliptical orbits around the Sun
- Other planets, like Earth, have near circular orbits around the Sun

Kepler's Second Law

Kepler's Second Law describes the motion of all planets around the Sun
It states:

A line segment joining the Sun to a planet sweeps out equal areas in equal time intervals

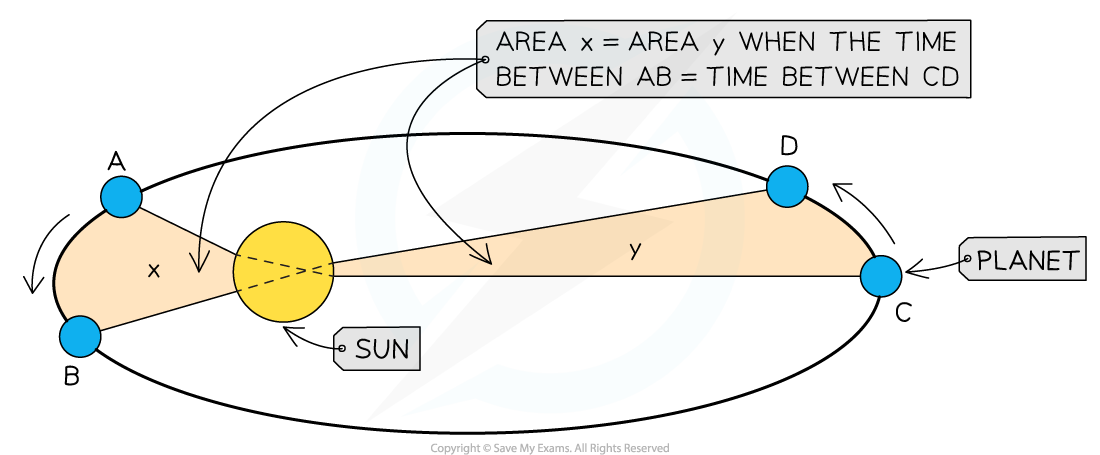
The consequence of Kepler's Second Law is that planets move faster nearer the Sun and slower further away from it

Kepler's Third Law

Kepler's Third Law states

For planets or satellites in a circular orbit about the same central body, the square of the time period is proportional to the cube of the radius of the orbit

This law describes the relationship between the time of an orbit and its radius

$T^{2} \propto r^{3}$

Where:
- T = orbital time period (s)
- r = mean orbital radius (m)

Time Period & Orbital Radius Relation

Since a planet or a satellite is travelling in circular motion when in order, its orbital time period T to travel the circumference of the orbit 2πr, the linear speed v is:

$v = \frac{2 π r}{T}$

This is a result of the well-known equation, speed = distance / time and first introduced in the circular motion topic
Substituting the value of the linear speed v from equating the gravitational and centripetal force into the above equation gives:

$v^{2} = {(\frac{2 π r}{T})}^{2} = \frac{G M}{r}$

Squaring out the brackets and rearranging for T² gives the equation relating the time period T and orbital radius r:

$T^{2} = \frac{4 π^{2} r^{3}}{G M}$

Where:
- T = time period of the orbit (s)
- r = orbital radius (m)
- G = Gravitational Constant
- M = mass of the object being orbited (kg)

The relationship between T and r can be shown using a logarithmic plot

$T^{2} \propto r^{3} \Rightarrow 2 \log T \propto 3 \log r$

The graph of log T in years against log r in AU (astronomical units) for the planets in our solar system is a straight-line graph:

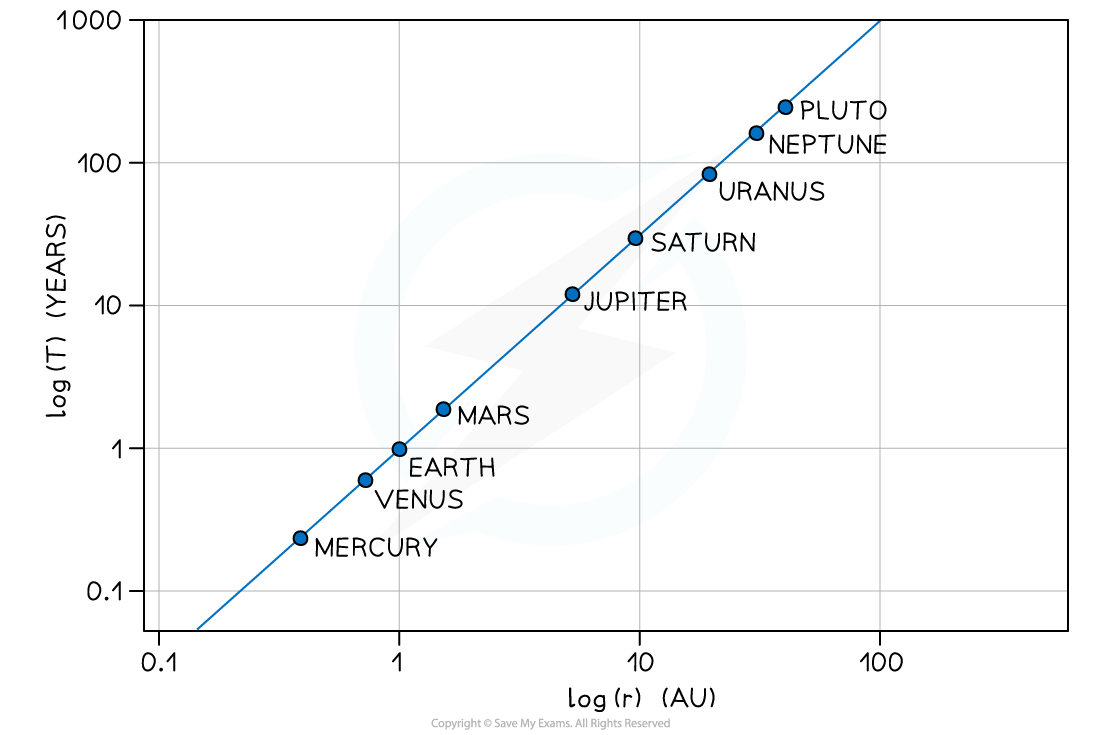
Keplers Third Law Graph, downloadable AS & A Level Physics revision notes

The logarithmic graph of log T against log r gives a straight line

The graph does not go through the origin since it has a negative y-intercept
- Only the graph of log T and log r will produce a straight-line graph, a graph of T vs r would not

Worked example

Planets A and B orbit the same star.

Planet A is located an average distance r from the star. Planet B is located an average distance 6r from the star

What is $\frac{o r b i t a l p e r i o d o f p l a n e t A}{o r b i t a l p e r i o d o f p l a n e t B}$ ?

A. $\frac{1}{\sqrt[3]{6}}$ B. $\frac{1}{\sqrt{6}}$ C. $\frac{1}{\sqrt[3]{6^{2}}}$ D. $\frac{1}{\sqrt{6^{3}}}$

Answer: D

Kepler's third law states $T^{2} \propto r^{3}$
The orbital period of planet A: $T_{A} \propto \sqrt{r^{3}}$
The orbital period of planet B: $T_{B} \propto \sqrt{{(6 r)}^{3}}$
Therefore the ratio is equal to:

$\frac{T_{A}}{T_{B}} = \frac{\sqrt{r^{3}}}{\sqrt{{(6 r)}^{3}}} = \frac{1}{\sqrt{6^{3}}}$

Examiner Tip

You are expected to be able to describe Kepler's Laws of Motion, so make sure you are familiar with how they are worded.

Kepler's Laws of Planetary Motion (SL IB Physics)

Revision Note